高超飞行器内流道激波振荡问题的数值研究及试验验证
2012-04-17郭善广罗世彬
郭善广,柳 军,金 亮,罗世彬
(国防科学技术大学高超声速冲压发动机技术重点实验室,长沙 410073)
0 引 言
超燃冲压发动机是一种新型的推进系统。与火箭发动机相比,超燃冲压发动机能从大气中获取氧气、比冲高;与涡喷发动机相比,超燃冲压发动机内部没有需要冷却的高温转动部件,结构简单,且涡喷发动机不可能达到马赫数6以上。因此超燃冲压发动机成为了高超声速飞行器的首选动力装置[1]。在应用中,超燃冲压发动机需要火箭助推使其达到工作条件。在助推飞行阶段,进气道打开、喷管封闭的高超声速飞行器内流道形成了开口盲腔,盲腔内有可能出现激波振荡现象[2],这对飞行器的结构和飞控系统设计提出严峻挑战。
为消除内流道激波振荡现象,降低助推飞行风险,需要深入研究和分析超燃冲压发动机内流道激波振荡的机理。笔者首先针对典型轴对称吸气式高超声速飞行器,进行了盲腔状态的非定常数值模拟。计算结果表明,其内流道激波振荡现象非常剧烈。其次对该飞行器进行了盲腔状态下的风洞测压和流场观测试验,试验结果验证了数值模拟结果的正确性。
1 数值计算模型
1.1 控制方程和数值方法
论文采用有限体积法进行数值模拟,控制方程为轴对称N-S方程[3]:
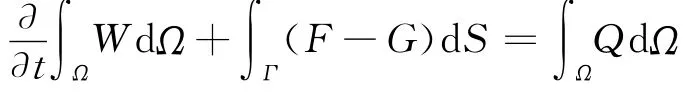
式中W为守恒变量,F和G分别为无粘对流通量和粘性扩散通量,Q为源项。时间域的离散采用“双时间步”方法。无粘对流通量采用二阶AUSM格式进行离散,粘性项采用中心差分格式离散。湍流模型选用k-ωSST模型,补充完全气体状态方程进行数值求解。
1.2 边界条件和初始条件
飞行器壁面采用无滑移绝热壁条件:u=0,v=0,∂T/∂n=0。边界层内∂p/∂n=0。飞行器中轴线采用轴对称边界条件:无流量通过。计算域边界采用压力远场边界条件:u=u∞,v=v∞,T=T∞,p=p∞。
初始化中,压力、温度采用自由来流参数,速度为零。
1.3 飞行器简化模型
典型轴对称吸气式高超声速飞行器采用混合压缩式进气道,外压缩由三级压缩锥组成。环形进气道收缩为中心扩张通道,形成燃烧室和尾喷管。
为便于分析,对飞行器模型做了如下简化:三维流动简化为轴对称流动;不考虑飞行器翼面和进气道支板的影响。在内流道壁面上布置了三个测点:point-1、point-2、point-3,分布在进气道、隔离段和尾喷管附近,用来监测内流道壁面的压力变化。在进气道入口处,布置了一个监测面Inlet。简化后的模型及测点的位置如图1所示。

图1 高超声速飞行器的简化模型Fig.1 A simplified model of the hypersonic vehicle
1.4 计算网格
主要研究高超声速飞行器内流道的激波振荡现象,外流场计算域仅包含进气道唇口下游小部分。整个计算域分成了13个子域。计算采用二维结构化网格。为了适合粘性和激波捕捉的需要,在近壁区和进气道中心锥头部进行了网格加密,壁面附近第一层网格的法向距离为1×10-5m。整个计算域的网格数量为3.5万。尾喷管底部设为壁面。网格及边界条件的给定如图2所示。
2 计算结果及分析
计算条件:来流马赫数为4.92,静压为1908Pa,迎角、侧滑角均为零。
图3给出了飞行器整机阻力系数随时间的变化。图4给出了一个周期内入口监测面平均轴向速度与平均压力随时间的变化。
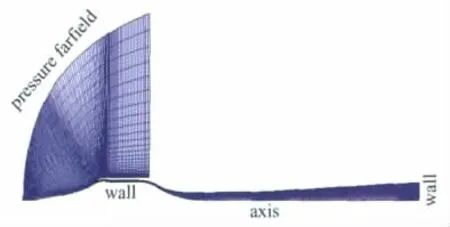
图2 计算网格Fig.2 Computational grid of the vehicle
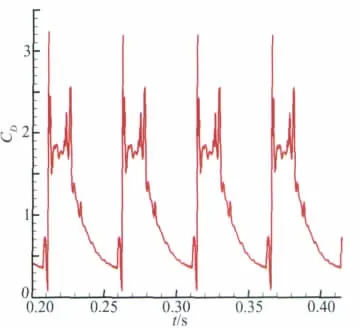
图3 整机阻力系数随时间的变化Fig.3 Drag coefficient-time histories of the vehicle
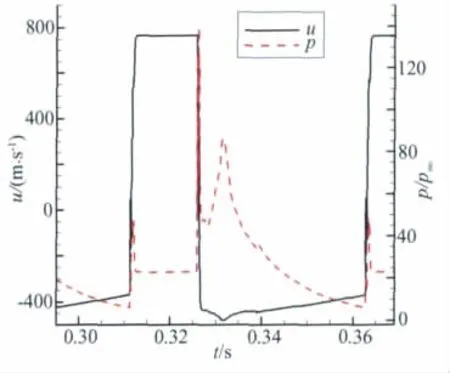
图4 Inlet监测面平均轴向速度与平均压力随时间的变化Fig.4 Average axial velocity-time histories and average static pressure-time histories of inlet during aperiod
从图3中可以看出,飞行器整机阻力振荡非常剧烈,且呈周期性变化趋势,最大阻力是最小阻力的36倍。由图4可以看出,入口速度与压力的变化是一个此消彼长的过程,说明盲腔内的气流振荡实质上是开口系统中压力势能和动能交替转化的过程。
图5给出了一个周期内各典型时刻的流场。图(a)为各典型时刻飞行器内外流场的马赫数等值线和流线图,图(b)为对应时刻的内流道壁面静压的沿程分布。图中p∞为来流静压,cone为中心锥壁面,cowl为内流道上壁面。
下面给出一个振荡周期内,各典型时刻的流场分析:
(1)t=311.4ms时刻,来流被吸入内流道。上个周期中飞行器前体的大弓形激波逐渐附体并被吸入内流道,进气道一级压缩锥面上的激波和二级压缩锥面上的等熵压缩波建立,进气道前部压力升高;
(2)随着激波向内流道下游运动,t=312.6ms时刻,飞行器前体波系建立,进气道启动。激波扫过的区域,压力迅速升高。激波扫过测点2时,测点2的压力升高为56倍的来流静压,激波运动到内流道底部时,完全启动的流场建立;
(3)右向运动的激波与喷管底部壁面相撞,产生高压气体,形成一道反射激波。随着来流在内流道底部的堆积,推动反射激波向上游运动。反射激波扫过后,流体压力升高、速度基本滞止。t=319.3ms时刻,反射激波运动到测点2附近;
(4)t=326.4ms时刻,反射激波运动到唇口附近,唇罩头部的脱体激波前移,此时进气道内的气体质量达到最大。随着内流道压力的饱和,反射激波被推出进气道。反射激波遇开口端反射形成一系列膨胀波,膨胀波向下游运动,唇口处随即形成倒流,压力也迅速下降;
(5)唇口处喷出的高压气体对超声速主流产生的干扰较大,在唇罩前侧形成一道较强的弓形激波。进气道前体斜激波与该弓形激波交汇。随着气体倒流的加剧,燃烧室和尾喷管内的气体相继流出,喷出的气体推动唇罩前侧的弓形激波向前运动。t=330.0ms时刻,弓形激波被推至流场最前侧,中心锥脱体激波与弓形激波合并。内流道的喷流与来流相互作用,在喷流的前后侧形成了两个分离区;

图5 一个周期内各典型时刻流场Fig.5 Flow fields of typical moments in a period
(6)当膨胀波运动到喷管底部时,形成一系列反射膨胀波向上游运动。反射膨胀波扫过的区域压力继续降低。t=363.0ms时刻,膨胀波被推至进气道入口附近,波后压力较低的气体与进气道入口处的高压气体接触,引起压力不平衡,内流道气体得到压力增量,反射出一道压缩波向下游运动。
内流道中压缩波扫过的地方,壁面压力升高,气体向内流道下游运动;内流道中压缩波未扫过的区域,气体仍向唇口方向运动。后面的压缩波不断赶上前面的波,在测点1之前压缩波叠加成一道正激波。一个周期结束,进入下一个周期。
图6给出了一个周期内测点压力随时间的变化。

图6 一个周期内测点压力随时间的变化Fig.6 Static pressure-time histories of survey points in a period
从图6中3个测点的压力变化趋势中,可以看出以下4个特点:
(1)测点位置越靠后,压力振荡的幅度越大。测点1、2和3的压力振幅分别为145p∞、179p∞和190p∞;
(2)测点1、2均出现了3个压力峰值:峰值Ⅰ、Ⅱ和Ⅲ。测点3出现了2个压力的峰值:峰值Ⅰ和Ⅱ;
(3)随着测点位置的后移,峰值Ⅰ、Ⅱ出现的时间依次滞后。测点1的峰值Ⅰ、Ⅱ出现得最早,然后是测点2,最后是测点3;
(4)一个周期内,3/4的时间都在排气,只有1/4的时间为气体在内流的堆积。且气体的吸入与排除二者之间的转换非常迅速。
机理分析:外流气体进入进气道与通道内仍向外流动的气流交汇产生交汇面激波,该激波扫过测点时形成压力峰值Ⅰ,因此该峰值经过各测点的时间依次滞后,且由于交汇面流量的累积,该峰值也依次增大。由测点1、3的峰值Ⅰ之间时间间隔可以得到交汇面激波的传播速度,即进气道吸气流场的特征时间。
交汇面激波后的流场即为内流道启动后的流场,在交汇面激波到达内流道底部时,完全启动的流场建立起来。交汇面激波与内流道底部壁面相遇后,形成反射激波。由于来流在底部的堆积,形成反压,推动反射激波向唇口方向移动,反射激波经过的地方,压强升高。因此测点3的压强经过峰值Ⅰ后率先上升,测点2、1随之升高。
测点2、3的峰值Ⅱ对应反射激波后的反压值,由于反射激波后的流场为亚声速流场,各处压强相差不大,测点2、3的峰值也较为接近。并且在反射激波传播过程中,该压力峰值还具有较宽的范围。
测点1的位置位于唇口附近,在反射激波扫过后,压力爬升,但反射激波马上被推出唇口,反射形成膨胀波,膨胀波向底部运动,唇口处随即形成倒流,压力也迅速下降。由于倒流的开始点与测点1的峰值Ⅱ的节点时间基本相同,因此测点1的峰值较窄,并且唇口处的膨胀波比底部反压更早传到该点,该点峰值Ⅱ还未上升到2、3的水平就下降了。膨胀波向内传播,扫过的地方,气流倒流,压强骤降。因此,由测点1和测点3二者的峰值Ⅱ之间的时间间隔,可以得到膨胀波向内传播的速度,这一值即为进气道排气流场的特征时间。
峰值Ⅲ产生的原因与喘振有关。
进气道吸入气体时,流量不变,对应图4中速度的曲线平台,结合图6中测点1的相应的压力曲线平台可以看出,进气道吸入气体时,入口附近流场一直为稳定的启动流场,所以流率不变,此时,气流速度较大,流率较大;而进气道排出气体时,入口附近流场不断变化,气流速度相对较小,流率较小,因此,进气道的排气时间要大于吸气时间。
3 试验验证
为了验证该计算结果的可信度,有必要将计算结果与试验结果进行对比。试验在南京航空航天大学的暂冲式高超声速风洞中进行。高超声速飞行器尾喷管底部采用堵锥封住,形成盲腔构型试验模型。风洞来流条件:马赫数为4.92,压力为1908Pa,迎角、侧滑角均为零。在试验模型上布置了3个压力测点,其分布位置与计算模型的监测点相同。
图7给出了一个周期各内典型时刻的风洞纹影照片。
从图7可以看出,(a)时刻,飞行器前体波系正常建立,进气道启动。(b)时刻,飞行器前体激波被推至飞行器最前侧,唇口处形成喷流。(c)时刻,飞行器前体激波逐渐附体。(d)时刻,来流再次进入内流道,飞行器前体激波系再次建立,一个周期结束。由以上可知,在前体流场的周期性变化趋势上,计算结果与试验纹影符合较好。

图7 一个周期内各典型时刻的纹影照片Fig.7 Schlieren images of typical moments in a period
图8给出了监测点压力随时间变化的试验数据。
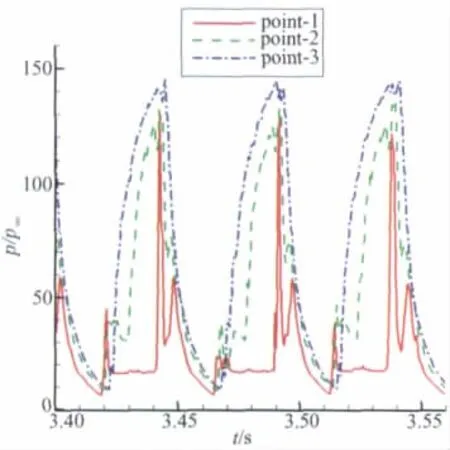
图8 测点压力随时间变化的试验数据Fig.8 Static pressure-time histories of the experiment
由图8可以看出以下3个特征:
(1)试验所得测点压力振荡频率为21.3Hz,与计算的19.3Hz的频率符合较好;
(2)测点1和测点2均出现了3个压力峰值,测点3出现了2个压力峰值。这与计算完全吻合;
(3)随着测点位置的后移,峰值Ⅱ出现的时间依次滞后。这与计算完全吻合。
计算数据与试验结果的不同点在于计算所得测点压力振荡幅度明显大于试验值。试验结束后,发现堵锥被吹离了尾喷管底部,内流道高压气体在后部泄漏,因此造成试验的压力振幅低于计算值。
4 结 论
通过对典型轴对称吸气式高超声速飞行器盲腔流场的研究,可以得到如下结论:
(1)在助推飞行段,吸气式高超声速飞行器内流道会出现激波振荡,并伴随有气流在飞行器内流道“吐出”与“吸入”现象。在计算条件下,激波振荡频率为19.3Hz,内流道壁面压力最大振幅为190倍的来流静压;
(2)一个振荡周期内,3/4的时间为排气时间,1/4的时间为吸气时间,且激波和膨胀波在内流道内往返运动各一次。越靠近内流道底部,壁面压力振荡幅度越高;
(3)计算结果和试验结果吻合较好。计算所得的前体流场变化特征、内流道壁面压力振荡频率和壁面压力变化趋势与试验结果吻合较好。验证了计算结果的可信度;
(4)计算所得壁面压力振荡幅度大于试验结果。原因在于试验过程中,尾喷管底部的堵锥已经被吹开了一部分,导致了高压气体的泄漏,使得测点压力峰值低于计算值。
致谢:感谢南京航空航天大学谭慧俊教授、孙姝副教授提供的风洞试验数据。
[1] MRRCIER Robert,McCLINTON Charles.Hypersonic propulsion-transforming the future of flight[R].AIAA 2003-2732.
[2] 白晓征,刘君,郭正,等.冲压发动机进气道压力振荡过程的数值研究[J].推进技术,2008,29(5):562-565.
[3] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社.
[4] 赵海洋.高精度计算方法研究及应用[D].国防科技大研究生院硕士学位论文,2002.
[5] TAN Hui-jun,SUN Shu.Oscillatory flow of rectangular hypersonic inlet unstart caused by downstream massflow choking[J].Journal of Propulsion and Power,2009,25(1):138-147.
