5000m特大跨度悬索桥空气动力稳定性能理论研究

邵亚会，葛耀君，柯世堂，杨詠昕

（1.合肥工业大学土木与水利工程学院，合肥 230009；2.同济大学土木工程防灾国家重点实验室，上海200092）

0 引 言

二维颤振分析基于片条理论，用广义质量模拟全桥真实状态的质量系统，用节段模型在气动力和自身重力作用下的受力状态和运动方式模拟全桥真实的受力状态，不考虑风荷载和结构的三维效应。为考察三维效应，有必要引入三维桥梁颤振分析。1989年，Agar［1］基于Scanlan的线性自激力模型和颤振分析理论，提出了将颤振问题简化为求解非对称实矩阵的特征值问题，采用双参数搜索迭代求解；Beith也提出了相同的方法［2］。1992年，Namimi［3］提出了颤振分析的PK－F法，同济大学程韶红、张新军等人沿用了此法。1994年，陈政清［4］提出多模态单参数搜索颤振分析方法，将颤振问题转化为求解复矩阵的广义特征值问题，且认为桥梁颤振中高阶模态的参与具有有利与不利双重效果，该方法能方便地求解颤振临界风速和频率，但不能描述颤振发生的全过程。1996年，Jain［5］也将颤振问题转化为求解矩阵特征值问题，侧重于求解特征多项式的实部和虚部方程。1995年，Miyata［6－7］和Yamada首次提出了颤振全模态分析方法，但没有考虑结构阻尼的影响。Dung［8］在1998年发展了该方法，仍无法有效考虑结构阻尼的影响。2000年，葛耀君［9］提出了大跨度桥梁三维颤振分析的全模态方法，考虑了结构阻尼的影响，同时也将颤振频域分析方法提高到了一个新的高度，自此之后关于颤振频域方面的研究多是基于此的细化和延伸。2000年之后，国内外诸多学者继续对大跨度桥梁的颤振问题进行了大量研究［10－13］，通过自主研发软件和嫁接商业软件进行二次开发，丰富了大跨度桥梁三维颤振研究，不同之处在于针对不同的研究对象，考虑了不同的求解过程和技巧。

已有文献多是针对跨度在1500m以下的大跨度悬索桥进行气动稳定性研究，而对于跨度超过1500m，甚至达到5000m的特大跨度悬索桥研究成果较少，可供参考的结论不多。为此，将在已有三维频域全模态颤振分析方法基础上，进行细化和拓展，考虑三方向气动导数的影响、静风荷载非线性的影响、几何非线性的影响、各种风荷载随高度的梯度影响等因素，研究5000m特大跨度悬索桥的三维空气动力稳定性能，并与风洞试验结果和二维颤振分析结果进行对比，从三维颤振稳定、三维静风稳定的角度，进一步论证特大跨度悬索桥在5000m跨度范围的可行性。

1 全模态颤振分析方法

1.1 颤振基本方程

处于风环境中的桥梁结构的动力平衡方程可以表示为：

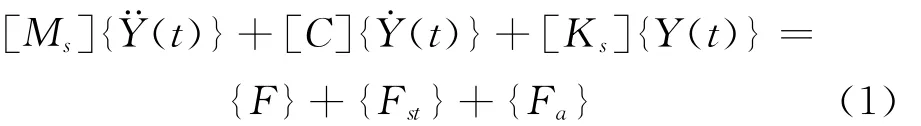
［Ms］结构总体刚度矩阵；［Cs］结构总体阻尼矩阵；［Ks］结构总体刚度矩阵，［Ks］＝［Ke］＋［Kg］，为弹性刚度矩阵和几何刚度矩阵的和；｛F｝自激气动力等效荷载，｛F｝＝｛Fd｝＋｛Fs｝＝［Ca］＋［Ka］｛Y｝；｛Fst｝为静风荷载；｛Fa｝为惯性力；｛Y｝结构位移向量。

在进行颤振分析时，将结构自身重力和静风荷载的作用等效为悬索桥结构的预应力，进行有预应力的模态分析，将各参数带入（1）式后，可以得到：

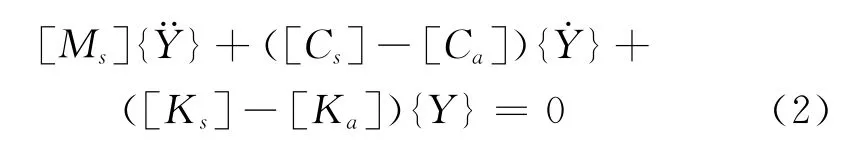
令｛Y｝＝｛φ｝eet，则有：

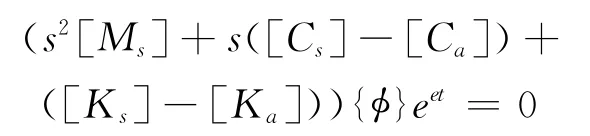
只有当方程左端的矩阵非奇异时方程（2）才具有非平凡解。实际上这就是一个n次特征值问题。求解该方程将得到2n个特征值和对应的特征向量。方程（2）的通解可以表达为2n个解的叠加：

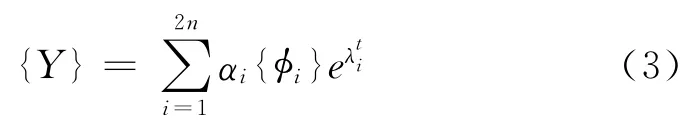
对应复共扼特征值对的分量为：

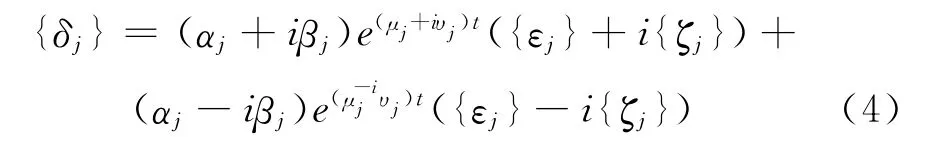
如果所有特征解复共扼成对的，则式（4）可以写成如下形式

式中，当ui为负时表明系统振动收敛。当ui为正时表明系统颤振发散，此时颤振的圆频率为Wj。

1.2 风荷载的处理

Scanlan建立了桥梁结构的分离流扭转颤振理论，建议用6个实函数的颤振导数表示钝体气动自激力的公式。近年来，人们逐渐注意到桥梁断面侧向位移对其气动性能的影响，为此，Sarka和Jones［5］将该气动力模型予以推广，考虑了桥梁断面侧向位移对其气动性能的影响，提出了用18个颤振导数表示的气动力公式。在无风洞试验结果的情况下，按照拟静力理论得到的侧向导数如下［14－16］：

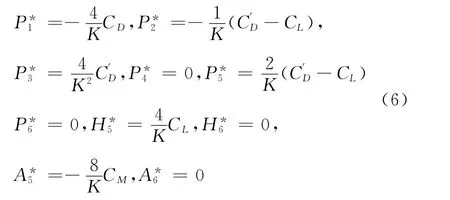
对于缆索气动力，考虑了主缆和吊杆的自激气动力、静风荷载，以及自激气动力和静风荷载随高度的变化，如图1所示。缆索所受的气动力表现为正的气动阻尼，颤振导数只与阻力系数有关，对圆形缆索的阻力系数均取为0.7，缆索的孔隙率取为20%，即在缆索净截面面积的基础上考虑20%的面积放大系数。

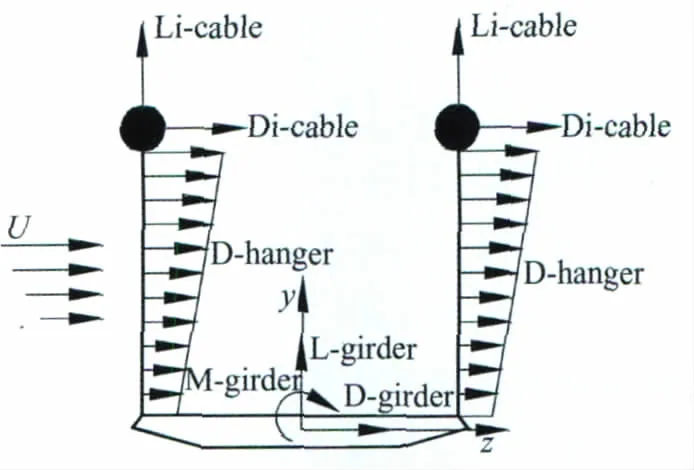
图1 缆索和吊杆风荷载示意图Fig.1 Wind loads on cable and hangers

结构阻尼的处理，按照经典瑞利阻尼来考虑，如式（7～8）所示。

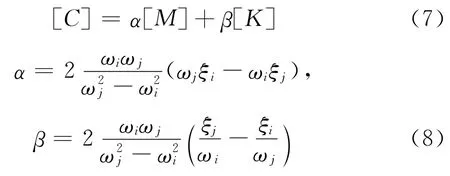
其中，［C］为结构阻尼矩阵，［M］为结构质量矩阵，［K］为结构刚度矩阵，α、β分别为瑞利阻尼系数；ωi、ωj分别为结构第i阶和第j阶振动圆频率，ξi、ξj分别为结构第i阶和第j阶振动阻尼比。

基于上述颤振基本方程和风荷载处理方式，实现了特大跨度悬索桥三维频域颤振的全模态分析方法。该方法有以下重要特点：（1）可以同时考虑竖向导数、侧向导数和扭转向导数对颤振的影响。侧向导数的取值法则如前文所示，按照准定常原则取值。（2）可以同时考虑加劲梁和缆索系统的静风荷载，并考虑风荷载随高度变化的梯度变化。（3）精细化地考虑了主缆和加劲梁吊杆的自激力和静风荷载，主缆和吊杆的受力面积按照毛截面面积取值，主缆的孔隙率为20%。（4）可以同时考虑特大跨度悬索桥的几何非线性，静风荷载的非线性。

2 5000m悬索桥颤振性能分析

2.1 颤振风速与频率

采用三维全桥全模态频域颤振分析方法，和风洞试验识别的颤振导数以及三分力系数，对两种加劲梁方案的特大跨度悬索桥进行了三维全桥颤振分析，每种方案各计算了4种矢跨比的分方案。以窄开槽方案为例，主要分析结果如表1所示，需要说明的是风洞试验表明，上稳定板的颤振控制效果最好，这里只给出此方案的三维分析结果。颤振计算过程中考虑的主要因素包括：（1）竖向导数、侧向导数和扭转向导数；（2）加劲梁和缆索系统的静风荷载，并考虑风荷载随高度变化的梯度变化，以及由静风荷载引起的初始迎角；（3）加劲梁和缆索系统的自激力荷载；（4）颤振导数随风迎角的非线性变化；（5）分别搜索了加劲梁正对称和反对称扭转颤振的颤振临界风速和颤振形态，以期对特大跨度悬索桥的颤振性能有更为全面的认识和把握。

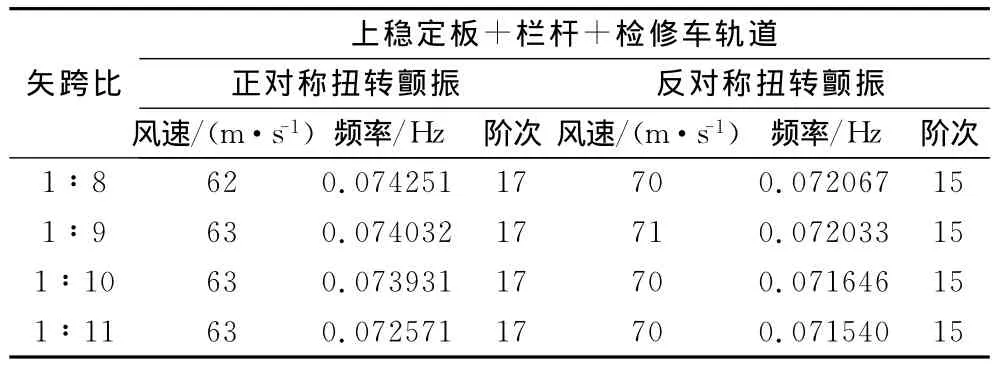
表1 窄开槽方案三维颤振分析结果Table 1 Three dimensional flutter analysis for narrow slotted scheme

研究发现：

（1）对于上水平稳定板、防撞护栏和检修车轨道组合方案的窄开槽加劲梁悬索桥方案，加劲梁正对称扭转颤振的临界风速为63m／s，反对称扭转颤振临界风速为70m／s，与矢跨比无明显关系。

（2）颤振频率随矢跨比减小而降低，这与二维颤振分析的结论一致；反对称扭转颤振频率均低于同矢跨比的正对称扭转颤振频率；正对称扭转颤振发生的模态均为第17阶复模态，反对称扭转颤振发生的模态为第15阶复模态，与矢跨比无关。

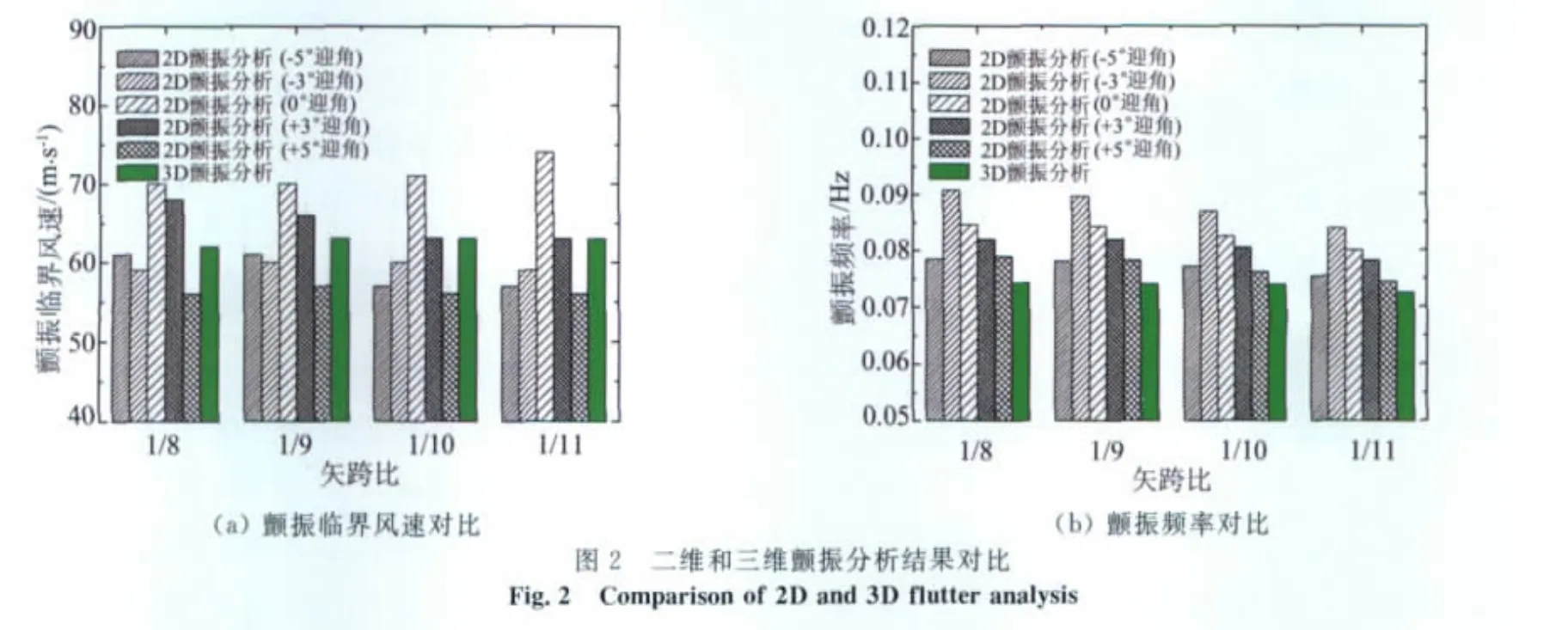
（3）二维和三维颤振分析结果的对比发现，如图2所示，二维颤振分析在不同迎角时的颤振临界风速和频率离散度较大，三维颤振分析中自动考虑了静风引起的附加迎角的变化，其颤振临界风速大于60m／s，0°迎角时的二维颤振临界风速与三维颤振临界风速较接近。

（4）风洞试验、二维和三维颤振分析结果均证明矢跨比对颤振分析结果的影响较小，因此在设计跨度为5000m的悬索桥时，不必刻意选择矢跨比。

同理，研究证明宽开槽加劲梁方案的颤振临界风速均大于80m／s，颤振形态的变化规律与窄开槽方案类似，在此不详述。

2.2 颤振形态

图3为窄开槽方案三维全桥颤振分析获得的颤振形态，以矢跨比1∶10和1∶11为例，其余矢跨比的颤振形态与其相似，在此予以省略。

研究发现：

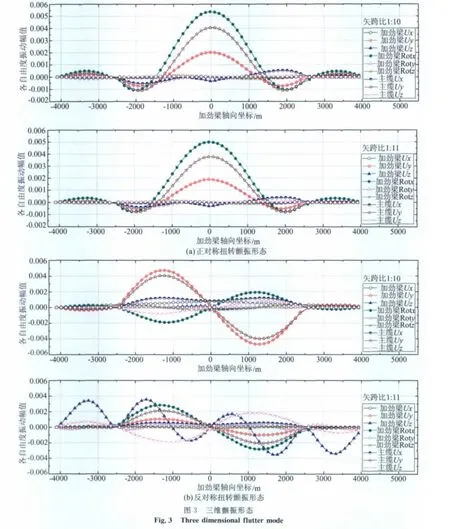
（1）颤振形态：最先出现的颤振形态均为加劲梁第一阶正对称扭转为主、竖弯向自由度强烈参与的颤振形态，加劲梁侧向振动参与程度较小，反对称扭转颤振晚于正对称扭转颤振出现，这种现象与矢跨比的变化无关。

（2）反对称扭转颤振形态：反对称扭转颤振形态以加劲梁的第一阶反对称扭转振动为主，矢跨比为1∶8，1∶9，1∶10时，主要参与的竖向振动为加劲梁第一阶反对称竖弯振动，矢跨比为1∶11时，主要参与的竖向振动为加劲梁第二阶反对称竖弯振动。

（3）主缆振动形态：颤振临界状态时，主缆的竖向振动幅值远大于加劲梁，说明对于特大跨度悬索桥，主缆的振动幅值很大，需要引起注意。另外，主缆沿桥梁轴向振动的幅值也较大。

3 二维和三维颤振分析结果的解释

通过对特大跨度悬索桥二维和三维颤振分析的对比研究，不难发现无论从颤振临界风速还是颤振频率来看，5000m特大跨度悬索桥的二维和三维颤振分析结果相差均较小，有较大程度的可比性，这有悖于人们对于特大跨度悬索桥的传统认识。这种现象可以从以下几个角度来解释：

（1）三维颤振临界状态时，加劲梁的颤振形态是以扭转为主的耦合颤振，竖弯振动在颤振运动中有较大程度的参与，加劲梁的侧向振动模态虽然也参与了颤振运动，但是参与程度较小，不是导致颤振发散的主要模态。而二维颤振临界状态时，也是以加劲梁的扭转为主的耦合颤振，竖向自由度参与较为强烈。从这点来看，两者是统一的，只不过对于三维颤振分析，还有其它高阶模态参与进来，高阶模态的参与会有正负效应，可能会升高或者降低颤振临界风速值。

（2）三维颤振分析时，计入了缆索系统的荷载，包括自激力和静风荷载，且考虑了这些荷载沿着高度的梯度变化。计入缆索系统的风荷载相当于增加了系统的气动阻尼，可以提高颤振临界风速和降低颤振频率，据已有文献记载，江阴大桥颤振临界风速可以提高0.8%。

（3）三维颤振分析时，考虑了缆索系统的振型，这可以提高颤振临界风速，索横弦向位移的参与，减小了颤振振型中主梁扭转位移的比重，使桥梁吸收气动阻尼的能力增加，而吸收气动负阻尼的能力降低。这种因素导致悬索桥颤振临界风速提高，但是效果不明显。

（4）三维颤振分析时，考虑了侧向导数的影响，虽然只是按照拟静力理论来拟合的侧向气动导数，但在一定程度上反映了侧向导数对特大跨度悬索桥颤振性能的影响。有研究表明［16－17］，侧向导数对某些加劲梁断面的悬索桥有较大的影响。而在二维颤振分析中，没有考虑侧向导数的这种影响，这导致了二维和三维颤振分析结果的差异。

4 动力和静力稳定性能的关系

三维静风稳定性能分析主要考虑气动力非线性、结构几何非线性和材料非线性。随风速的增大，悬索桥自身风荷载呈非线性增长，悬索桥整体刚度不断发生变化；而当风速不变时，由于振动姿态（风迎角、迎风面积）的变化，导致结构构件的静风力、力矩、位移等沿桥梁轴线不均匀分布，也会导致结构的风荷载和刚度发生变化，带来风荷载的非线性变化，即气动力的非线性效应。几何非线性表示结构有大变形发生，荷载和位移不服从线性关系，刚度矩阵在求解过程中不断发生变化，不是固定的。悬索桥具有明显的几何非线性特征：首先悬索桥的主缆为几何可变体系，主要依靠自重和加劲梁恒载获得结构刚度以抵抗变形，缆索受力状态表现出明显的几何非线性性质；其次悬索桥的加劲梁相对纤细和轻柔，结构在外荷载的作用下较易产生大变形，整体平衡方程不是基于初始平衡位置建立，而是应基于变形后的位置建立；长大的悬索桥主缆同时具有垂度效应，这也带来了悬索桥的几何非线性。随着悬索桥跨度的不断增加，其几何非线性效应必将越来越显著。材料非线性就是材料的本构关系不是线性的，按照钢材的理想弹塑性曲线进行计算输入。按照杆系结构的空间稳定理论，悬索桥结构静力失稳的问题可以表述为下述三重非线性（几何、材料和风荷载）方程［18］：

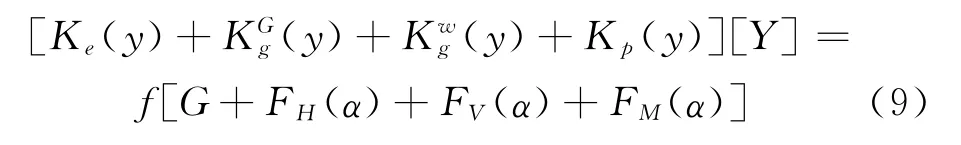
其中：

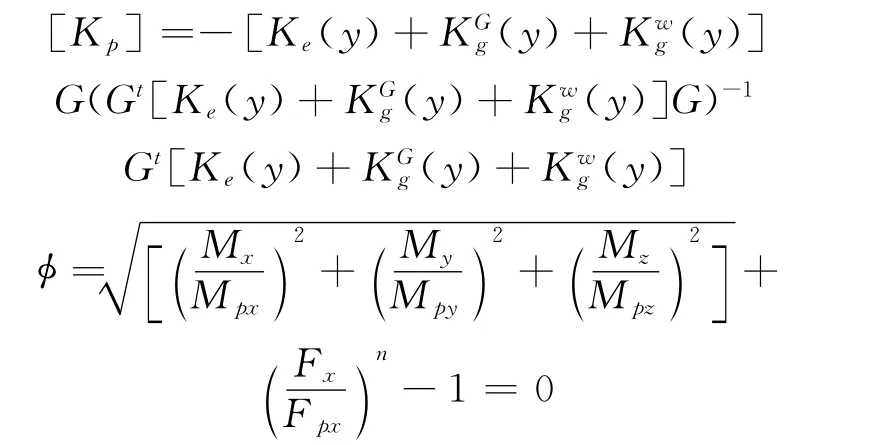
［Ke］为结构弹性刚度矩阵；［］为重力引起的结构几何刚度矩阵；［］为风荷载引起的结构附加几何刚度矩阵；［Kp］为结构塑性刚度矩阵；G为结构屈服面上的梯度矩阵；Mi为屈服面上的弯矩；Fi为轴向塑性力。

为研究5000m超大跨度悬索桥方案的静风稳定性能，对两种加劲梁方案的悬索桥分别进行了矢跨比为1∶8、1∶9、1∶10、1∶11的三维三重非线性静风稳定全过程仿真模拟。计算获得的静风失稳临界风速如图4所示，并与三维颤振分析获得的颤振临界风速相互对比，研究发现：5000m特大跨度悬索桥的颤振临界风速小于静风失稳临界风速，空气动力失稳是控制设计的关键因素；对于宽槽加劲梁方案，静力扭转发散临界风速与颤振失稳临界风速大小相当，在同一量级上，对空气动力失稳与静力失稳的极限分析应置于同等重要的位置。

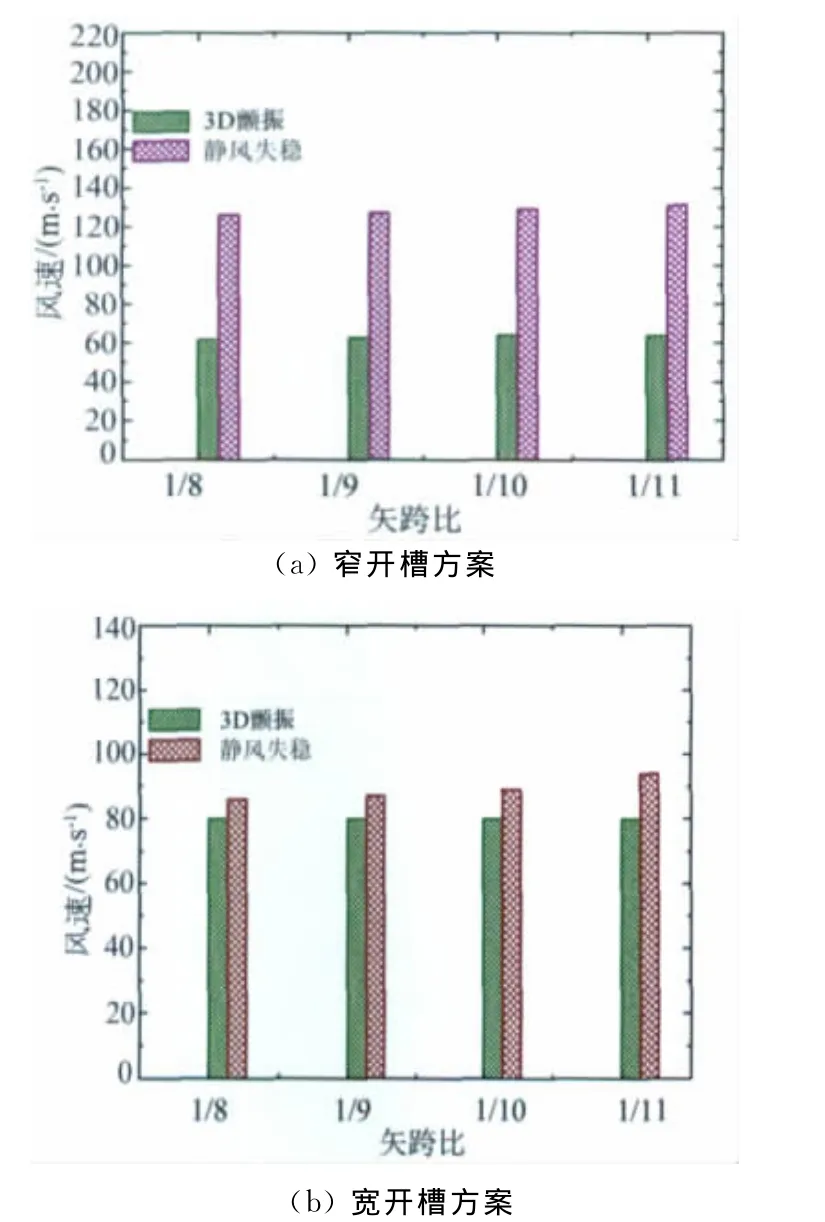
图4 颤振与静风失稳临界风速的对比Fig.4 Comparison of critical flutter wind speed with aero static stability critical wind speed

5 结 论

从三维颤振稳定性和三维三重非线性静风稳定性的角度，对5000m特大跨度悬索桥的空气动力稳定性能进行了仔细研究，得出如下结论：

（1）开槽加劲梁方案的最低颤振临界风速大于60m／s，最高达到74m／s；静风失稳临界风速大于120m／s，颤振发散先于静风失稳出现；颤振和静风失稳临界风速都随着矢跨比的减小有所升高；

（2）宽开槽加劲梁方案的最低颤振临界风速大于80m／s，最高达到89m／s，静风失稳临界风速最低为83m／s，最高为94m／s。颤振发散和静风失稳在相同的风速数量级出现，颤振失稳临界风速略大于静风失稳临界风速；颤振和静风失稳临界风速都随着矢跨比的减小有所升高；

（3）从颤振稳定性能的角度看，宽开槽加劲梁断面优于窄开槽加劲梁方案。但是从静风稳定性能的角度看，宽开槽加劲梁断面次于窄开槽加劲梁方案，综合考虑，宽开槽加劲梁方案在5000m特大跨度悬索桥的设计中优于窄开槽加劲梁断面；

（4）从三维空气动力稳定性能的角度证明：宽开槽和窄开槽加劲梁方案能给跨度达5000m的悬索桥提供足够高的颤振失稳与扭转发散临界风速，并能满足世界上绝大多数台风区的要求。

［1］ AGAR T.Aerodynamic flutter analysis of suspension bridges by a modal technique［J］.Engineering Structures，1989，11（2）：75－82.

［2］ BEITH J.A practical engineering method for the flutter analysis of long span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，77：357－366.

［3］ NAMINI A，ALBRECHT P，BOSCH H.Finite element－based flutter analysis of cable－suspended bridges［J］.Journal of Structural Engineering，1992，118（6）：1509－1526.

［4］ CHEN Z.The three dimensional analysis and behaviors investigation on the critical flutter state of bridges，1994.

［5］ JAIN A，JONES N，SCANLAN R.Coupled flutter and buffeting analysis of long－span bridges［J］.Journal of Structural Engineering，1996，122（7）：716－725.

［6］ MIYATA T，YAMADA H，KAZAMA K.On a application of the direct flutter FEM analysis for long－span bridges，1995.

［7］ MIYATA T，YAMADA H，KAZAMA K.Discussion on aeroelastic detail and control in the flutter occurrences of long－span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，1997，69：839－849.

［8］ DUNG N.Flutter responses in long span bridges with wind induced displacement by the mode tracing method［J］.Journal of Wind Engineering and Industrial Aerodynamics，1998，77：367－379.

［9］ XIANG H，GE Y.Refinements on aerodynamic stability analysis of super long－span bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12－15）：1493－1515.

［10］HUA X，CHEN Z.Full－order and multimode flutter analysis using ANSYS［J］.Finite Elements in Analysis and Design，2008，44（9－10）：537－551.

［11］DING Q，CHEN A，XIANG H.Coupled flutter analysis of long－span bridges by multimode and full－order approaches［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12－15）：1981－1993.

［12］ZHANG X，XIANG H，SUN B.Nonlinear aerostatic and aerodynamic analysis of long－span suspension bridges considering wind－structure interactions［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（9）：1065－1080.

［13］CHEN A，HE X，XIANG H.Identification of 18flutter derivatives of bridge decks［J］.Journal of Wind Engineering and Industrial Aerodynamics，2002，90（12－15）：2007－2022.

［14］CHEN X，MATSUMOTO M，KAREEM A.Aerodynamic coupling effects on flutter and buffeting of bridges［J］.Journal of Engineering Mechanics，2000，126：17.

［15］ZHANG X，SUN B，PENG W.Study on flutter characteristics of cable－supported bridges［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91（6）：841－854.

［16］MIYATA T，TADA K，SATO H，et al.New findings of coupled flutter in full model wind tunnel tests on the Akashi Kaikyo Bridge［C］.Proceeding of the Symposium on Cable－Stayed and Suspension Bridges，Deauville，France，1994：163－170.

［17］YASUI H，MARUKAWA H，GATAGIRI J，et al.Study of wind－induced response of long－span structure［J］.Journal of Wind Engineering and Industrial Aerodynamics，1999，83（1－3）：277－288.

［18］BOONYAPINYO V，LAUHATANON Y，LUKKUNAPRASIT P.Nonlinear aerostatic stability analysis of suspension bridges［J］.Engineering Structures，2006，28（5）：793－803.