基于支持向量机回归的电力系统负荷建模

崔晓祥，李娟

(1.江苏省电力公司检修分公司，江苏南京211102；2.上海施耐德电力技术有限公司，上海201200)

目前负荷建模方法大致可以分为两种：统计综合法和总体测辨法[1]。这些方法一般都是基于梯度的寻优，很容易陷入局部最优，不能有效地克服建模的非线性和连续性，因而得到的负荷模型与实际模型有较大的差别，在进行仿真时难以得出准确的结果。针对此问题，文中对支持向量机（SVM）在电力系统中负荷建模的应用进行了研究，通过实例表明采用SVM进行电力系统负荷建模，不但能描述负荷模型的非线性，且容易得到系统的全局最优解，且收敛速度也比较快。

1 SVM简介

SVM是由Vapnik在1979年最早提出的一种统计学习方法，以其良好的理论背景,从结构风险最小化原则为学习机器提供了一个崭新的角度。

简单地说，SVM的函数拟合就是用支持向量机对区域中的样本进行回归，由此确定该区域的映射函数，然后根据得到的拟合函数计算该区域中未知样本的取值。为逼近连续函数y=f（x），用函数集合：

式中：w为权系数；b为阈值；x为输入向量。定义损失函数如下：

约束条件：

式中：约束（w·w）≤C定义了结构风险；（xi，yi）为训练样本；m为训练样本数目。

ξ不敏感损失函数，定义为：

上面的问题等价于：

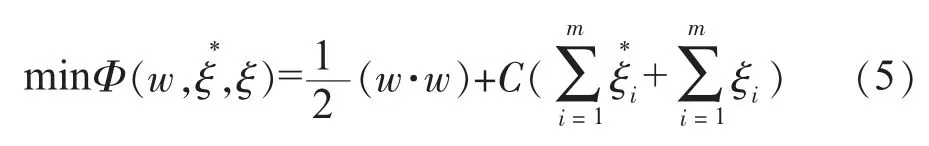
式中：常数C为误差惩罚因子，控制对超出误差的样本的惩罚程度。

2 运用SVM进行电力系统负荷建模

在电力系统负荷建模时，一般把电压和频率或者其偏差作为输入量，将有功和无功（或者有功电流和无功电流）或者其偏差量作为输出量。由于电网频率变化相对较小，因此，通常在建模时只考虑负荷功率随电压的变化特性。对于电力系统的有功和无功来说，它们是内在耦合的，但是为了建模的方便，可以将有功和无功进行解耦，分别对其进行建模[2]。

现在假定从一个给定的电力系统按照时间序列不间断地每隔一个周期采集一个点，该点包括电压、有功、无功数据，共采集l个：｛（u1，p1，q1），…，（ui，pi，qi），…，（ul，pl，ql）｝，其中ui，pi，qi分别为采集的电压、有功和无功值。将无功和有功分别进行建模，假设该系统是一个n阶系统，系统输入变量为｛（u1，p1），…，（ui，pi），…，（ul，pl）｝，｛（u1，q1），…，（ui，qi），…，（ul，ql）｝系统的输出变量为pk+1和qk+1，以这些输入输出数据为基础，采用一定的算法，找到能够满足NARMAX的函数依赖关系：

引入回归矢量：

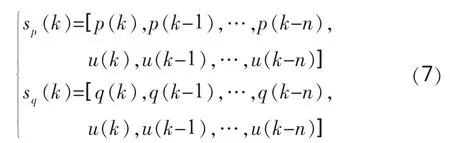
则式（6）可表达为：

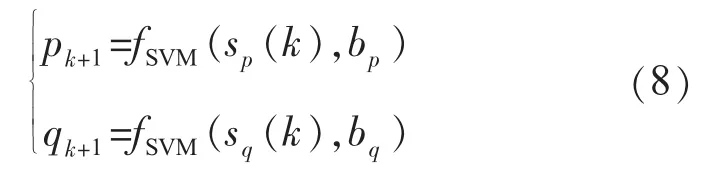
式中：bp和bq为阀值。建模的主要任务就是确定fSVM（）和fSVM（）以及bp和bq的具体值。

把电力系统负荷建模和自回归向量机的问题提法相比较可以发现，只要把回归矢量sp，sq和输出值pk+1，qk+1看作SVM的训练样本（p，u），（q，u），建模过程就是SVM的训练过程。因此电力系统的负荷建模完全可以用SVM的技术来解决。

3 SVM在线建模的步骤

运用SVM建立电力系统负荷模型的步骤：

（1）电力系统负荷群模型阶数的确定。对于非线性系统模型阶数,可以用很多种方法确定，文中采用损失函数法来确定（运用此方法得出后面的实例阶数为3阶）。

（2）选择SVM核类型及其核参数的确定[3]。

（3）SVM的训练。输入训练样本通过求解一个线性约束的二次规划问题,得到支持向量及其相应权值。对于输入维数很多的情况下，采用快速算法如SMO等特殊的算法,可以有效地解决回归函数逼近问题。

（4）模型校验。通过残差的自相关函数和一步预测误差判断模型的有效性，用不同的测试集进行交叉测试，如果误差均较小，则负荷模型可以接受。

4 实例仿真和计算结果的比较

文中对上海市电力公司所属的某变电站下的2号出线（该线路负荷较平稳，但是时有冲击负荷出现，因此比较适合检验负荷建模方法的精确性）所带负荷为建模对象，以1s为周期，不间断地采样300个点（包括电压、有功和无功）[4]，其中前200个点作为训练样本，后100个点作为模型效验。根据上述方法，得出该负荷群模型的阶数为3，因此采集的数据的SVM输入格式为：

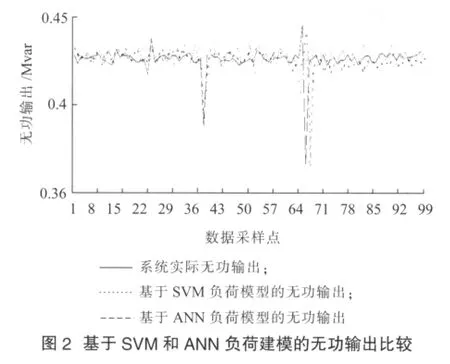
负荷建模的SVM输入空间为6维，输出空间为1维。利用软件包LIBSVM，选取的核函数为RBF，其中参数C选取为1000 。分别对系统的有功和无功负荷进行训练，经过训练，有功负荷建模得到197个支持向量，而无功负荷建模得到199个支持向量，应用这些SVM对负荷进行建模，并与实际系统的有功和无功输出（即后100点的有功、无功）相比较，得出其误差分别为0.0058 和0.0013[5]。

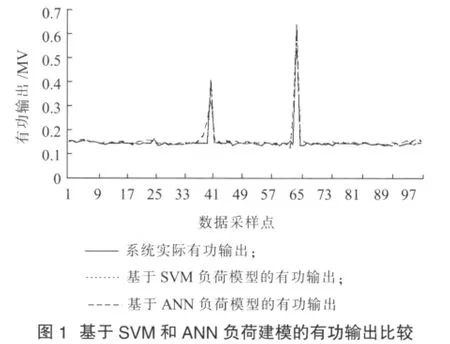
为了显示基于SVM回归的负荷建模的效果，运用ANN的BP算法对此系统进行有功和无功负荷建模[6]，得到有功和无功的误差分别为0.0504 和0.0151 。从误差的比较可以看出：相对于ANN的负荷建模精度，基于SVM负荷建模精度高出一个数量级。从图1和图2可以发现，在线路出现冲击负荷时，ANN的负荷建模相对于SVM有明显的误差，因此，基于SVM回归的负荷建模是一种非常有效的建模方法。

5 结束语

文中将SVM用于电力系统负荷建模，与ANN对同一线路的负荷群进行建模。结果表明，基于SVM回归的负荷建模的精度明显优于ANN的负荷建模。从而表明了应用SVM回归进行负荷建模是一种有效的建模方法，为负荷建模提供了新的途径。

[1] 牛东晓，曹树华，赵磊.电力负荷预测技术及其应用[M].北京：中国电力出版社，1998.

[2] 李元诚，方廷健，于尔铿.短期负荷预测的支持向量机方法研究[J].中国电机工程学报，2003，23(6)：55-59.

[3] 谢宏，魏江平，刘鹤立.短期负荷预测中支持向量机模型的参数选取和优化方法[J].中国电机工程学报，2006，26(22)：17-22.

[4] 姜惠兰，刘晓津，关颖，等.基于硬C均值聚类算法和支持向量机的电力系统短期负荷预测[J].电网技术，2006，30(8)：81-85.

[5] 牛东晓，贾建荣.改进GM（1，1）模型在电力负荷预测中的应用[J].电力科学与工程，2008，24（4）：28-30.

[6] 康重庆，夏青，沈瑜，等.电力系统负荷预测的综合模型[J].清华大学学报：自然科学版，1999，39（1）：8-11.