超临界压力下自然循环的静态特性

张项飞，匡 波，胡尚武，都立国

（1.上海交通大学核科学与工程学院，上海 200240；2.华东电力设计院，上海 200063）

第四代核能系统将采用的超临界水堆（SCWR），具有热效率高、经济性好等优点。在超临界压力下，水的物性在拟临界点将发生急剧变化，传热和流动过程非常复杂，特别这些过程与流道结构耦合对系统传热特性造成影响。超临界水堆采用非能动安全系统，如果系统发生静态或动态不稳定现象导致系统输热能力不足，可能导致设备损坏及安全系统的失效。因此研究水在超临界压力下自然循环的静态特性对于新一代核能系统的设计非常重要。本文针对超临界压力下典型自然循环回路模型，采用基于延拓的非线性数值方法求解，并分析其静态特性，同时讨论一些回路参数对运行效果的影响。

1 数学模型

典型的自然循环由下降段、下水平段、加热段、上升段、上水平段、冷却段和压力控制器组成，压力控制器为恒压，见图1。

为了便于讨论，本文假设：水的自然循环为一维稳态流动；忽略流动回路中因摩擦等损耗形成的热效应，并忽略流体轴向导热；同时假定回路中的冷却段冷却功率等于加热功率。自然循环的模型由控制方程组成。

质量方程：

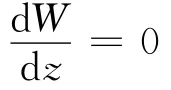
动量方程：

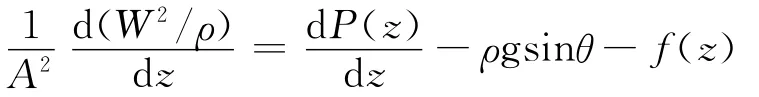
图1 自然循环回路示意图

能量方程：

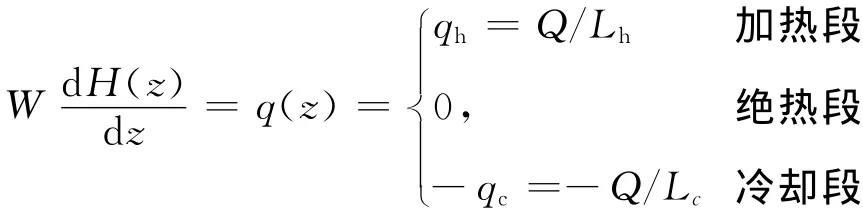
式中：W为回路平衡质量流量；z为沿回路流向上的坐标；ρ为流体密度；g为重力加速度；f（z）为回路截面（z）处的阻力压降梯度（包括沿程摩擦ffr和局部阻力fl）；θ为某点出发水平向右方向与该点流动方向之间的逆时针夹角；H（z）为截面z处水的焓值；q（z）为截面z处的加热或冷却线功率；qh、qc分别为加热段和冷却段线功率值；Lh、Lc分别为加热段和冷却段长度。

对动量方程沿回路积分：

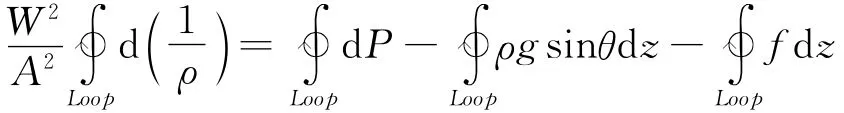
由于：

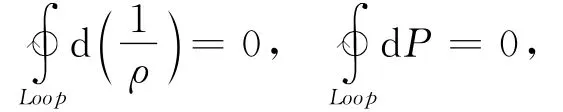
可以得到：

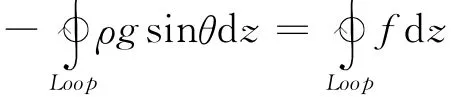
等式的左边为驱动力，右边是阻力，二者相等时回路达到平衡，于是求解整个回路平衡解即是求解驱动力阻力平衡方程：

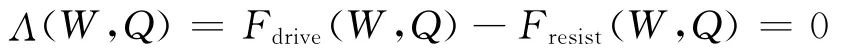
通过对整个回路进行节点划分，可以根据模型对水力学方程进行离散化求解，离散方程为：

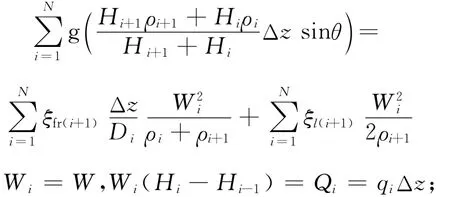
式中：ξfr为沿程阻力系数；ξl为局部阻力系数。

本文采用Kondrat’ev关联式计算绝热段沿程阻力，使用Filonenko关联式计算非绝热段沿程阻力。阻力系数：

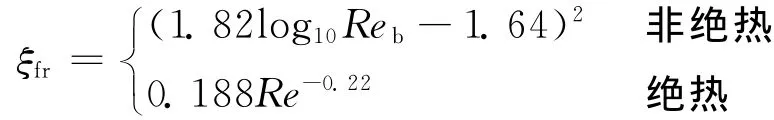
本文采用基于延拓的非线性数值方法求解Λ（W，Q）＝0，得到一组功率流量值，即是平衡方程的解图。数值模型回路的几何尺寸及节点划分如表1所示。

表1 回路管道尺寸及节点划分

2 静态特性计算结果

基于所建的自然循环回路，系统压力为25 MPa，选取加热段入口温度分别为480 K和380 K，加热段功率为0～1100 k W（均匀加热）。通过数值求解，得到该自然循环回路两组典型的功率－流量曲线，如图2所示。

图2 加热功率与流量的典型关系

可以看到，回路中的平衡流量W 首先随着加热功率Q的增加而较快地增加到最大值Wm，然后随着加热功率继续增大，流量急剧下降，进入传热不利区域。此时Wm为此热力条件下回路的最大自然循环流量，反映了回路的最大自然循环能力。显然，这（Qm，Wm）以后的区域对实际设备传热与系统输热应用是十分不利的，工程上（如SCWR非能动余热排出系统）应避免系统回路启动过程中途径此区域或在此不利区域（流量突降区）运行。最大流量值对应的功率值Qm反映了该自然循环系统的最大输热能力。

进一步计算表明，当加热功率Q升到加热段出口处的水正好处于拟临界点附近区域（大比热区）时，循环回路的流量达到其最大值Wm。以加热段入口温度Tin为480 K时的循环工况为例，图3给出了相应水动力特性曲线（流量－加热功率曲线）上（W1，Q1）、（W2，Q2）、（W3，Q3）三个静态流量工作点工况下，加热段各处主流温度及相应的比热分布，分别对应于加热功率为400 k W、649 k W和820 k W，对应的温度分布曲线分别是t1、 t2、t3；比热容分布曲线分别为cp1、cp2、cp3。可以看到，对应于最大自然循环能力Wm及最大输热能力限Qm的工况下，加热段内超临界水的比热容峰值（拟临界点）正好位于加热段出口附近处。

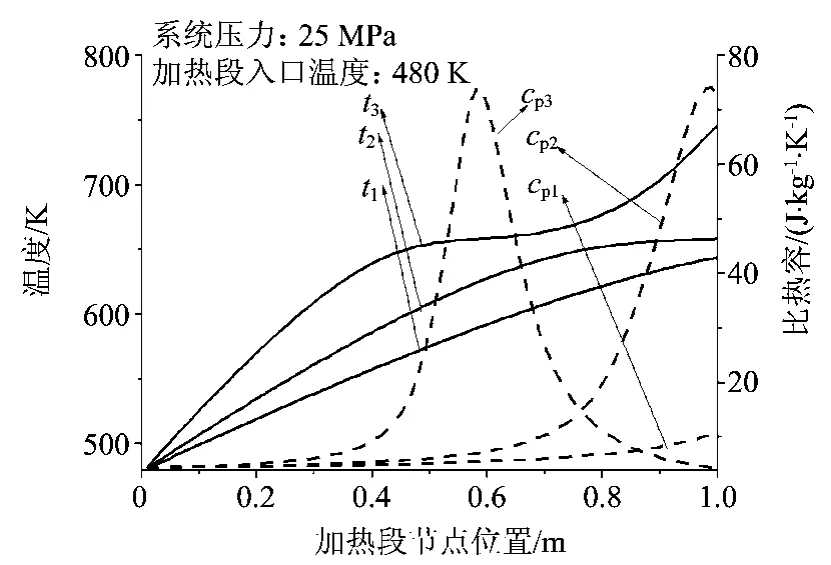
图3 加热段节点温度及比热分布

3 静态流动的稳定性分析

对图2中入口温度为380 K功率－流量曲线的静态流动不稳定区域局部放大，如图4所示。

图4 加热段入口温度为380 K时功率－流量曲线

可以看出，在（Qm，Wm）之后的附近区域静态流动出现了不稳定现象（流量漂移），亦即存在某一加热功率对应于3个循环流量值现象，水动力方程在此区域出现多解。当系统运行于Q1、Q2之间的某一加热功率时，可能由于微小流量扰动而发生流量的突然跌落或陡升现象。应该指出，对于超临界压力下的自然循环回路，这一流量漂移现象主要发生在入口温度较低的情况，不稳定区域范围也比较小。针对入口温度为380 K的情况下，不同加热功率对应的解进行分析如下。

（1）Q＜Q2和Q＞Q1，分别对应于图5和图6驱动力阻力曲线。可以看到，两图曲线都有一个交点，在交点附近，如流量变化很小的＋ΔW 时，阻力大于驱动力，驱动力与阻力相互作用使其流量减小回到该点；当流量变化很小的－ΔW 时，驱动力大于阻力，促使流量增加，又回到该点。因此这个唯一的平衡点是稳定的，不会发生流动不稳定。

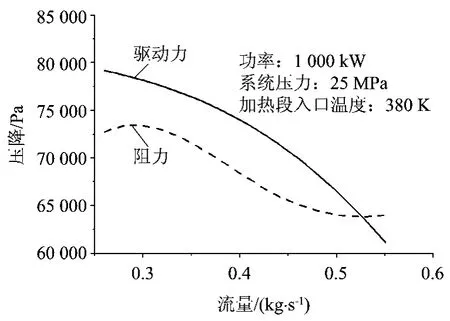
图5 回路驱动力与阻力关系（Q＜Q2）

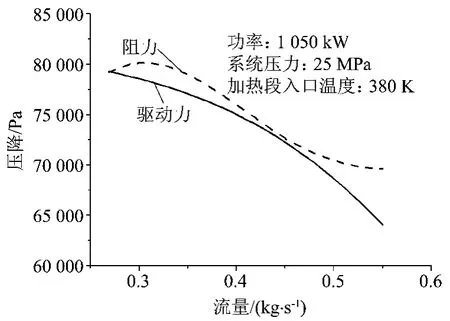
图6 回路驱动力与阻力曲线关系（Q＞Q1）

（2）Q2＜Q＜Q1的运行区域，存在三个平衡质量流量，对应于图7驱动力阻力曲线。对该图中左侧和右侧的交点类似于图5和图6中的交点，是稳定的。但对于中间平衡解，如果流量变化＋ΔW 很小时，驱动力大于阻力，使流量继续增加，直至增加到右侧的稳定点；如流量变化－ΔW很小时，阻力大于驱动力，将使流量继续减小，直至减小到，左侧的稳定点。因此中间交点不稳定，会引起流量漂移。

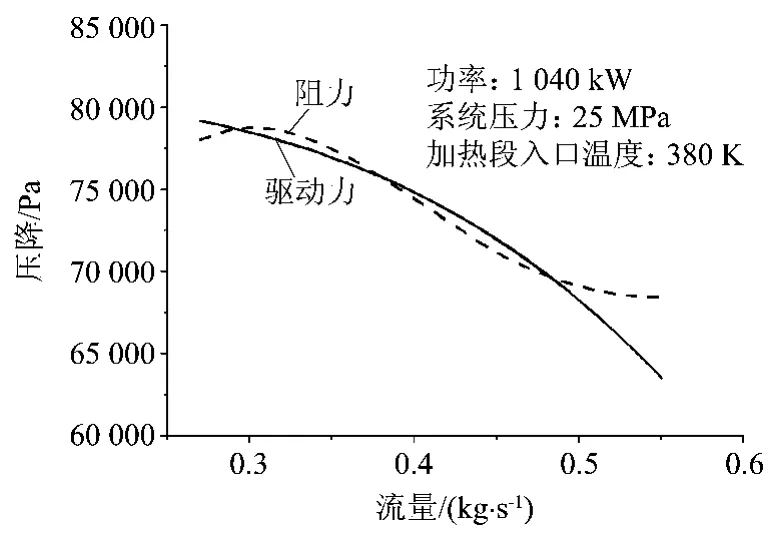
图7 回路驱动力与阻力曲线关系

（3）Q＝Q1和Q＝Q2，分别如图8和图9所示，驱动力阻力曲线对应有一个交点和一个切点。其中在交点处系统是稳定的，但在切点处，很小的扰动流量就会发生偏移，切点为转变点。

图8 回路驱动力与阻力关系（Q＝Q1）

图9 回路驱动力与阻力关系（Q＝Q2）

针对本文讨论的工况，不同的入口温度分别得到对应的流动不稳定功率范围如图10所示。可以看到，对于特定回路，在某一压力下，加热段入口温度越低，出现静态不稳定的区域也越大，因此，当入口温度达到一定值后，就不会再出现静态不稳定性。实际应用中可以通过提高加热段入口温度的方式，来减小流动不稳定区域甚至消除流动不稳定性现象。

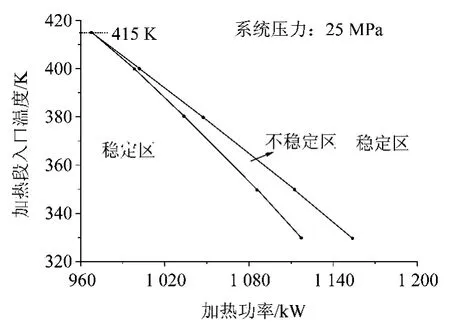
图10 回路不同压力下的稳定区域

4 参数效应

4.1 系统压力的影响

图11和图12分别为入口温度为480 K和380 K在压力23 MPa、25 MPa和27 MPa下的功率流量曲线。

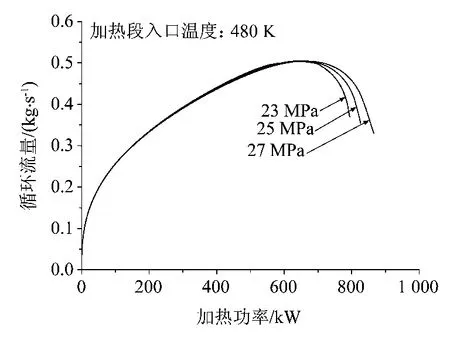
图11 入口温度480 K不同压力下功率流量

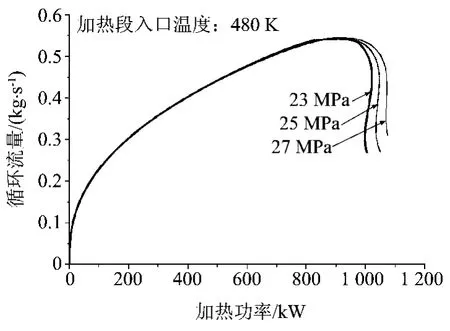
图12 入口温度380 K不同压力下功率流量

可以看到：系统压力的增大，对自然循环回路最大自然循环能力Wm以及系统在输传热不利区以前的水动力特性影响极小，随着系统压力的升高，回路的加热功率－循环流量曲线在Q＞Qm的区域趋于平缓，有利于自然循环回路的输传热以及设备安全。

由图12可以注意到，随着系统压力的升高，位于Q＞Qm输传热不利区的静态不稳定性区域范围也有所减小，静态不稳定区域随着压力升高略微右移，也就是说较高压下需要更大的加热功率方能进入不稳定区。总之，随着系统压力升高，流量漂移现象更不容易发生了。

图13给出了本文计算的典型自然循环回路在不同系统压力下（p＝23、25、27 MPa）的静态流动不稳定性的稳定域。可以看到：随着系统压力的升高，回路出现静态不稳定性的范围越来越小，而且发生静态不稳定性的上限温度也大大降低。

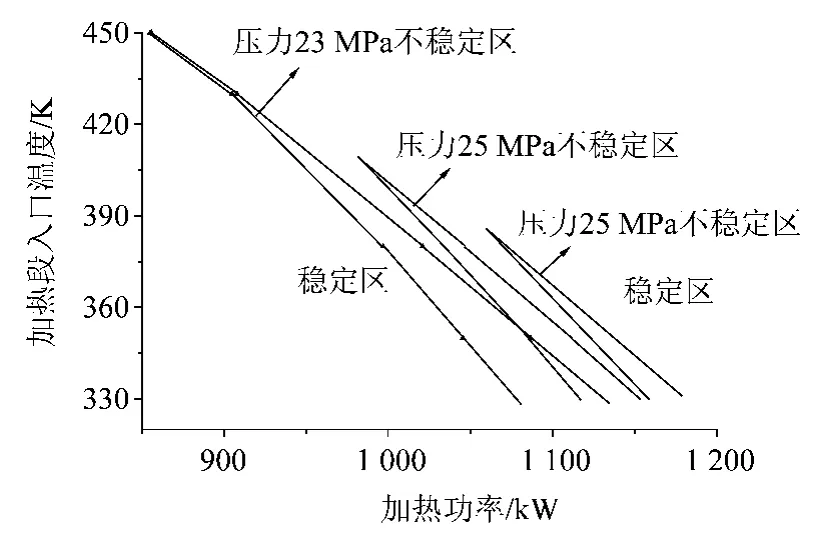
图13 回路不同压力下的稳定区域

4.2 管径的影响

为了探讨管径对超临界压力下自然循环水动力特性的影响，本文计算了若干回路管径条件下（Dheating＝18、21、24 mm）典型自然循环回路的加热功率－循环流量特性。在加热段入口温度480 K和380 K时，不同管径下的加热功率－循环流量曲线分别如图14和图15所示。

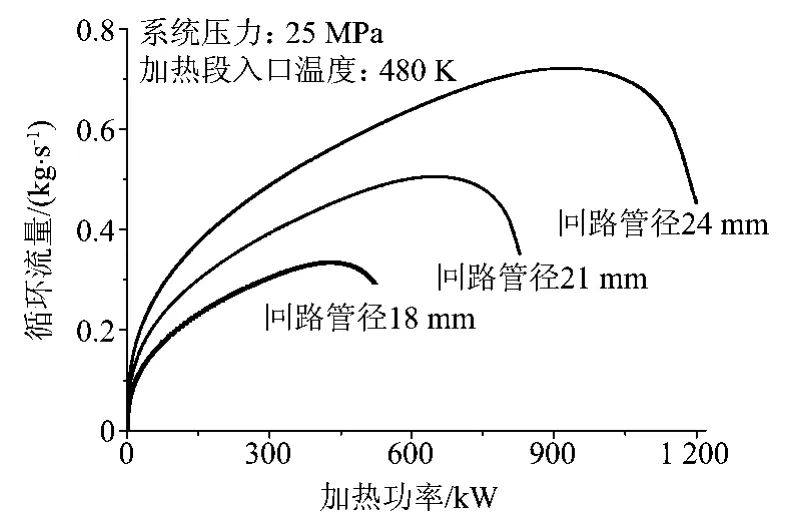
图14 入口温度480 K不同管径下功率流量曲线

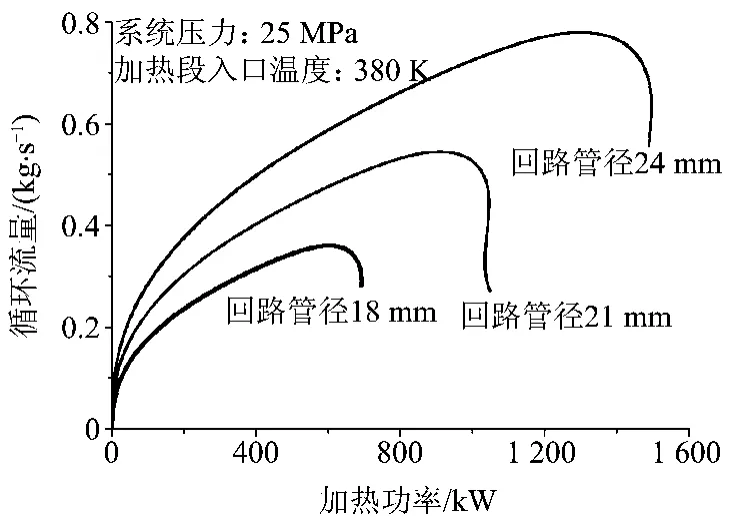
图15 入口温度380 K不同管径下功率流量曲线

由图14和图15可见，回路管径增大，回路的自然循环能力及输热能力限（Wm和Qm）均大幅增加，这对回路系统的输传热是有利的。

同时在图16中可看到，随着管径的加大，静态不稳定性区域与发生流动静态不稳定的上限温度变化并不显著，但是相应发生静态不稳定所需要的加热功率明显增加。

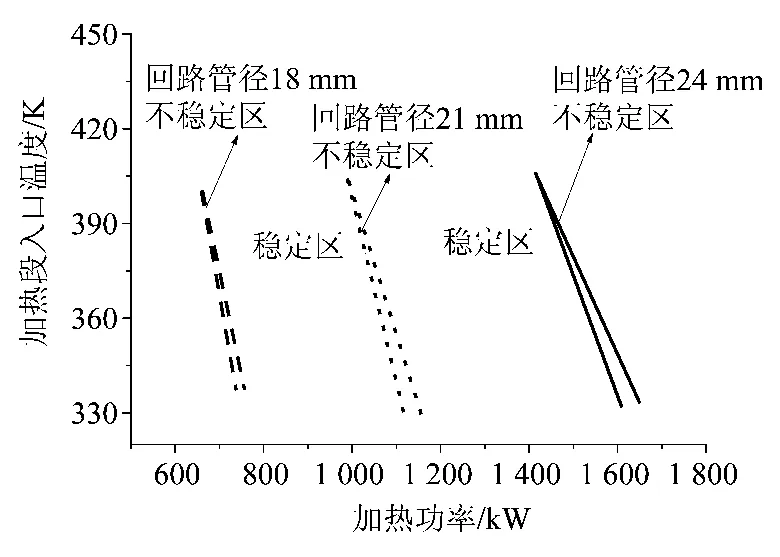
图16 回路不同直径对应的稳定区域

4.3 冷热高度差的影响

回路高度（常以冷、热位心高度差表示）在自然循环中是一个重要的影响因素，在亚临界单相与两相自然循环系统中，自然循环高度对自然循环能力的影响是不同的，两相自然循环流量一般来说要远大于单相自然循环。图17和图18分别给出了加热段入口温度480 K和380 K条件下，不同冷热心差对自然循环水动力特性的影响。

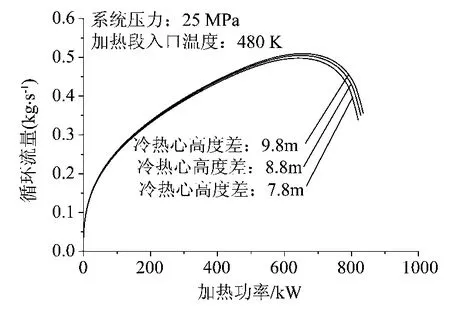
图17 入口温度480 K不同回路高度下功率流量曲线

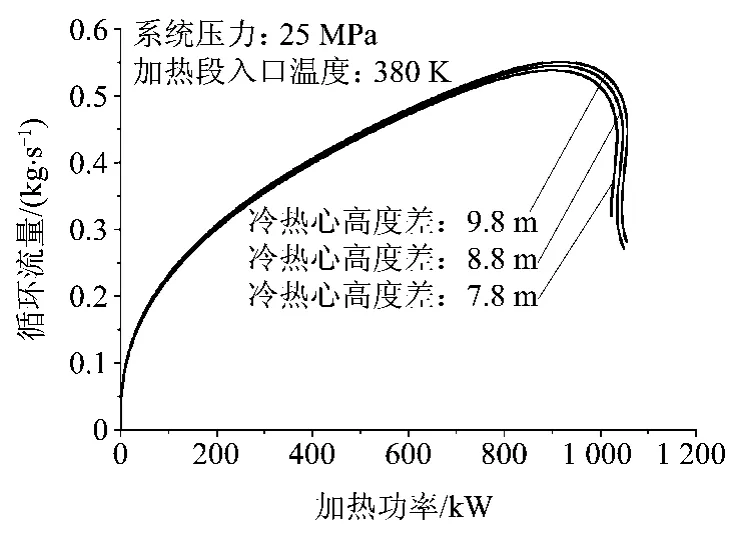
图18 入口温度380 K不同回路高度下功率流量曲线

可以看到：超临界压力下自然循环回路的冷热心高度差对回路最大自然循环能力Wm以及最大输热能力限Qm都略有影响；随着高度差增大，自然循环能力及回路输热能力限是有所提高的，但提高的幅度有限；相应地，加热功率一定的情况下，加热段出口温度也有所降低。冷热心高度差的影响幅度主要是由回路的浮升驱动力与流动阻力特性共同决定的。

同时还注意到，冷热心高度差对回路流动静态不稳定性特性也会有所影响（见图18），同样地，影响不显著。计算结果表明：自然循环回路的冷热心高度差对回路的静态稳定域有影响，高度差增加使得不稳定区域略微右移，但对位置的影响不大，高差对回路发生流量漂移的加热段入口上限温度影响甚微，见图19。

图19 回路冷热高度差对应的稳定区域

4.4 加热段入口局部阻力的影响

局部阻力是自然循环总阻力的一部分，特别是加热段入口与出口的局部阻力对回路自然循环能力及其输热有较重要的影响。本文就加热段入口温度480 K和380 K两种情况，分别对加热段入口局部阻力系数设置为0、5、10，计算比较加热段入口局部阻力对超临界压力下自然循环回路水动力特性的影响。计算结果如图20和图21所示。

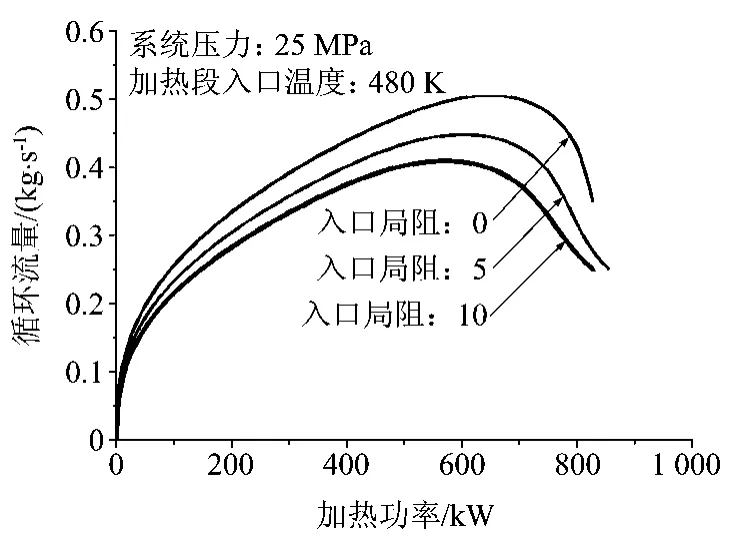
图20 入口温度480 K不同局部阻力下功率流量

计算分析表明：增大加热段出口和入口的局阻，都会降低回路的最大自然循环能力Wm及最大输热能力限Qm；但是，一旦加热量超过了Qm，燃料将进入输传热不利区域，增加入口局阻，循环流量降低会稍缓一些，而且将减小发生流动静态不稳定性范围，甚至避免发生静态不稳定，而增加出口局阻则不会出现这样的效应。

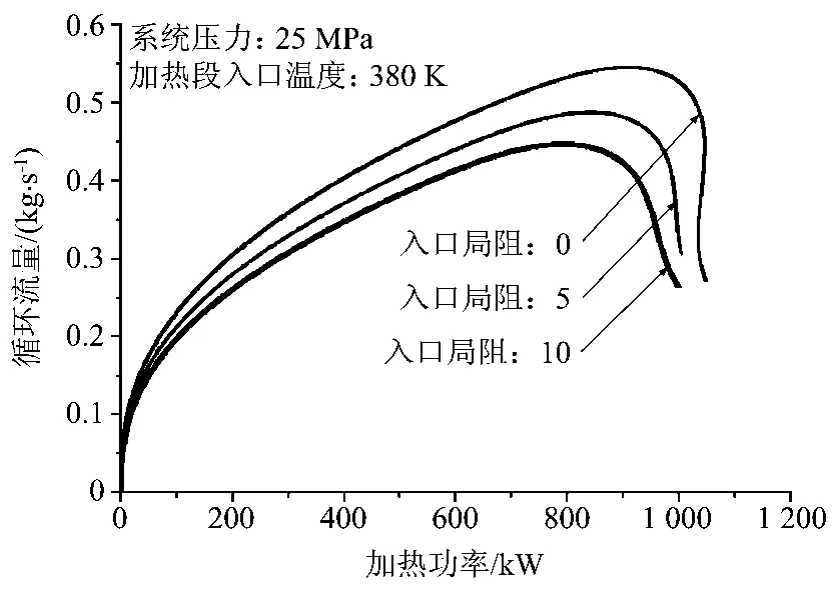
图21 入口温度380 K局部阻力下功率流量

5 结语

（1）本文建立了超临界压力下自然循环回路模型，对其进行数值分析并计算得到静态功率流量特性曲线。发现在较低的入口温度下，出现了静态流动不稳定性现象，并得到了基于加热段入口温度的不稳定区域。

（2）讨论了不同参数因素对静态流动特性及稳定域的影响，其中管径大小、系统压力大小及入口局部阻力大小对系统自然循环能力及最大输热能力限值影响较大，而回路冷热高度差及系统压力较之影响微弱。其中增大系统压力及加热段入口局部阻力，会减小流动不稳定区域，利于系统输热。

［1］ Jiyang Yu，Shuwei Che，Ran Li，Bingxue Qi.Analysis of Ledineggow instability in natural circulation at supercritical pressure［J］.Progress in Nuclear Energy，2011（53）：775-779

［2］ Kuang Bo，Du Li-Guo.A Comparative study on hydraulic features of supercritical water naturaland forced circulation loops［C］，The 2ndCanada-China Joint Workshop on Supercritical Water-Cooled Reactors（CCSC-2010）

［3］ Igor L Pioro，Romney B Duffey，Tyler J Dumouchel.Hydraulic resistance of fluids flowing in channels at supercritical pressures（survey）［J］.Nuclear Engineering and Design，2004，231：187-197.

［4］ M.Kubicek，M.Marek，Computational Methods inBifurcation Theory and Dissipative structures［M］.Spring-Verlag New York Inc.：Newyork，1983：43-48