基于均值平移和自适应预测的运动目标跟踪＊

余 朗 王杜娟 乐竹雄

（武汉理工大学理学院 武汉 430070） （武汉理工大学信息工程学院 武汉 430070）

0 引 言

运动目标跟踪是计算机视觉研究的核心技术，而目标跟踪中存在的困难很大程度上是实际环境中目标运动的复杂性以及视频数据具有的特殊性、复杂性造成的，比如目标旋转、大小变形、运动速度、目标颜色与背景颜色的相似程度、背景混乱及遮挡等.

视频序列的目标跟踪算法必须满足实时性、鲁棒性两个要求.目前算法大体分为4类：（1）基于运动检测的跟踪［1］.背景差分算法、帧间差分算法、光流法检测等，通过检测运动目标对应区域的变化进行跟踪；（2）基于目标特征的匹配跟踪.特征可以是二值化分割图像［2］、目标颜色直方图［3］、边缘特征点、角点等，利用特征对复杂场景下的目标进行跟踪，实时性比较高；（3）基于活动轮廓的跟踪：主动轮廓线跟踪 （snake）、基于 Huasdoff距离的轮廓跟踪在军事、视频监视等场合得到广泛的应用；（4）基于模型的跟踪［4］.线图模型、二维轮廓和三维立体模型，在目标形态变化和部分遮挡情况下也能精确分析目标的运动轨迹.

Mean Shift算法［5］采用核概率密度来描述目标的特征，然后利用均值平移搜寻目标位置.抗干扰能力强，对目标旋转和部分遮挡不敏感，计算速度快.但跟踪过程中没有涉及模板更新、易受光照变化影响、提取目标特征单一无法适应严重遮挡等.粒子滤波具有很好的鲁棒性，跟踪精度高，抗干扰能力强，但运算量大，很难应用到实时跟踪系统中.文献［6］引入Kalman滤波解决了初始点的选择问题.

一个鲁棒的跟踪算法应该能准确的判定遮挡发生，并且在遮挡期间利用目标剩余的信息继续跟踪目标，即使在目标被完全遮挡情况下也不至于丢失目标.克服遮挡问题，关键看遮挡结束后正确的跟踪是否能得到恢复.

1 基于Mean Shift的跟踪算法简介

1.1 目标模型与候选模型

初始帧中选定一个包含跟踪目标的矩形窗口，窗口内共有n个像素点.将窗口内像素点的颜色量化成Rm×Gm×Bm级，构成一个颜色特征空间，特征值个数为m.对目标区域内所有像素点，计算特征空间中每个特征值的概率称为目标模型的描述.第u个特征值的概率为

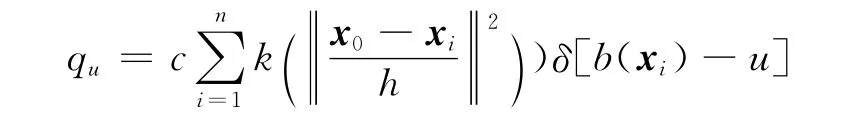
式中：x0为窗口的中心像素坐标；xi为第i个像素的坐标；k（x）为核函数K（x）的轮廓函数；h为核窗宽；b和δ为判断xi处的颜色值是否属于特征值u；c为归一化常数；h为等于目标区域外接圆的半径大小.

候选目标中特征值u的概率为pu（y0），y0是当前帧中候选目标区域中心，跟踪的任务就是要找出y0.

1.2 相似性度量函数

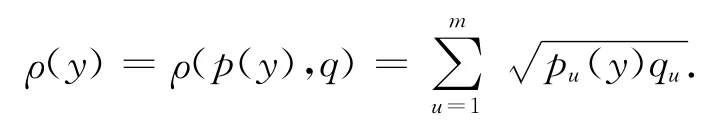
2 基于改进的均值平移算法的目标跟踪

基于Mean Shift算法采用跟踪目标的颜色分布作为特征，用Bhattacharyya系数来衡量目标模型和候选目标区域对应的直方图之间的相似性.当Bhattacharyya系数小于一定值时，采用粒子滤波器进行预测，目标被完全遮挡时，Bhattacharyya系数达到较低值，此时只进行运动预测，并继续用粒子滤波器寻找目标，这样目标一出现就可以马上被捕捉到；当目标恢复正常运动时，Bhattacharyya系数逐渐增大，大于一定值时，转为Kalman预测.

2.1 Kalman滤波器 的引入

设目标中心在x，y轴上均是一个被随机加速扰动的直线运动，加速度a（t）～N），

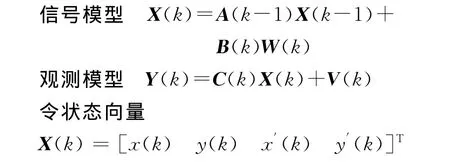
分量表示目标中心在x，y轴上的位置和速度；观测向量Y（k）＝［xc（k） yc（k）］T，表示当前帧中观测到的目标中心在x，y轴上坐标量；设W（k），V（k）为零均值正态白噪声序列.

当前帧中，预测估计值X（k）的目标分量与观测值Y（k）之差记为滤波器残差

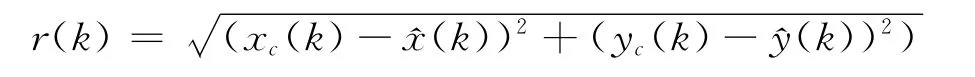
经过若干帧后，Kalman滤波器稳定运行，则r（k）较小.由于当前帧中目标区域内融入很多的非目标信息，Mean shift以滤波器提供的起始点开始，寻找最佳目标，可能得到的位置会远离起始点，使得滤波残差会远大于平时的r（k），这时可判断目标可能遇到大的遮挡.设定阈值Tdist判断目标是否发生遮挡.

2.2 模板更新策略

模板更新遵循原则：目标缓慢改变时模型随之缓慢改变，目标剧烈变化时不更改模型.

若当前帧中的Kalman残差满足 r（k）＜Tdist

模板更新条件 ρ（pu（y），qu）≥Tud

更新方程

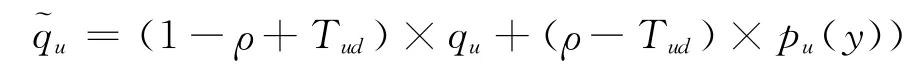
式中：Tud为更新阈值；qu为先前目标模板；pu（y）为在当前帧中跟踪到的目标特征分布；为更新后的目标模板.

考虑到目标遮挡和跟踪偏离都会导致Bhattacharyya系数减小，当跟踪偏离目标时而导致相似性系数减小，更新模板则会导致跟踪失败.所以在检测到当Bhattacharyya系数小于一定值时，先结合粒子预测进行一次跟踪，若系数值仍小于给定值，则进行目标模板更新.

2.3 粒子滤波理论在目标跟踪中的应用

遮挡情况下改进的粒子滤波算法.研究发现，在非遮挡情况下，根据预测的准确程度自适应选择粒子数量以保证跟踪的实时性，并自适应的选择运动模型中高斯噪声的方差以保证粒子的有效性；而在遮挡情况下和不规则运动时，运动模型中的确定性预测部分不再可靠［7］.所以要改变目标的运动模型，粒子只做布朗运动，并且各粒子经过均值平移算法的一步迭代进行优化，不仅保证实时性，防止发生“过优化”，更能使遮挡后的跟踪更快恢复.

1）系统动态模型的建立 选用二阶自回归过程（ARP）方程

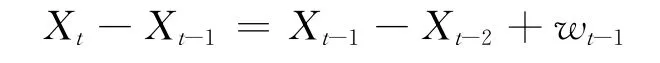
式中：Xt为t时刻的目标状态；wt－1～N（0，σ2）.上式等号右侧的前两项为运动位移量确定性预测；wt－1项即布朗运动，其方差决定了粒子布朗运动的范围.

由于遮挡情况下跟踪不稳定，运动模型中的确定性预测不再可靠，所以只利用高斯噪声部分，粒子只做布朗运动，选用一阶ARP方程 Xt－Xt－1＝wt－1.

3）系统观测模型的建立 利用当前帧目标的特征和初始帧目标的特征之间的相似度表示观测值.通过对每个粒子计算当前帧中的候选模型来计算Bhattacharyya相似度，然后利用加权后的相似度计算相似距离di＝得观测值的概率密度函数

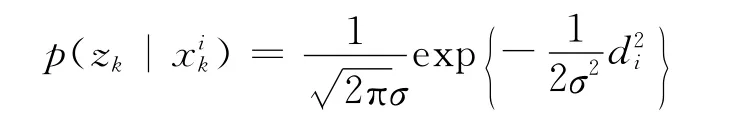
4）目标位置的确定

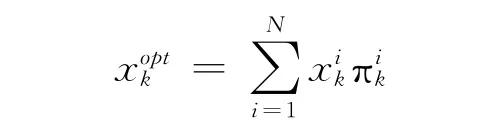
5）重采样 通过对后验概率密度再采样Ns次，产生新的粒子集：，淘汰权重小的粒子而保留或复制权重大的粒子，用新的粒子集近似p（xk｜z1：k）的离散分布，使得原来带权重的粒子集映射为等权重粒子集.这些新粒子进入下一帧的计算中，系统动态模型改变粒子位置，观测模型改变粒子的权值，确定目标的位置，重采样不断循环进行.

6）基于均值平移的粒子优化 重采样之后，抛弃了权值小的粒子，保留权值大的粒子，由权值大的粒子衍生出新的权值相同的粒子.然后利用均值平移理论对每个新产生的粒子进行迭代之后，新粒子会自动集中在目标邻近的局部最大值区域内，而同一局部最大值区域也会集中较多的粒子，因此用较少的粒子就可以实现目标跟踪.

2.4 跟踪算法步骤

步骤4 计算新的平移位置

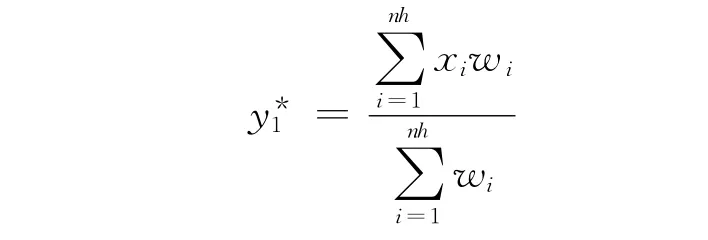
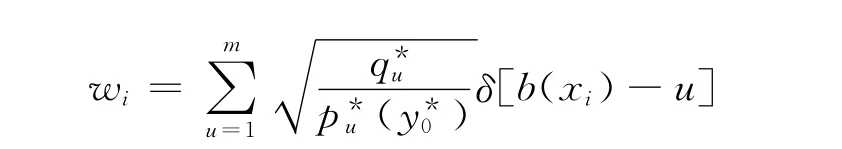
步骤6 计算Bhattacharyya系数ρt.

步骤7 若ρt＜th1，令t＝t＋1，转步骤1；若ρt＜th2，则遮挡情况下判为目标完全遮挡，只用粒子滤波器捕捉目标，不进行目标模型更新，否则，判为模型平移，重新获取模型.若连续n帧ρt＜th2，则判为目标消失，停止跟踪.若th2＜ρt＜th1，则进一步判断.

若ρt－2＞ρt－1且ρt－1＞ρt（目标进入遮挡），或者ρt－2＜ρt－1且ρt－1＜ρt（目标离开遮挡），转下一步，否则结合粒子滤波进行一步跟踪；若仍满足该条件，则按方程更新目标模型，令t＝t＋1，转步骤1.

步骤8 令t＝t＋1，运用Xt－Xt－1＝wt－1采样N个粒子集，计算加权相似系数完成目标在当前帧的状态估计，令y＊0＝（x，y），转步骤2.

3 实验结果分析

本文提出的改进算法在MATLAB 6.0环境下对两个不同视频序列分别进行跟踪测试.图1为静态遮挡行人视频序列共87帧，给出部分跟踪结果5帧（从左往右帧序号依次为37，46，60，67），设置ε＝1，Tud＝0.683，th1＝0.985，th2＝0.973.跟踪目标选为行人的头部，目标从左往右的移动过程中，存在着一个被遮挡的程度由小变大，再由大变小这样一个过程，依靠改进算法的鲁棒性，在目标严重遮挡后又很快重新锁定了目标.图2为http：／／homepages.inf.ed.ac.uk／rbf／CAVIAR 提供的动态目标遮挡视频序列共260帧（从左往右帧序号依次为191，221，234，257），参数设置同上.跟踪目标既存在不规则运动又存在严重遮挡和完全遮挡.运用本文算法，通过观测Bhattacharyya系数值切换滤波器保证目标的有效跟踪，完全遮挡消失后很快捕捉目标，目标恢复正常运动时，又切换到卡尔曼预测，保证了实时性和鲁棒性.

4 结束语

图1 静态遮挡行人视频序列

图2 动态目标遮挡视频序列

本文提出结合均值平移和自适应预测的目标跟踪算法，引入Kalman滤波器为Mean Shift算法估计初始点，在跟踪稳定情况下进行模板更新，根据Kalman残差大小判定是否发生遮挡：部分遮挡情况下结合Kalman滤波实现对快速运动目标的实时跟踪；完全遮挡情况下结合粒子滤波进行鲁棒跟踪.实验证明，改进的算法可以有效地提高跟踪算法的效率，特别是能很好地解决遮挡问题.

［1］MCKENNA S，ROSENELD S J，WESHSLER H.Tracking groups of people［J］.Computer Vision and Image Understanding，2000，80（1）：42－56.

［2］CHANG Fangling，MA Li，QIAO Yizheng.Target tracking under occlusion by combining interral intensity matching with multi－block－voting［J］.Lecture Notesin Computer Science，2005，3644（1）：77－86.

［3］QIAO Jorgehong，WAN Anhua，LIU Yu.Persontracking with occlusion using appearance filters［J］.IEEE／RJ International Conference On Intelligent Robost and systems Oct.，2006.

［4］朱胜利.快速运动目标的Mean Shift跟踪算法［J］.光电工程2006，33（5）：66－70.

［5］DIRIK C，JACOB B.The performance of PC solidstatedisks as a function of band width，concurrency，architecture，organization［C］／／Proce－edings of the 36th annual international symposium on Computer architecture.Austin，2009：279－289.

［6］JIA Jingping，WANG Qing.Object tracking by mulit－degrees of freedom mean shift procedusr combined with the Kalman particle filter algorithm［C］／／Proceedings of the 15th International Conf.on Machine Learning and Dalian，13－16August 2006.

［7］强世锦，荣 健，滑 玉.基于粒子预测的非线性状态目标跟踪算法［J］.武汉理工大学学报：交通科学与工程版，2008，30（2）：113－115.