Julia集和Mandelbrot集的反演变换

李劲菲， 盛中平

（1. 大庆石油高级中学，黑龙江 大庆 163712；2. 东北师范大学数学与统计学院，吉林 长春 130024）

Julia集和Mandelbrot集的反演变换

李劲菲1， 盛中平2

（1. 大庆石油高级中学，黑龙江 大庆 163712；2. 东北师范大学数学与统计学院，吉林 长春 130024）

论文讨论了居里叶集与曼德尔布罗特集的反演变换问题，通过扩充复平面上关于任意定点的反演变换，获得了两类共轭函数。使得这两类共轭函数的居里叶集与曼德尔布罗特集，恰好是原居里叶集与曼德尔布罗特集关于定点的反演变换,并运用逃逸时间算法绘制居里叶集和曼德尔布罗特集的反演图。

分形；反演图；逃逸时间算法；Julia集；Mandelbrot集

近年来，Mandelbrot集和Julia集以其美丽和复杂引起了各国科学家的关注和研究，并且利用计算机图形学绘制Mandelbrot集和Julia集。文献[1]用VB语言实现Mandelbrot集分形图的编程过程和结果，实现了用拖拽鼠标进行Mandelbrot集分形图的局部放大显示的功能。文献[2]对传统的Mandelbrot集计算机生成算法提出改进方案，增加了算法内循环中的测试功能，在复平面上对算法内循环中的点进行重复计算，更加准确、艺术地描述出了Mandelbrot集的内部结构。文献[3]构造了一系列复映射 z→ zα+ c( α ∈ R)的广义Mandelbrot-Julia集的内部结构图。文献[4-5]深入研究了Mandelbrot集和Julia集的关系，在四维空间中建立了Mandelbrot集和Julia集的统一模型，并且得出了Mandelbrot集的芽体的周期的特点。文献[6-7]提出了一个解决非解析复迭代的Mandelbrot集和Julia集的研究方法，并用此方法得出了一些结论。本文将基于文献[8]的一些结果做进一步的推广。

1 Julia集和Mandelbrot集

Mandelbrot集和 Julia集是分形领域中典型的例子，绘制它们的算法是逃逸时间算法。文献[8]给出了生成的Julia集和的Mandelbrot集的图像，本文将推广此结果，给出其一般形式。

下面，先给出Julia集的定义。

定义 1 一般由一个二次复映射 f(z)= z2+ c, 对某一个确定的参数c∈C，复平面上的点z，从某一初始值 z0出发，进行反复迭代运算z = z2+ c(n = 0,1,2 …)，那么所有使迭代n+1n函数 f( z)不发散的起始点的集合就构成了一个填充的Julia集。而真正的Julia集则是指填充Julia集的边界。

最后，给出Mandelbrot集的定义。

定义3 由一个二次复映射 f( z )=z2+c，对于复平面上的任意点c，进行反复迭代运算 zn+1=那么使所得序列有界c值的集合就构成了Mandelbrot集fM 。

定义 4 由一个二次复映射 f(z )= z2+对于复平面上的任意点c，进行反复迭代运算n= 0,1,2 …)，那么使所得序列有界的 c值集合就构成了Mandelbrot集 Mf。

以上定义是利用逃逸时间算法生成 Julia集和Mandelbrot集的基础。下面将利用逃逸时间算法做出Julia集和Mandelbrot集，通过图形对比得出两个重要的定理。

2 试验与结果

2.1 逃逸时间算法基本思想

逃逸时间算法是根据M集和J集在复平面上的收敛性提出的，其构造过程如下：

1） 给定计算机屏幕代表的迭代区域W，逃逸半径R及最多迭代次数N。

2） 定义逃逸时间函数

3） 对迭代区域内的点c，计算 T (c)。

4） 如果 T (c )=0，则 c ∈M或J；如果T (c )≠0，则 c∉M或J。

5） 对c点根据一定的渲染技术着色。

基于逃逸时间算法的思想，以下对Julia集和Mandelbrot集的具体算法思想不再赘述。

通过 f (z)=z2+c生成的 Julia集的逃逸时间算法，得到它的图像，图1为 c = 0.1+0.5i的图像，图2为 c=-0.12+0.74i 的图像。

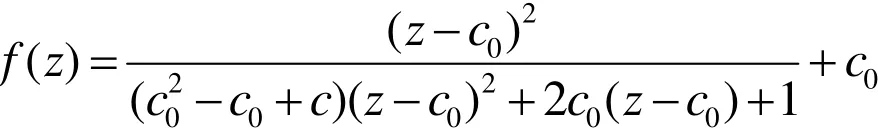
根据定义2可以得出生成的 Julia集的逃逸时间算法，进而得到它的图像。其中图3为 c0=0，c = 0. 1+0.5i 的图像，即的Julia集在 i c 5.01.0+= 时的图像；图4为的图像，即的Julia集在时的图像；图5为 c0= 0.1+0.3i ，c = 0. 1+0.5i 的图像；图6为 c0= 0.1+0.3i ， c=-0. 12+0.74i 的图像；图7为 c0= 0.7+0.1i ， c = 0.1+0.5i的图像；图8为c0= 0.7+0.1i ， c=-0. 12+0.74i 的图像。

观察图3～图8，可以看出图3是图1以0点为中心的反演，图4是图2以0点为中心的反演，图5和图7是图1以 c0= 0.1+0.3i 和 c0=0.7+0.1i点为中心的反演，图6和图8是图2以 c0=0.1+0.3i和c0= 0.7+0.1i 点为中心的反演，进而得出结论的Julia集是 f (z)= z2+c的Julia集以任意定点c0为中心的反演。

图1 Julia集f (z )=z2+c c = 0.1+0.5i

图2 Julia集f (z )=z2+c c=-0.12+0.74i

图3 Julia集 c0 =0 c = 0.1+0.5i

图4 Julia集 c0=0 c=-0.12+0.74i

图5 Julia集c0 = 0.1+0.3i c = 0. 1+0.5i

图6 Julia集 c0 = 0.1+0.3i c=-0.12+0.74i

图7 Julia集 c0 = 0.7+0.1i c = 0.1+0.5i

图8 Julia集c0 =0.7+0.1i c=-0.12+0.74i

由此我们得出：

2.3f(z) = z2+ c及生成的Mandelbrot集

图9为 f (z )=z2+c的Mandelbrot集的图像；图10～15为的Mandelbrot集的图像。其中图10是 c0=0，即的Mandelbrot集的图像；图11为图10的放大图；图12～15中, c0分别取值 0. 1+ 0.2i，0 . 1- 0.2i，0. 7+ 0.1i ,0 .7- 0.1i。

观察图10，我们发现图10是图9以0点为中心的反演。由于 f (z )=z2+c的Mandelbrot集是关于实轴对称的，所以以 0为中心反演后的的 Mandelbrot集也是关于实轴对称，而且芽孢面向内部。观察图11发现芽孢形状类似 f (z )=z2+c的Mandelbrot集。

更进一步的，由图12～图15可以看出，图12与图13二者是关于实轴相互对称的，图14与图15二者亦然。所以我们可以得出结论当c0取两个共轭值时所对应的两个 Mandelbrot集是关于实轴相互对称的。

综上我们可以得出：

图9 Mandelbrot集f (z)=z2+c

图10 Mandelbrot集f(z )= z2+

图11 Mandelbrot集 图10的放大图

图12 Mandelbrot集

图13 Mandelbrot集

图14 Mandelbrot集

图15 Mandelbrot集

3 结 论

[1] 陈 亮, 陈锦昌. 用VB实现Mandelbrot集分形图的研究[J]. 工程图学学报, 2003, (3): 99-104.

[2] 陈锦昌, 张国栋, 陈 亮. Mandelbrot集的内部结构[J]. 工程图学学报, 2004, 25(3): 78-81.

[3] 王兴元, 黄 丽. 广义Mandelbrot-Julia集的内部结构[J]. 工程图学学报, 2005, 26(5): 98-104.

[4] 朱志斌. Mandelbrot集和Julia集关系的初探[J]. 河西学报, 2003, 19(5): 59-61.

[5] 朱志斌. Mandelbrot集和Julia集统一新模型的建立与模拟[J]. 微电子科学与计算机, 2009, 26(10): 217-219.

[6] 焉德军, 张 洪, 朱伟勇. 复迭代z →+c 的Mandelbrot集和 Julia集[J]. 沈阳工业大学学报, 1999, 21(2): 169-171.

[7] 焉德军. 复迭代映射zn+1=+c 的广义Mandelbrot集研究[J]. 应用数学学报, 2001, 24(4): 527-532.

[8] 派特根 H O, 里希特 P H. 分形——美的科学[M].北京: 科学出版社, 1994: 1-100.

The inversion between Mandelbrot and Julia sets

Li Jinfei1, Sheng Zhongping2
( 1. Daqing Petroleum High School, Daqing Heilongjiang 163712, China; 2. School of Mathematics and Statistics, Northeast Normal University, Changchun Jilin 130024, China )

The inversion problem between Mandelbrot and Julia sets is discussed in this paper. Providing the inversions of arbitrary point on extended complex plane to iterative functions, it obtains two kinds of conjugate function of the iterative function drawing Julia and Mandelbrot sets. The Julia and Mandelbrot sets for the two kinds of conjugate function, are exactly the inversion figures of original ones. Using the escape time algorithm, it draws the inversion figures of Julia and Mandelbrot sets.

fractal; inversion figure; escape time algorithm; Julia set; Mandelbrot set

TP 301.5

A

2095-302X (2012)03-0125-04

2010-06-18

国家自然科学基金资助项目（10971022）

李劲菲（1987-），女，内蒙古通辽人，学士，主要研究方向为分形动力系统。