与或功能树的无损简化方法

唐益明， 刘晓平

（1. 合肥工业大学信息与通讯工程博士后科研流动站，安徽 合肥 230009；2. 合肥工业大学计算机与信息学院，安徽 合肥 230009）

与或功能树的无损简化方法

唐益明1,2， 刘晓平2

（1. 合肥工业大学信息与通讯工程博士后科研流动站，安徽 合肥 230009；2. 合肥工业大学计算机与信息学院，安徽 合肥 230009）

当前概念设计中较大规模功能树存在解空间庞大、冲突定位困难的问题，对此提出基于与或功能树的无损简化方法。证明了无损收缩简化、无损删除简化、无损提取简化的相关定理，并籍此给出与或功能树的无损简化算法。最后通过实例，证明该算法可在保持逻辑等价和创新能力不损失的前提下有效降低问题的复杂度，从而提高了概念设计的效率。

计算机应用；概念设计；无损简化；与或功能树

产品设计是一个复杂的创造性生产过程，其中概念设计是产品设计过程中最初的也是最具创造性的阶段[1-2]。而“功能”这个概念贯穿概念设计的各个阶段，它是概念设计的最基本元素[3-4]。一般概念设计主要可以划分成两个阶段：第一，功能分析，确定某个抽象层次的功能，分解功能，建立功能树和功能结构，这里往往也涉及功能树的优化（比如简化）问题；第二，功能求解，对每个分功能进行求解，得到分功能原理解，并组合形成设计方案。

与或非功能树是一种应用广泛的功能分析方法。文献[5]中建立了需求域-功能域-原理解域循环映射的概念设计模型，并提出了概念设计与/或树形式化表达方法。文献[6]中将行为域引入到公理化设计，采用功能-行为-载体（结构）的域结构模板，并通过功能层、行为层、载体层交替出现的与或功能树来实现。文献[7]中提到基于公理化设计，将功能域向结构域的曲折映射表示为产品结构树，只是该树仅涉及到“与”分解。作者在文献[8]中针对与或功能树，基于布尔代数理论提出了一种基于功能集族的功能求解方法。文献[9]基于相似理论和可拓学理论，针对与、或、非分解的功能树进行相似扩展研究。

功能树的方案数通常通过组合原理来获得[10]。但对于规模较大的功能树，其结构的复杂性就难以让设计者理清头绪，而且其功能的实现方案数往往较庞大，导致很难准确寻找出最优解；同时，作为概念设计的本质，创新推理的主要难点在于冲突的检测、定位与消解[11-13]。但对于规模较大的功能树，组合求解所得到的庞大解空间，使得设计者很难迅速发现并定位冲突所在，更难以消解冲突。因此，如果能对功能树进行简化，将其中的冗余去除，使得树的规模等价地减小，将会使得这一系列问题得到极大缓解。为此，作者在文献[14]中利用布尔表达式和功能树的特点，提出了基于布尔代数理论的与或功能树的逻辑简化策略。

但是，经过更深一步的研究，作者发现：利用布尔代数理论进行逻辑简化会造成设计解空间的损失。具体而言，创新推理的设计解可以用简单合取式[15]的形式来表示（如x1∧ x2∧ … ∧xk），而每一个布尔变量，就代表问题的一个原子解。因此，一旦损失布尔变量，就意味着损失了解决问题的一大批方法；甚至损失了最好的解。利用布尔代数来对功能树进行逻辑简化，有可能会造成解空间的损失。

为此，本文提出了无损简化的思想。由于与或非功能树的无损简化极其复杂，因此本文仅针对与或功能树的无损简化问题进行研究。首先介绍与或功能树的基本定义，然后给出了几个无损简化定理，并籍此给出与或功能树的无损简化算法，最后通过具体的实例，验证了该方法的有效性。

1 与或功能树的基本定义

与或功能树可视为布尔代数理论的一种应用[11]。“与”门分解相当于“∧”，“或”门分解相当于“∨”。对于功能T，若按或门展开为 A1和A2，则有 T = A1∨ A2，即功能 A1或 A2实现，则有功能T实现，其余类似可得。为了方便，顶节点为 G1的与或功能树记为 H(G1)。

定义1 对于与或功能树 H(G1)中重复的叶子节点，称其为基本变量，记为 xi。当基本变量 xi对应叶子节点的需求实现时 xi取1，否则取0。类似地，将功能树中门节点用 Gj表示，称为扩展变量。基本变量和扩展变量统称为树变量。H(G1)中出现的所有基本变量下标的集合，记为V(G1)。

定义 2 定义布尔函数 φ( X) = φ(x1,…, xn,G1,… ,Gp)为与或功能树 H(G1)的树函数（ n,p分别为树的基本变量数和扩展变量数），若功能树对应总需求实现时φ ( X)取 1，否则取0。如果树函数仅含有基本变量，则称为目标树函数。对功能树自上而下，通过与、或展开，直至叶子节点，可得目标树函数。

例1 图1为与或功能树的一个示例，其目标树函数φ (X ) = φ(x1,…,x6,G1,…,G5)=G1= G2∨G3=(x1∧G4∧x2)∨(x4∧ G5)=[x1∧(x1∨x3)∧x2]∨[x4∧ (x5∨ x6)]。并且 V(G1)= {1,2,… , 6}。

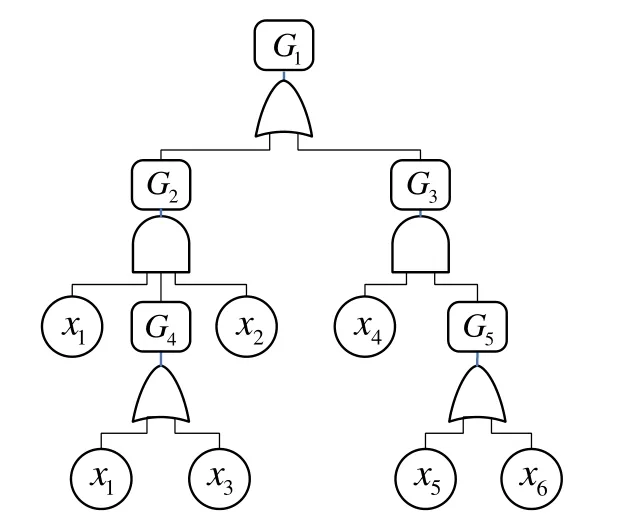
图1 功能树示例

2 与或功能树的无损简化方法

2.1 无损简化定理

定义3 设与或功能树 H(G1)相应的V(G1)= {1,2,… ,n}，对 H(G1)基于布尔代数理论进行逻辑简化后得到 H '(G1)，如果 H '(G1)对应的基本变量集合为 {x1,x2,… ,xn}，则称此逻辑简化为无损简化。也称 H'(G1)是 H(G1)的无损简化。

定理 1 （无损收缩简化） 以下操作均为无损简化：

1） 如果相邻两层门类型相同，合并这两个门为一个门。

2） 在同一个门的输入中，合并相同的基本变量。

3） 如果一个门只有一个输入，删除这个门，其输入上移。

证 明 第一，由 xi∨ (xj∨ xk)=xi∨xj∨xk，xi∧ (xj∧ xk)= xi∧ xj∧ xk，以及定义3，可得结论成立（此时基本变量集合显然未发生变化）。第二，由 xi∨ xi= xi，xi∧ xi= xi，以及定义3，可知结论成立。第三，从功能树的分解角度来看，不妨设为“与分解”，则父节点仅扩展为一个子节点，显然父节点的逻辑状态与子节点相同，此时删除该门，并将输入上移，对功能树的逻辑结构没有本质影响。由定义3，可得结论成立。证毕。

定义4 将功能树的某节点 xi所在的层数记为L(xi)。规定顶节点 xi的层数为 L(xi)=1，且对于 xi的直接孩子节点 xj，有 L(xj) = L(xi)+1。依次类推，形成各层的层数。

定义 5 定义门变量 Gi的所有直接孩子节点序号构成的集合为门变量 Gi的展开，记为 Pi。如果 Gi的直接孩子节点中没有重复的基本变量节点，Pi直接为 Gi孩子节点序号的集合；如果 Gi的直接孩子节点中有重复的基本变量节点，如有多个 xi，则将其依次编号为 i(1),i(2)等归入 Pi中。

例 2 在图1中，为了区分，令功能树中第3层出现的 x1为 x1(1)，而第4层的 x1为 x1(2)。则L(G1)=1，L (G2) = L(G3)= 2，L (x1(1)) =L(G4) = L(x2)= 3。对于定义5，需要对门节点重新编号，比如 G1,G2,G3,G4,G5可依次重新编号为x7,x8,x9, x10,x11，则对于 G1，相应的P1= {8,9}；对于 G2，相应的 P2= {1,10,2}。

定义6 如果与或功能树满足如下特征：门的类型隔层相同，分别为“与—或—与—或—…”，或者为“或—与—或—与—…”，则称为AND/OR树。其中，按树的顶节点为与门、或门，分别称为AND-OR交错树、OR-AND交错树。

由定理1不难得到以下命题：

命题1 对于与或功能树 H(G1)，对其进行无损收缩简化后得到 H '(G1)，则 H '(G1)为AND/OR树。

对于与或功能树 H(G1)，对于其中的任一基本变量 xi,记 NG1(xi)为基本变量 xi的出现次数。

定理2 （无损删除简化1） 如果在AND/ OR树的某个门 G1下有基本变量 xi，同时，在以G1为顶的子树的偶数层上的某个门 G2下也有xi，即 L(G2) - L(G1) ≡ 1(mod2)，且 PG1∩PG2⊇{i}，若对 ∀j ∈ V (G2)，有 NG2(xj)＜ NG1(xj)，则在删除门 G2为顶的子树后，得到的H'(G1)是 H(G1)的无损简化。

证 明 无妨设 H(G1)是AND-OR交错树，即 G1是个与门，令 k=L(G2) -L(G1)≡1(mod2)。为了方便，对某节点 Gi的或展开，可将 Pi对应的节点拆成两个部分A和B，即 A∪B ={xj| j∈Pi}，令不致混淆时，可简记为 TGi。同理，对 Gi的与展开令，简记为 SGi。设 G1,Gt1,Gt2,…,Gtk-1,G2为展开后含 xi的自上而下的门序列，且

显然，Gt1,Gt2,Gt3,…,Gtk-1,G2分别为或门、与门、或门、与门、…、与门、或门。

归纳法。当 k= 1时，有

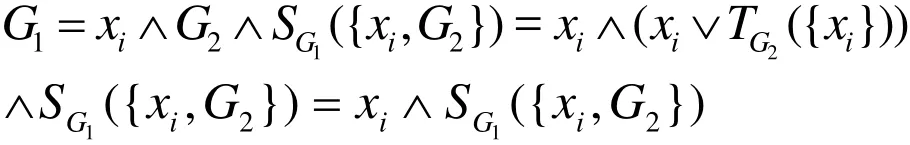
注意到对 ∀j∈ V(G2)，有NG2(xj) ＜ NG1(xj)，则在删除门 G2为顶的子树后，得到的 H '(G1)中的基本变量集合不变，由定义3可知结论成立。现假设 k= L(G2) - L(G1)=2 ×n -1(n ≥1)时定理成立。则当 k = 2 × n+ 1时，有

现令 G3=xi∧ Gt3∧ SGt2({Gt3})，由于G3是Gt3的父节点，则有 L(G3) = L(Gt3)-1 = L(Gt2)，则L(G3)- L(G2)= 2 × n -1。则由假设，此时定理得证。至此，由归纳法可知，整个定理证明完成。证毕。

定理3 （无损删除简化2） 如果在AND/OR树的某个门 G1下有基本变量 xi，同时，在以G1为顶的子树的奇数层上的某个门 G2下也有xi，即 L(G2)- L(G1) ≡ 0(mod2)，且 PG1∩PG2⊇{i}，则在删除门 G2的孩子节点 xi后，得到的 H'(G1)是 H(G1)的无损简化。

证 明 无妨设 H(G1)是AND-OR交错树，即 G1是个与门，令 k= L(G2)- L(G1)≡0 (mod2)。相关假设类似于定理 2。设G1,Gt1,Gt2,…,Gtk-1,G2为展开后含 xi的自上而下的门序列，并且

显然，Gt1,Gt2,Gt3,…,Gtk-1,G2分别为或门、与门、或门、…、或门、与门。

归纳法。当 k= 2时，有

考察式(1)展开的全过程，注意到其中有且仅有一处吸收操作，其子操作为： xi∧ G2= xi∧(xi∧ SG2({xi} )) =xi∧ (SG2({xi}))，显然删除门G2的子节点 xi，对功能树的逻辑结构没有本质影响，并且基本变量集合未发生变化，由定义3可得此时定理得证。

现假设 k= L(G2)- L(G1)=2 ×n(n ≥1)时定理成立。则当 k=2 ×n+ 2(n ≥ 1)时，有

现令 G3=xi∧ Gt3∧ SGt2({Gt3})，由于G3是Gt3的父节点，则有 L(G3) = L(Gt3)-1 = L(Gt2)，则L(G3)- L(G2)= 2× n 。则由假设，定理得证。至此，由归纳法可知，整个定理证明完成。证毕。

定理4 （无损提取简化） 在AND/OR树中，相同基本变量处在同一层的若干个门中，则将该基本变量提取出来的操作是无损简化。

证 明 令共同的几个基本变量的下标集为P，无妨令 P= {1,2,… ,n}。再设展开后得到这几个基本变量的门节点下标集为Q= {1,2,… ,m}。令这几个门的父节点为G，无妨G为与门，则由AND/OR树的特点可知G1,G2,… ,Gm均 为 或 门 。 那 么 ， 可 得由定义 3可得结论成立。证毕。

2.2 与或功能树无损简化的算法流程

以下给出与或功能树无损简化算法的伪代码，见算法1。其大体思想为：首先将功能树的各个门节点存储在队列FuncQueue之中，其次针对 FuncQueue中门节点对应的子树，利用定理1～定理4依次进行无损简化，其中在执行无损删除简化或无损提取简化前要先执行无损收缩简化（以保证此时功能树为AND/OR树）。在算法1中，Is_Simplified先设为true，队列FuncQueue则先设为空。

算法1 功能树无损简化算法

while (Is_Simplified) {

Is_Simplified = false; pTop = FuncTree->top; //获得功能树的顶门指针

Simplify_LlContract (pTop); //无损收缩简化

while (1) { //直接执行循环，通过后面的break来结束循环

while (pTop != NULL) {

if (pTop是门节点) pTop加入到队列FuncQueue中;

pTop = pTop->nextbrother; }

if (FuncQueue不为空){

m_pGate = FuncQueue的队首元素（出队）;

if (Simplify_LlDeleteFir (m_pGate)) Is_Simplified = true;

//无损删除简化1（如果执行了删除操作，则改变Is_Simplified的状态，以下均类似）

Simplify_LlContract (m_pGate); //无损收缩简化

if (Simplify_LlDeleteSec (m_pGate)) Is_Simplified = true; //无损删除简化2

Simplify_LlContract (m_pGate); //无损收缩简化

If (Simplify_LlExtract (m_pGate)) Is_Simplified = true; //无损提取简化

Simplify_LlContract (m_pGate); //无损收缩简化

pTop = m_pGate->firstchild; }

else

break; }

}

3 实 例

图2为一个磁悬浮列车概念设计的与或功能树（仅其中磁斥部分），其中ix表示基本变量。运用本文的方法进行无损简化后得到图3，按文献[14]中的逻辑简化方法得到图4。简化数据如表1所示，其中基本变量的冗余程度定义为叶子节点数/基本变量数。

现在分析一下最后得到的结果，对于图3所示的功能树，其树函数等价于（得到的方案数为7项）

图2 简化前的功能树

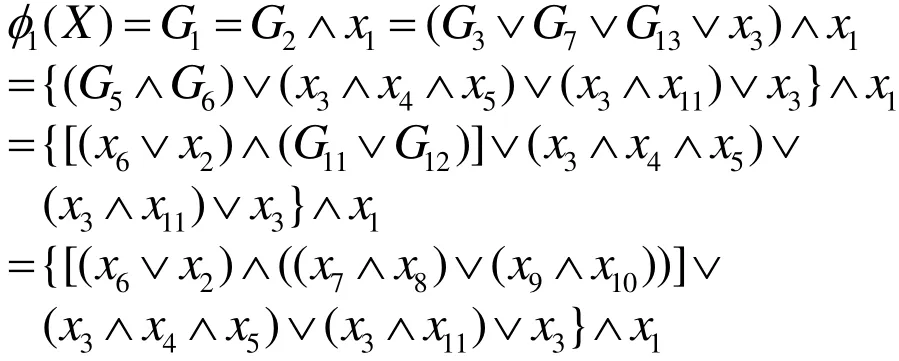
对于图4所示的功能树，其树函数等价于（得到的方案数为5项）

图3 无损简化后的功能树

图4 逻辑简化后的功能树

表1 与或功能树简化数据比较

从当前创新推理的两大主要理论——TRIZ和可拓学出发，可得到创新推理具有如下特征[12-13]：一是创新推理的本质在于对冲突（或矛盾）的处理，而那些不存在冲突的问题，或采用折衷的方法解决问题就不是创新；二是利用基本变量及其之间的关系进行创新推理，进行问题和解的转化，最终得到满足问题的解。因此，冲突和基本变量在创新推理中处于核心地位。在与或功能树中，主要考虑基本变量的要素。而冲突往往需要在与或非功能树中才能得到清晰表达，这将在以后进一步研究。

从这个实例可见：逻辑简化导致基本变量损失的比例高达27.3%，使得部分设计方案丢失，从而削弱了此功能树的创新能力。比如，在图2中的设计方案{x1, x3, x11}（关于如何进行功能求解，请参见文献[8-10]），从φ2(X)可以看出该方案无法通过图4来得到（因为图4中没有出现基本变量x11）。

但是，无损简化保留了所有的基本变量，使得原功能树的创新能力得以无损失的保留。比如同样对于图2中方案{x1, x3, x11}，在图3中就可得到（从φ1

(X)可知）。从而无损简化在保持逻辑等价和创新能力不损失的前提下有效降低了问题的复杂度，对于提高概念设计的效率有着直接的推动作用。

4 总 结

针对当前概念设计中较大规模功能树存在的问题，提出与或功能树的无损简化方法。该方法可在保持逻辑等价和创新能力不损失的情况下对功能树进行简化，能够有效缩减解空间，对于冲突发现与定位起到积极的推动作用，从而提高了概念设计的效率。本文的研究仅针对与或功能树，而对于与或非功能树，其既需要考虑基本变量，又需要分析冲突因素，从而使问题变得极其复杂。进一步地，文献[8-10]等在功能求解的同时，都伴随着简化的因素；这里的简化是否也存在损失的问题；若存在，则又如何避免损失？这些问题都将成为以后的工作重点。

[1] Shai O, Reich Y, Rubin D. Creative conceptual design: extending the scope by infused design [J]. Computer-Aided Design, 2009, 41(3): 117-135.

[2] Hsu W, Irene M Y W. Current research in the conceptual design of mechanical products [J]. Computer-Aided Design, 1998, 30(5): 377-389.

[3] Stone R, Wood K. Development of a functional basis for design [J]. Journal of Mechanical Design, 2000, 122(4): 359-370.

[4] Chakrabarti A, Thomas P B. A scheme for functional reasoning in conceptual design [J]. Design Studies, 2001, 22(6): 493–517.

[5] 张 帅, 冯培恩, 潘双夏, 等. 基于循环映射模型的概念设计自动化策略研究[J]. 计算机辅助设计与图形学学报, 2005, 17(3): 491-497.

[6] 宋慧军, 林志航. 公理化设计支持的概念设计产品模型[J]. 计算机辅助设计与图形学学报, 2002, 14(7): 632-636.

[7] 朱龙英, 朱如鹏, 刘正埙. 公理化设计与DFA集成的产品信息模型[J]. 计算机辅助设计与图形学学报, 2004, 16(2): 216-221.

[8] 秦 晋, 刘晓平. 基于功能集族的功能求解方法[J].工程图学学报, 2008, 29(5): 12-17.

[9] 刘晓平, 陆劲挺, 唐益明. 基于可拓学的对比相似功能树扩展方法[J]. 工程图学学报, 2009, 30(1): 153-159.

[10] 刘晓平, 唐益明, 秦 晋, 等. 概念设计中基于扩展功能矩阵的功能求解方法[J]. 计算机辅助设计与图形学学报, 2007, 19(12): 1610-1617.

[11] Tang Yiming, Liu Xiaoping. Task partition for function tree according to innovative functional reasoning [C]//Proceedings of CSCWD 2008, China, 2008: 189-195.

[12] 刘晓平, 唐益明, 秦 晋. 基于TRIZ的计算机辅助创新原型系统的研究与实现[J]. 工程图学学报, 2007, 28(6): 6-11.

[13] Liu Xiaoping, Qin Jin, Tang Yiming. An innovative function-tree building method based on similarity theory and extension theory[C]//Proceeding of CAID&CD’06, Hangzhou, China, 2006: 199-204.

[14] 路 强, 刘晓平. 基于布尔代数的功能树简化研究[J].合肥工业大学学报(自然科学版), 2009, 32(7): 1025-1029.

[15] Gaur D R, Krishnamurti R. Self-duality of bounded monotone boolean functions and related problems [J]. Discrete Applied Mathematics, 2008, 156(10): 1598-1605.

A lossless simplifying method of and/or function tree

Tang Yiming1,2, Liu Xiaoping2
( 1. Information and Communication Engineering Postdoctoral Research Station, Hefei University of Technology, Hefei Anhui 230009, China; 2. School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China )

Aiming at huge solving space and difficult conflict-orienting for large-scale function tree in conceptual design, a lossless simplifying method of and/or function tree is proposed. Some lossless simplifying theorems related to contract, deleting and extracting are proved, and then the lossless simplifying algorithm of and/or function tree is given based on these theorems. Finally, experimental results show that the algorithm can effectively reduce complexity holding logic equivalence and lossless innovative ability, and improve the efficiency of conceptual design.

computer application; conceptual design; lossless simplifying; and/or function tree

TP 391.72

A

2095-302X (2012)03-0034-07

2010-05-05

国家自然科学基金资助项目（61105076，61070124，90920006）

唐益明（1982-），男，安徽无为人，讲师，博士，主要研究方向为模糊逻辑，CAD，情感计算，仿真与可视化。