预应力在施工阶段中对曲线连续刚构桥的影响分析

肖 荣，王 超

(重庆市建筑科学研究院，重庆400020)

预应力在施工阶段中对曲线连续刚构桥的影响分析

肖 荣，王 超

(重庆市建筑科学研究院，重庆400020)

该文以达陕高速泥溪沟2号大桥——曲线连续刚构桥为工程依托，建立该大桥的三维板单元模型。通过对计算数据的分析，得到预应力钢束对不同曲线半径连续刚构桥梁的变形以及受力的影响，并且总结了相应的变化规律，为今后此类桥梁的设计与施工提供参考。

板单元模型；计算数据；预应力钢束；连续刚构桥

1 预应力布置

该文以达陕高速泥溪沟2号大桥连续刚构桥为背景进行研究。大桥单幅以中跨跨中截面对称分布，半桥节段划分及预应力空间分布如图1所示。

图1 纵向预应力钢筋布置图

2 预应力钢筋作用原理

采用Midas FEA软件中自带的四边形板单元对混凝土结构进行模拟计算[1]。该文在板单元中插入的是杆式钢筋，Midas FEA软件中其作用原理为：在曲板单元的杆式钢筋有两节点或三节点钢筋。杆式钢筋位置由钢筋节点决定。通过前处理过程钢筋被分割成钢筋段。每个钢筋都属于各自的母单元。钢筋线可定义为空间曲线，由两个钢筋线组成的钢筋。第一个钢筋线是由两个点构成的直线钢筋线，第二个钢筋线是由三个钢筋节点组成的高阶曲线钢筋线。每个钢筋线在穿越板单元网格时会生成交点，即钢筋段定位点。钢筋线由这些定位点被分割成钢筋段。曲线钢筋线被分割成高级钢筋段。各定位点在相应板单元的中性面可以有沿单元坐标轴z方向的偏心。偏心信息是钢筋在板单元中的实际位置的信息。

3 施工阶段预应力对桥梁的影响分析

由于悬臂施工阶段结构为静定体系，且悬臂上只受负弯矩，目前设计中通常只配置顶板预应力束和竖向预应力。在施工过程中最大悬臂阶段是应力最不利工况，因此计算取悬臂最长工况进行[2]。

3.1 竖向位移分析

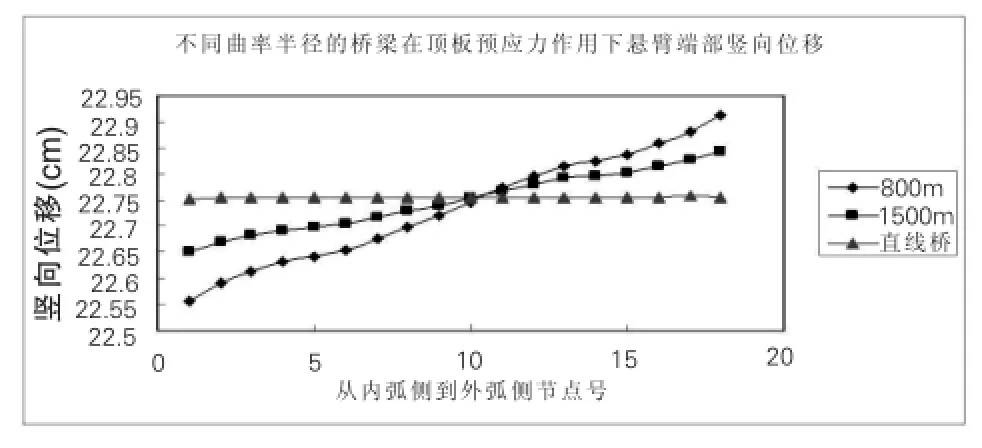
图2 悬臂端截面顶板竖向位移

图3 悬臂1/2截面顶板竖向位移

从图2～3可以看出在设计预应力钢束作用下：

（1）分析沿桥梁纵向各个截面的竖向位移值（以曲线半径为800m的桥梁作为研究对象），发现悬臂端截面和悬臂1/2截面外侧的上翘值分别为22.9cm和6.36cm。表明竖向位移由悬臂根部到悬臂端部逐渐增大。究其原因在于，曲线连续刚构桥中存在初弯矩及弯扭耦合效应。

（2）箱梁的设计预应力钢束产生了初扭矩，致使箱梁梁体发生了偏向曲线内侧扭转。就曲线半径是800m的曲线连续刚构桥而言，悬臂端部截面与1/2截面，其截面内侧和外侧高差分别为0.4cm和0.1cm。

（3）曲率半径愈小，截面内外弧侧差值愈大；当曲线半径足够大时与直线桥梁的扭转效应一致，说明曲线半径越大，越接近直线桥的计算结果。但是曲线桥和直线桥的差值在0.3cm以内。

（4）对计算数据进行总结：直线悬臂刚构与曲线悬臂刚构均呈现悬臂端部高于悬臂根部的上拱现象。800m曲线半径桥梁悬臂端截面的上拱值为22.9cm，直线桥端部截面的上拱值为22.74cm。

3.2 扭转角分析

该文中的扭转角指的是顶板翼缘板的内外两侧竖向位移的差值与梁宽的比值规定向曲线内侧转为正，向曲线外侧转为负[3]。

图4 悬臂端部到根部各截面扭转角分布

图5 桥梁纵向扭转角分布图

从图4～5中可以看出，在对称配置顶板预应力束作用下：

（1）自重使箱梁产生了与顶板预应力束产生的扭转角方向一致的扭转，二者共同使梁体产生了向曲线内弧侧的扭转。自重在悬臂端部截面产生的扭转角为0.6°，而预应力产生的扭转角仅为0.05°，可见自重产生的扭转角比预应力束产生的扭转角大得多，相差12倍。

（2）扭转角纵向上的分布规律是相同的，不会随曲线半径的变化而变化。但是值得注意的是随着曲线半径的减小，相同位置截面的扭转角也越大。所计算模型中曲线半径为800m的刚构桥端部截面的扭转角最大为0.17°。

（3）当曲线的半径一定时，悬臂T构扭转角从根部到端部逐渐增大。曲线半径为800m的刚构桥两个截面间的扭转角变化值约为0.15°，而直线刚构桥不存在扭转角。

3.3 正应力分析

3.3.1 分析顶板正应力

预应力钢筋在最大悬臂状态引起的悬臂端部，悬臂1/2，及悬臂根部截面的正应力分布曲线如图6～7所示。

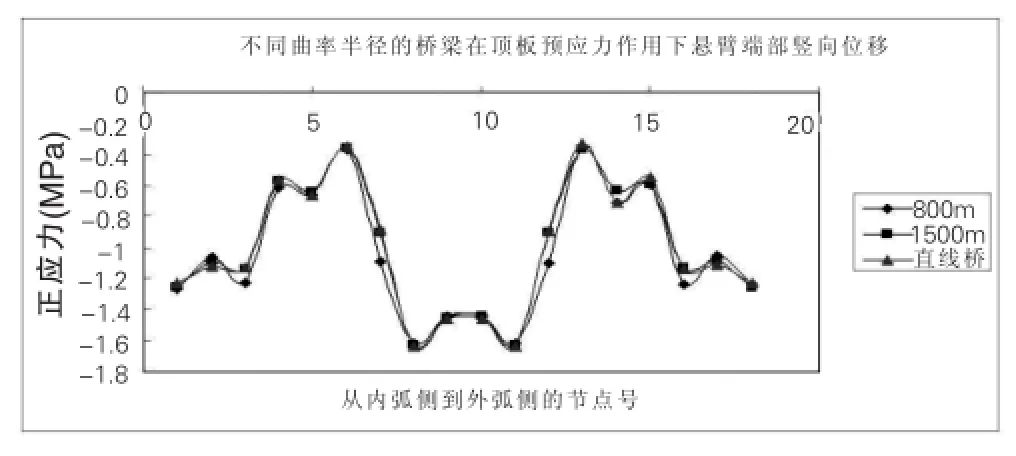
图6 最大悬臂状态端部截面顶板正应力

图7 最大悬臂状态根部顶板正应力分布

从图可以看出:在对称布置预应力束作用下：

（1）800m半径的T构悬臂端部截面的变化区间为-0.34MPa～-1.65MPa，相差1.3MPa。剪力滞现象比较明显。

（2）在预应力钢束的作用下，T构顶板产生压应力最大可达-20MPa，底板大部分承受拉应力最大可达5MPa。值得注意的是，底板上的最大拉应力出现在固结墩和主梁交界处，根据分析是应力重分布的原因，设计时应对该区域进行局部加强。

（3）沿桥跨方向上，顶板的正应力分布规律是由悬臂端部到悬臂根部顶板压应力越来越大。就直线桥而言，端部截面最大正应力为-1.64MPa，悬臂1/2截面最大应力为-13.65MPa，墩顶截面处最大可达-20.61MPa。

3.3.2 顶板剪力滞效应分析

剪力滞系数的定义:上顶板和下底板的正应力值沿顶底板宽度积分，然后除以上顶板和下底板的宽度，得到一个平均正应力，再运用这个平均值去除各点的实际应力值，即得各点的剪力滞系数[4]。

从图8～9可见，对称布置的顶板预应力钢束是结构产生如下结果：

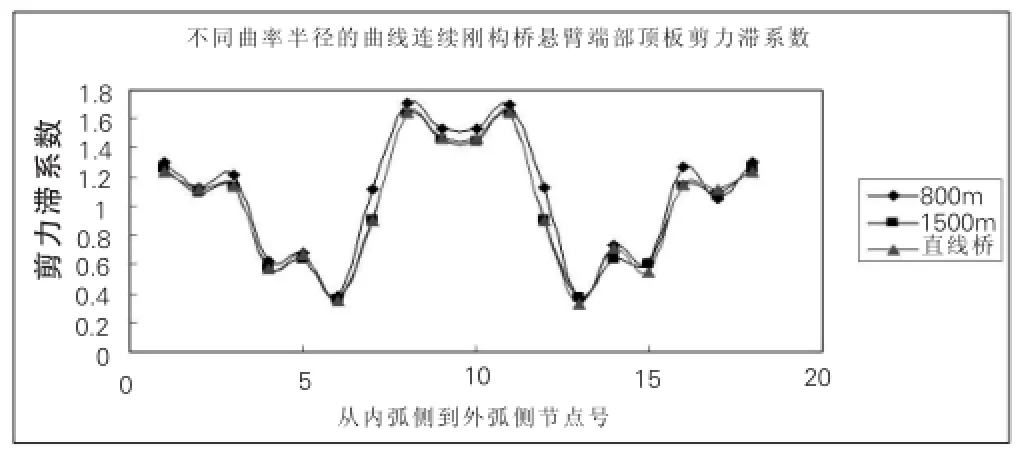
图8 端部截面最大悬臂状态剪力滞

图9 根部截面最大悬臂状态剪力滞

（1）当曲线半径≥800m时，剪力滞系数之大小几乎不随曲线半径的变化而变化。由于弯扭耦合作用的存在使得悬臂根部截面内弧侧比外弧侧剪力滞系数大。但是内外侧剪力滞系数相差仅为0.03。

(2)在顶板横向上剪力滞系数的分布规律为：腹板附近剪力滞系数小于1；截面中点附近及翼缘板上剪力滞系数大于1。即施工阶段预应力束产生的是负剪力滞效应。沿桥梁纵向上，最大剪力滞系数的位置发生了变化：靠近端部截面最大剪力滞出现在两肋板中间；靠近悬臂根部的截面最大剪力滞系数将出现在翼板上。

(3)悬臂根部截面、悬臂1/2截面、悬臂端部截面的最大剪力滞系数分别为1.03、1.04、1.7。由前述三个数值发现，在桥跨方向上剪力滞系数由悬臂根部到悬臂端部逐渐减小。更深入分析得出从端部到1/2截面数值变化较大，但是从悬臂1/2截面到根部截面变化较小的结论。

4 实际工程应用成果分析

应用研究的成果对某大桥实施了施工过程的监控。在施工过程中综合分析自重、预应力、收缩徐变、二期恒载及活载对桥梁的作用，在此基础上对施工过程中桥梁的线形和应力做了科学的预测。其中对预应力在施工阶段中对曲线连续刚构桥的深入研究和探讨，成为促进大桥成功合拢的决定性因素。首先定性的分析了变形和受力在桥梁纵向和横向的分布规律，使得施工控制工作有了着重点。再次定量地给出了大桥施工过程中准确的变形值，这对大桥的线形控制及最终合拢起到关键性的作用。而且事实证明施工过程中大桥的应力状态和该文研究结果基本一致，这就为提前预测下一阶段施工后的应力水平提供依据，保证施工过程安全有序的进行。

5 结束语

目前多采用杆系单元对曲线梁进行研究，这种单元不能充分体现箱梁横向上应力的变化规律，对于变截面曲线连续刚构桥的研究还存在不足；预应力对该种桥型的空间受力影响更是缺乏系统的研究；该文从实际出发，详细探讨了在施工阶段预应力对该种结构受力和变形的影响，得出了有意义的结论。

[1]王超.曲线连续刚构桥空间受力分析[D].重庆:重庆交通大学，2011:45.

[2]吕昌武.高墩大跨曲线连续刚构空间受力分析与施工控制[D].西安:长安大学，2006:31.

[3]马保林.高墩大跨连续刚构桥[M].北京:人民交通出版社，2001.

[4]彭大文.连续弯箱梁桥剪滞效应分析和实用计算法研究[J].中国公路学报，1998，11(3):41-49.

责任编辑:李 红

The Effect of Prestressing Force on Curved Continuous Frame Bridge in Construction Progress

Based on curved continuous frame bridge,a three-dimensional plate element model of the bridge is set.The authors analyze the effect of prestressing tendon on the transform and internal forces of curved continuous frame bridges with different radius and summarize relevant changing rules. This can provide some reference for the design and construction of such kind of bridge.

plate element model;calculated data;prestressing tendon;curved continuous frame bridge

U446

A

1671-9107（2012）07-0035-03

10.3969／j.issn.1671-9107.2012.07.035

2012-05-28

肖荣（1972-），男，四川达州人，本科，助理工程师，主要从事建筑结构检测与加固的研究。

王超（1985-），男，山东临沂人，硕士，助理工程师，主要从事建筑结构检测与加固的研究。