基于DWT数字图像水印技术研究
2012-03-27吴翩卉王春枝
吴翩卉 王春枝
(湖北工业大学,湖北武汉430068)
1.前言
数字水印是一个隐藏信息的行为,它与数字信号的类型(如;图像,歌曲,视频等)有关,它们的概念都是在相应的数字信号里藏有一个信息,然后通过解密来使它们成功分开。水印隐藏的信息与实际的信号的内容有关。
水印算法主要分两种:空间域和变换域。空间域就是把信息嵌入到随机选择的图像点中最不重要的象素位置(Least Significant Bits)LSB,这种水印是不可见的;变换域一般是采用扩展频谱通信技术,它的主要技术有(离散傅里叶变换)DFT,(离散余弦变换)DCT和DWT,根据这些不同的变换,把数字图像转化成相应的频域系数,然后根据它们隐藏的类型进行适当编码和变形,再根据信息量选择频域系数序列,最后将该数字图像中的频域系数的反变换转化为空间域的数据。第二种算法隐藏的信息量不大,但它的抗攻击力好,所以适合版权保护方面的数字水印加密技术。
本文提出了改进的DWT数字水印加密技术,分析此类水印系统的属性,其水印模型将通过MALAB来实现,并通过一些图像的实验来说明这一水印加密技术。
2.提出方法
一个好的水印技术应有高的鲁棒性,也就是不容易被人攻击;另外,有水印的图像应该不容易被去除和宿主图像的质量不应被破坏。
想要得到好的数字水印,首先要研究人眼视觉感知情况,通常图像信息会被人眼分解,并散布到从人眼到大脑视觉皮层的一系列频率带上,并且这些频率带被具有相同特性的图像成分所激活,这使不同频带经过处理后得到彼此间相互的独立。由此,考虑采用DWT对图像进行多尺度的分解,得到在坐标系内相等的一系列频率带,从而保证对不同频带的信息是相互独立,不相互影响。小波分析与人眼视觉系统具有一致性也就是多分辨特性。根据上面说的特点启发了笔者采用小波变换和HVS技术相结合,大大提高了水印的鲁棒性。在图像处理过程中,有时需要将信号在时域和频域中的特性或者图像在空域和频域中的特性结合起来加以分析。比如,要了解图像的哪一部分含有较多的高频分量,传统的傅里叶变换无法解决此类问题。相比之下,DCT是纯粹的空域变换到频率域,因此没有利用图像的空间-频率特性,而这种空间-频率特性正好与人眼的某些视觉特性相一致,也就是说小波变换可以利用HVS的空间-频率特性。其次,采用分块的DCT变换会出现马赛克现象,而用小波变换则不会。因此,离散小波变换不仅可以较好地的匹配HVS特性,而且与JPEG2000、MPEG4压缩标准兼容,小波变换产生的水印具有良好的视觉效果和抵抗多种攻击的能力,因此目前DWT数字水印技术是主要的研究方向。
2.1 离散小波变换(DWT)
小波即小区域的波,又称为子波,是一个长度有限、均值为零的振荡波形。这里的“小”是指衰减性,即局部非零性,非零系数的多少反映了图像块高频成分的丰富程度和纹理的复杂程度;“波”是指波动性,小波变换也可分为连续小波变换CWT(Continue Wavelet Transform)和离散小波变换DWT(Discrete Wavelet Transform)。
小波函数定义:设ψ(t)为一平方可积函数,就是ψ(t)∈L2(R),若其傅里叶变换ψ(t)满足可容许条件;

我们称ψ(t)为一个基本小波。
对于任意L2(R)空间中的函数f(t)在基本小波下展开,称这种展开为函数f(t)的连续小波变换,即为CWT,其表达式为:
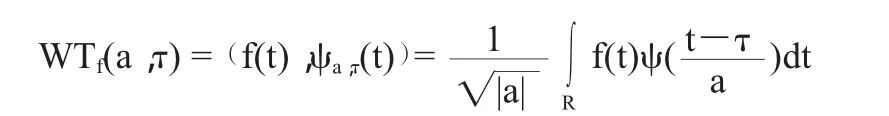
其重构公式(逆变换)为:
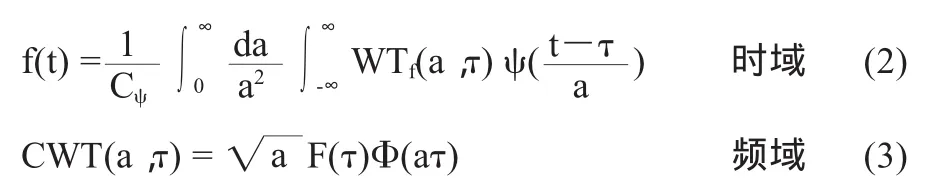
由于连续小波变换的冗余,由一维信号x(t)变换成为二维的WTx(a,r)后,其信息中存在大量的信息冗余。因此从数据压缩和节约计算的角度出发,可将其应用在实际中。通过在离散的尺度和位移下计算小波变换,对位移参数r和尺度参数a用不同的方法进行离散,会得到不同的小波。图像处理中最常用的小波变换为二维小波变换。
二维小波变换的公式为:
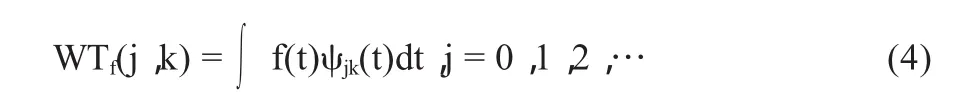
由此可看出小波变换是一种信息保持型的可逆变换,原图像或信号的信息完全保留在小波变换的系数中,小波变换只是使得原图像能量重新分配,这就是小波变换被广泛采用的主要原因。
2.2 DWT和多级分解
二维离散小波变换把图像分解产生一个低频子图LL和三个高频子图:LH、HL和HH,下一级小波变换是在前一级低频子图LL基础上进行的,如此重复三次,即对原始图像进行三级小波分解,分解成十个子图:LL3与LH i,HLi、HHi(i=1,2,3),其中LL3为最低频带子图。分解过程如图1所示。
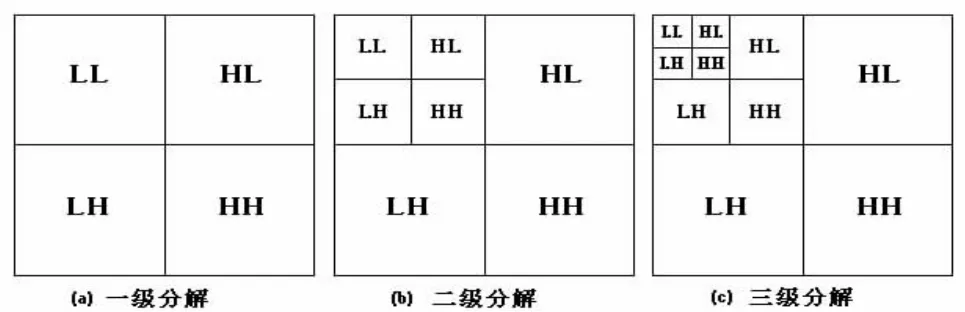
图1 小波分解示意图
a.图像嵌入:
嵌入水印方法如图2:
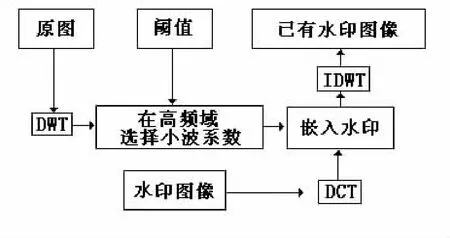
图2 嵌入水印示意图
用DWT二级分解原图X并获得低频子图像和3L的细节子图像(就是高频域)。如何选择DWT的n级别是依赖于主图像和水印信号的大小,越高级数的DWT的分解使得水印嵌入到低频部分就越集中,这样水印的隐蔽性就越差,所以适当分解层数是必要的。而分多少层需要通过改变小波滤波系数集所确定。所以对原图作n级小波变换后,将n级低频参数LLn与水印W(x,y)按强度a叠加,得到有水印图像低频参数LL’n=LLn(1+aW)。最后是按低频参数LL’n做n级小波逆变换,得到F’(x,y).
b.水印提取
由于进行n级小波分解后,第n子图的大小仅为原图像的1/2i。而图像的大部分信息集中在第n级的低频子图内,利用小波重构得到加密图像在一定程度上恢复原图像,很难实现无失真解密;所以在还原的时候一定要注意强度a的取值。

图3 提取水印示意图
从图3可看出恢复图像时要把原始图像F(x,y)、水印后图像F’(x,y)分别做n级小波变换,得到n级低频参数LL’n、LLn,按强度系数a分离出水印W’(x,y)=(LL’n-LLn)/(LLn*a)。
3.实验及结果分析
从定性、定量两方面来展示本算法水印的稳健性和不可感知性。定量方面采用两个常用指标:
相似度NC表示水印图像和原图像的相似度,公式表达式为:
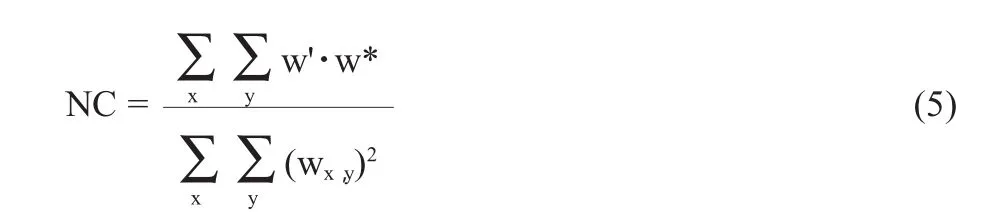
NC取值范围是0到1之间,数值越大水印和原图像的相似度就越高,证明水印图像质量越好。
信噪比PSNR,度量所提取的水印和原始水印的相似度,公式表达式为:
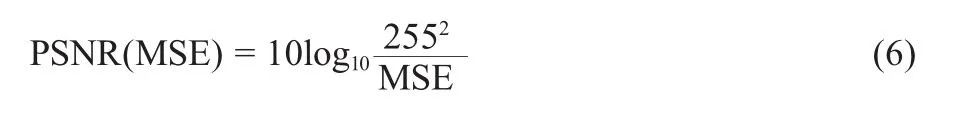
PSNR越大,水印图像的质量就越好。
实验软件是MATLAB,为了验证DWT算法,采用castle.bmp 256×256图像作为水印,选用Haar小波作为三级分解,并嵌入library.bmp 512×512图像作为原始图像,得到加有水印的图像,这样经过版权保护处理的发行物能够测出显示版权保护技术的数字水印如图4所示:
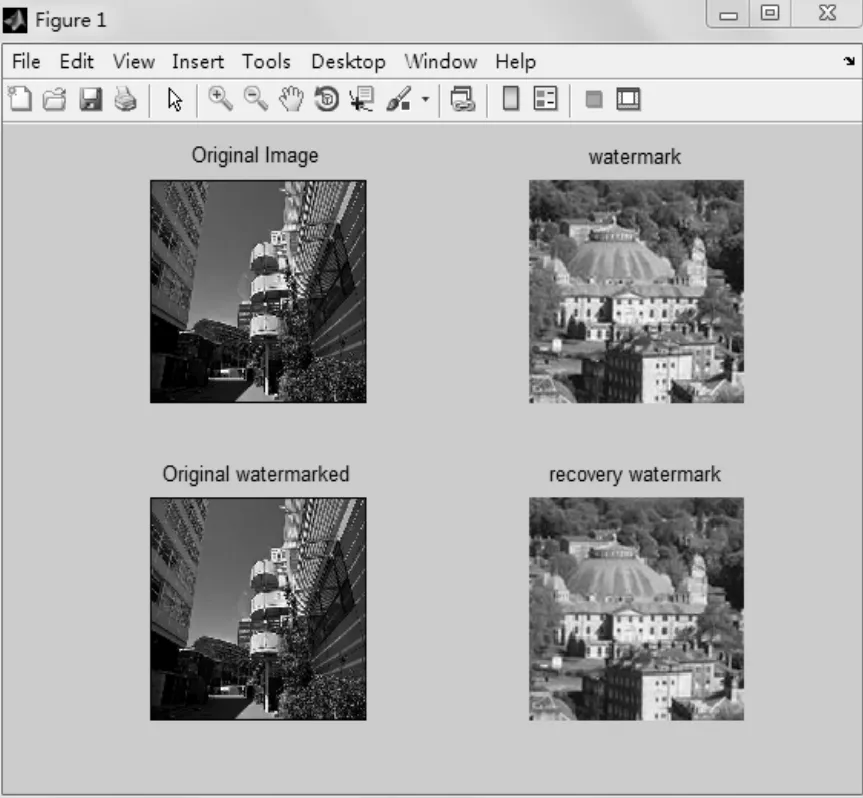
图4 水印图像小波嵌入
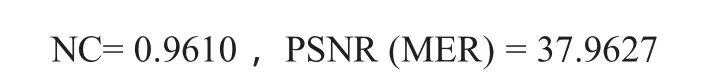
从实验得出的数据可看出,数字图像水印算法是很成功的,而且在保证水印图像的前提下,NC接近于1的强度a,保证了水印的清晰度。
4.总结
本文提出了DWT的盲水印隐藏技术,将二值彩色图像通过调整强度系数嵌入到经小波变换后的原图像的子图上。实验结果表明了此算法具有很强的鲁棒性,既保证了隐藏信息安全性也保护了的原图像的版权,表明了DWT和人眼视觉特性的结合在数字水印技术中具有理论意义和实用价值。
[1] 郭蔚、蔡云飞.一种基于融合的数字图像隐藏技术[J].河北工业大学学报,2003,(32)No.571-75.
[2] Reddy AA,Chatter BN,A new wavelet based logo watermarking scheme[J],Conf Pattern Recognition letters,2005,26(7):1019-1027.
[3] Quan,L.;Jiang,X.(2006):Design and Realization of a Meaningful Digital Watermarking Algorithm Based on RBF Neural Network[J],Proceedings of the Sixth World Congress on Intelligent Control and Automation,WCICA,2006,(1):2878-2881.
[4] 易显东,姚军,唐丹.基于小波变换域的图像加密技术研究[J].信息与电子工程,2005.
[5] 小波分析理论与Matlab7实现.飞思科研发中心编著[M].电子工业出版社,2005.
[6] 李估,付永庆,王咏胜,一种基于模糊聚类的小波图像压缩算法[J].应用科技,2005,32(2):3-5.
