反舰导弹自适应模糊滑模控制系统设计

王朝轰，李增荣，贺建彬

（1.91115部队，浙江 舟山 316000；2.海军装备部驻上海地区军事代表局，上海 200083；3.海军工程大学兵器工程系，武汉 430033）

新型反舰导弹的弹道越来越复杂，在建立其弹道模型时，传统的姿态控制方法已经不能满足设计要求，需要寻找新的途径。尤其是，高低结合弹道的引入使得弹道设计的难度大大增加。然而，过载控制是一种比较简单、可靠的控制方法，更为适用于新型反舰导弹。

文献[1]将神经网络应用于自适应反馈线性化非线性系统；文献[2]利用神经网络控制未知动态特性的非线性系统；文献[3]运用动态逆的双阶段设计方法设计了导弹的逆控制器，并利用有效信息对逆控制器进行在线补偿，实现了对导弹的控制；文献[4]提出了一种基于神经网络的导弹鲁棒动态逆控制方法，利用RBF神经网络逼近导弹慢模态数学模型，鲁棒控制器用于减弱模型不确定性及神经网络的逼近误差对跟踪精度的影响，该控制器设计可以保证闭环系统的稳定性。文献[5-6]运用自适应模糊滑模设计，对导弹末端机动引导律进行了探讨，仿真表明了其方法的正确性和有效性。但文献[1-4]诸方法虽然达到了预期的效果，但本质上都属于姿态控制方法。相对于过载控制方法，传统姿态控制方法使导弹机动性能变差。因此，直接对导弹过载进行控制的过载控制方法将有利于提高导弹的机动能力。

本文针对反舰导弹的过载控制系统设计问题，提出了一种自适应模糊滑模控制系统设计方法。通过Lyapunov 稳定性分析，证明了此闭环系统的所有误差信号均有界且指数收敛至原点的有界邻域内，且仿真结果验证了该方法的有效性。

1 反舰导弹过载控制模型

以气动外形呈轴对称分布的导弹为例，研究其俯仰通道线性动力学模型[7]：

式(1)中：α为迎角；ωz为俯仰角速度；δz为俯仰舵偏角；ny为法向过载；v为飞行速度；g为重力加速度；a22、a24、a25、a34和a35均为导弹的动力系数；Δα、Δzω和Δny均为模型线性化过程中的不确定项。

考虑舵系统的一阶动态特性为：

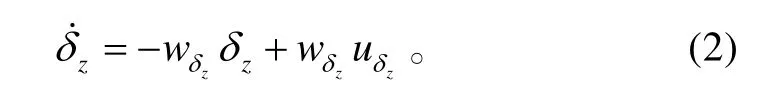
式(2)中：wzδ为俯仰舵系统的带宽；uzδ为控制输入。

进行如下的坐标变换：

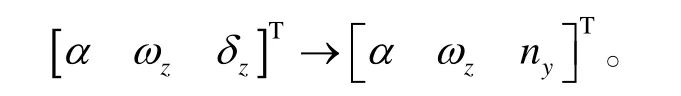
联立式(1)、(2)可得：

针对俯仰通道模型(3)，控制目标为：在给定的法向过载指令 nyc作用下，设计合理的控制律uzδ，使得导弹的实际法向过载 ny跟踪 nyc，且迎角α和俯仰角速度ωz都收敛到理想状态。为了实现此控制目标，将式(3)变换为标准的三角形式，定义可逆的状态变换矩阵T为：

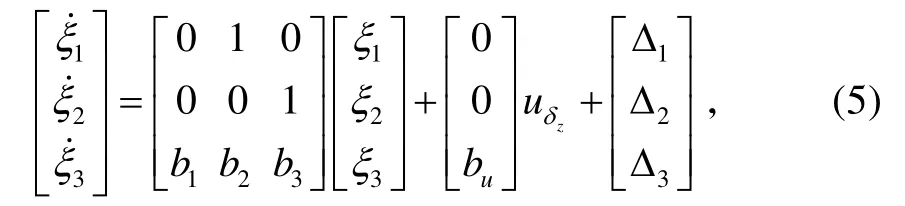
式中各参数的取值参见文献[4]。

由于状态变换矩阵T是可逆的，则系统(5)与系统(3)属于等价变换。以下将针对系统(5)，设计和分析俯仰通道的过载控制系统。

2 反舰导弹过载控制系统设计

2.1 问题阐述

假设1：存在未知的上界值r1、r2和r3，使得系统的不确定项 Δ1、Δ2和Δ3满足：

针对等价变换后的俯仰通道过载控制模型(5)，采用反演设计方法和自适应模糊控制方法进行设计。定义被控对象(5)的状态误差为：

式中，ξ1d、ξ2d和ξ3d为系统期望的状态轨迹，ξ1d由期望的过载信号 nyc滤波得到，ξ2d和ξ3d分别由式(13)、(29)定义。

由式(5)、(7)，可得状态误差的动态方程分别为：

2.2 设计步骤

1)考虑系统(8)，对于期望状态的微分信号ξ1d采用模糊逻辑系统给出[8-11]，采用俯仰通道期望的过载信号 nyc和状态变量α、ωz、ny作为此模糊逻辑系统的输入信号，应用模糊逻辑系统具有的任意逼近能力，估计出信号。

对于期望状态ξ1d的获取，可以直接对微分信号进行积分即可得到。

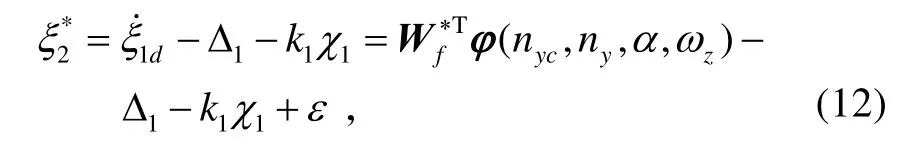
将ξ2作为式(8)的虚拟控制量，则存在一个理想的虚拟控制量：使得其中 k1＞0为设计参数。由于是得不到的，故选取期望的虚拟控制量为：

针对系统(8)，选取Lyapunov函数为：

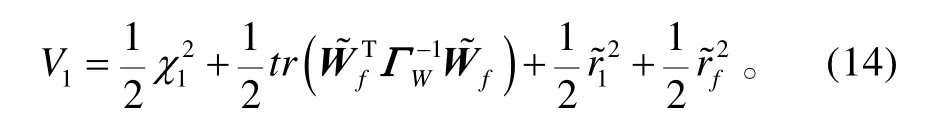
对V1求导，并将式(8)、(11)、(13)代入式(14)，可得：

式中，δW＞0为设计参数。

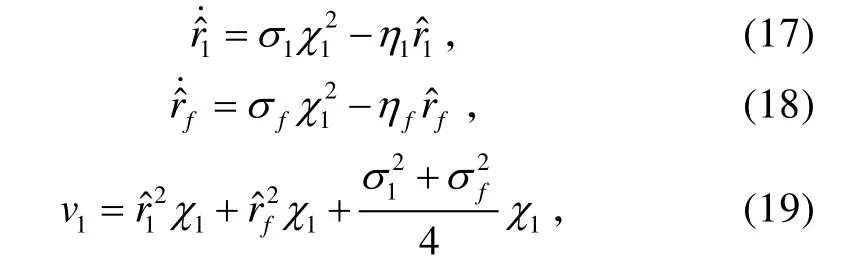
式中，σ1＞0、η1＞0、σf＞0和ηf＞0为设计参数。

将式(16)～(19)代入式(15)，可得：

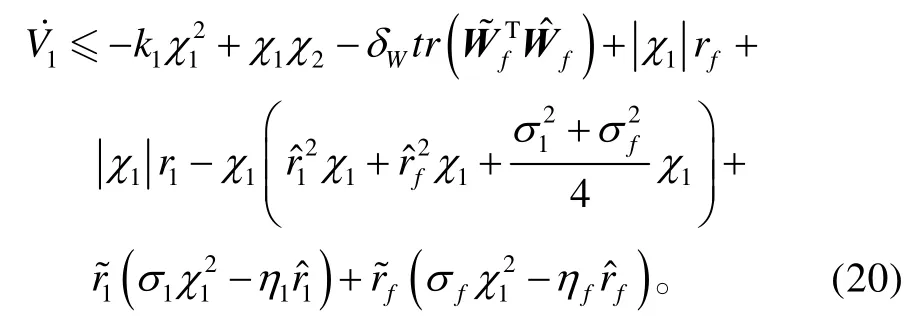
由于

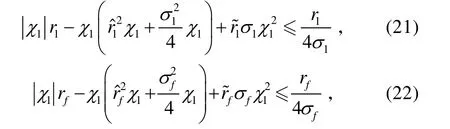
所以，有

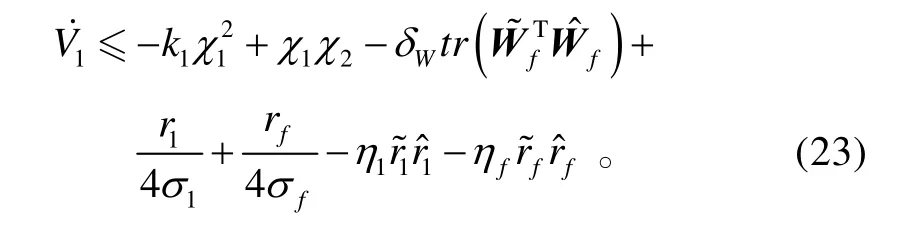
考虑到

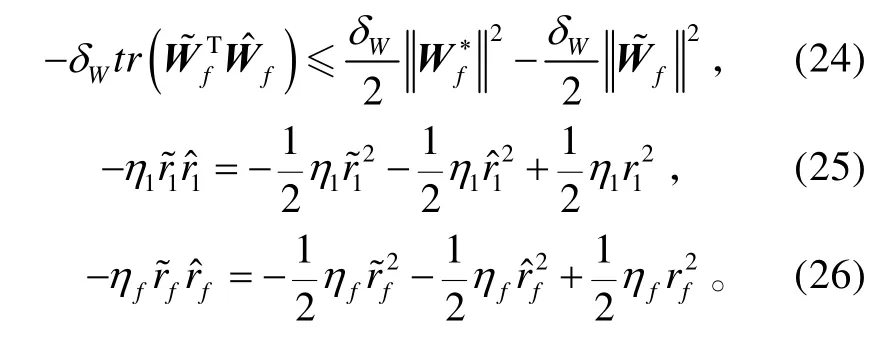
将式(24)～(26)代入式(23)，可得：

2)考虑系统(9)，将ξ3作为式(9)的虚拟控制量，则存在一个理想的虚拟控制量：

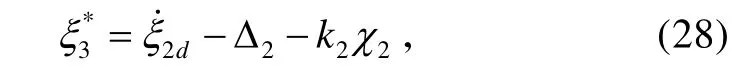
3ξ是得不到的，故选取期望的虚拟控制量为：

式中，v2为引入的鲁棒项，如式(33)所示。

针对系统(9)，选取Lyapunov函数为：

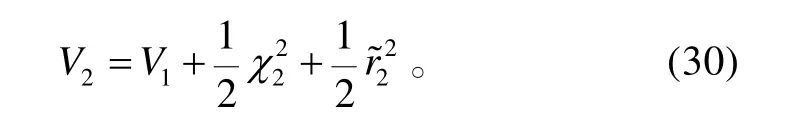
对V2求导，将式(9)代入式(30)，且考虑到假设1，可得：

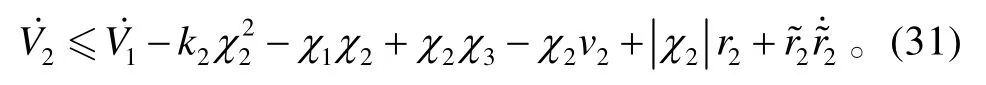
式中，σ2＞0、η2＞0为设计参数。

将式(32)、(33)代入式(31)，可得：

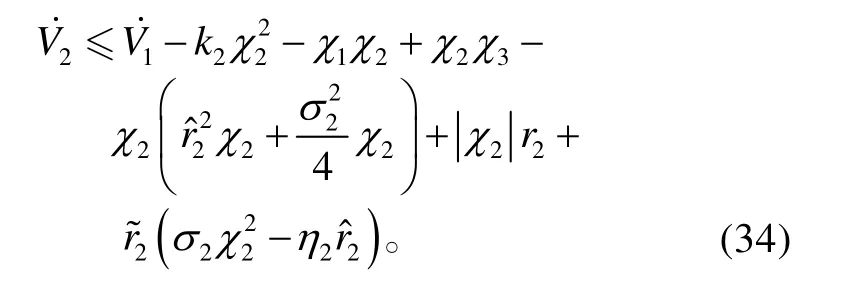
由于

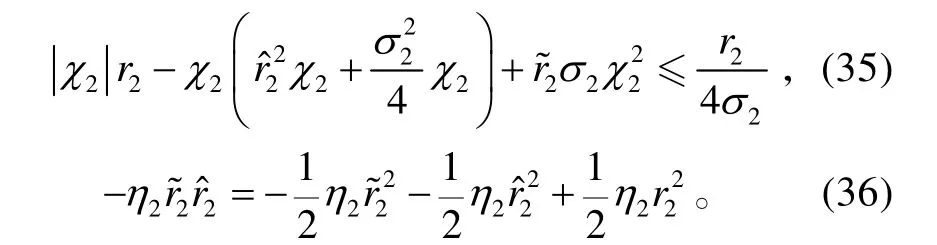
将式(27)、(35)、(36)代入式(34)，可得：

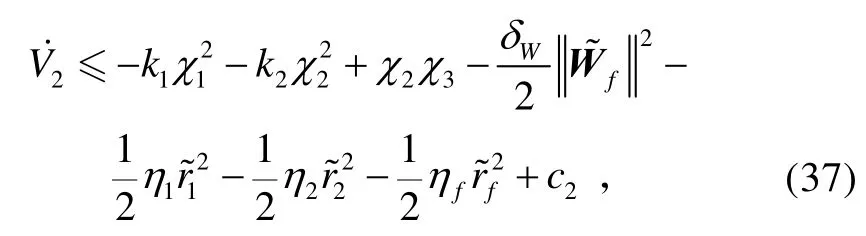
3)考虑系统(9)，其中uzδ为实际控制量，采用滑模控制方法设计控制量uzδ。

设计系统滑模面为：

设计系统的控制量uzδ为：

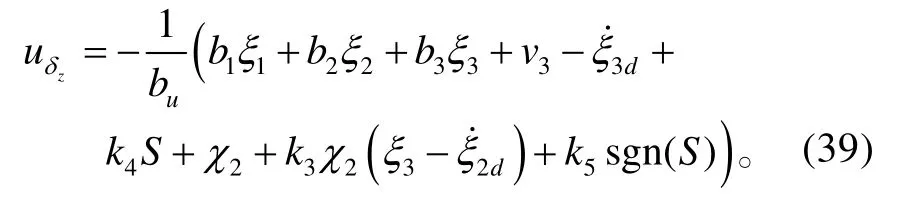
式(39)中：v3为引入的鲁棒项，见式(44)；k4＞0、k5＞0为设计参数；sgn(⋅)表示符号函数。

针对系统(9)，选取Lyapunov函数为：

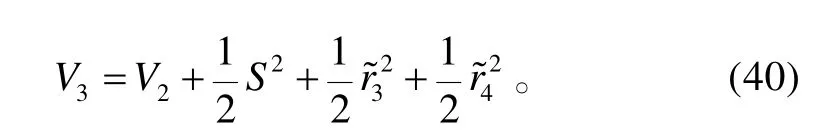
对V3求导，将式(38)、(39)代入式(40)，且考虑到假设1，可得：

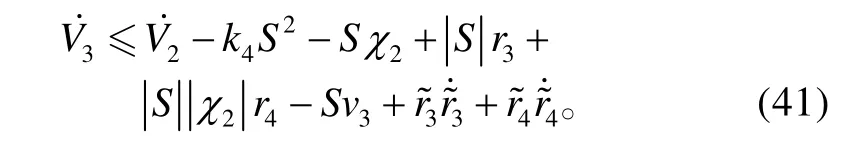
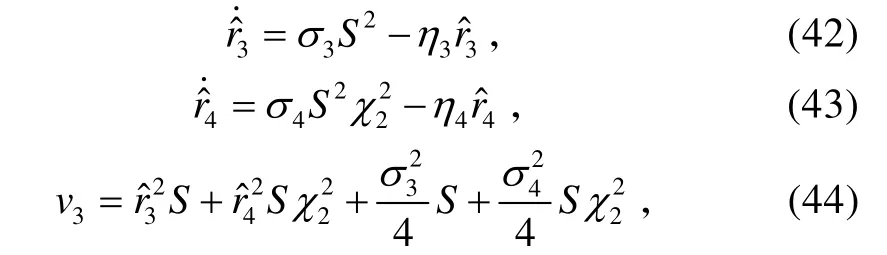
式中，σ3＞0、η3＞0、σ4＞0和η4＞0为设计参数。

将式(42)～(44)代入式(41)，可得：

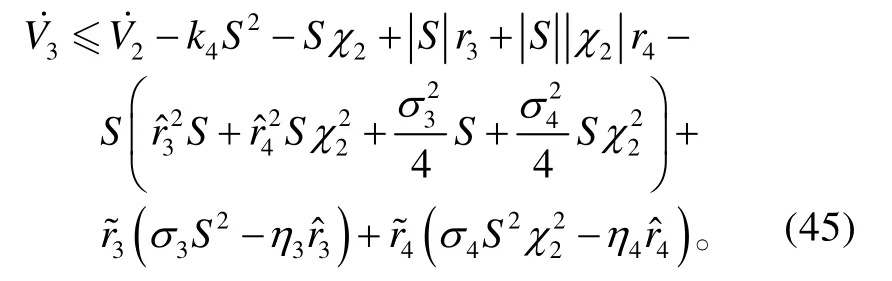
由于

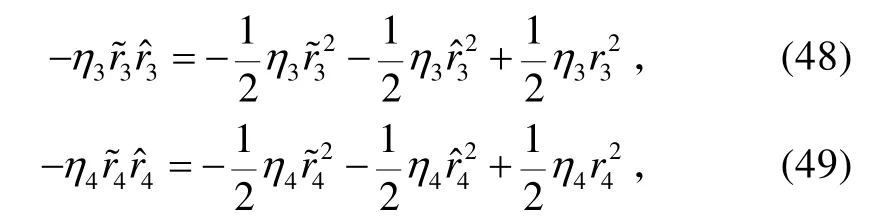
将式(37)、(46)～(49)代入式(45)，可得：

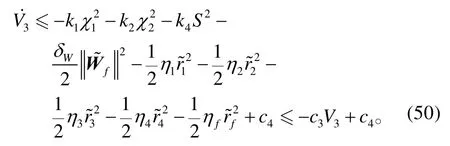
式(50)中：

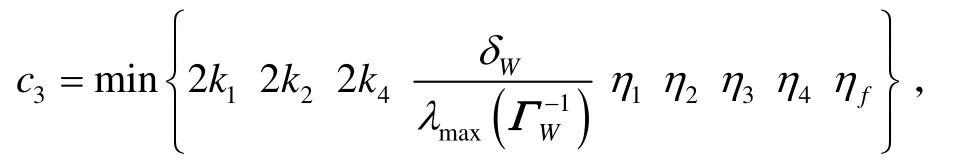
λmax(⋅)表示矩阵“⋅”的最大特征根；

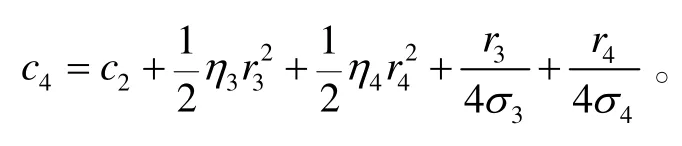
2.3 设计总结

综上所述，可得如下结论。

考虑系统(5)，在假设1的前提下，虚拟控制量和控制量分别采用式(13)、(28)、(39)的形式，模糊逻辑系统的参数调节律采用式(16)的形式，自适应参数和调节律分别采用式(17)、(18)、(32)、(42)、(43)的形式，则系统状态跟踪误差1χ、2χ和3χ，模糊逻辑系统的参数估计误差，以及自适应参数的估计误差均有界且指数收敛至系统原点的一个邻域：

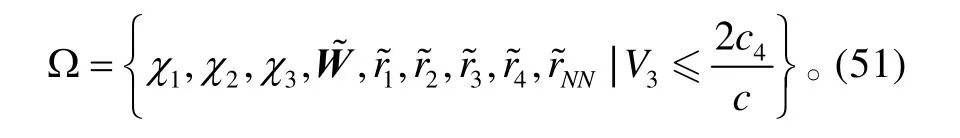
通过式(51)可以看出，调整1k、k2、k4、δW、η1、η2、η3、η4和ηf的值可以调节收敛速度和收敛域的大小。

由于状态变换矩阵T是可逆的，系统(5)与系统(3)属于等价系统，因此，控制量(39)同样适用于系统(3)。

在实际操作过程中，利用弹上的俯仰加速度计可以测量得到ny信号；利用测速陀螺仪可以得到俯仰角速度信号；对于迎角α的获取，可以利用加速度计输出信号 ny与俯仰舵偏角信号δz进行估计，解算公式为将得到的信号矢量经过矩阵T的变换，即可得到控制量(39)中所需的状态向量

3 仿真分析

采用本文提出的控制方法，对反舰导弹的俯仰通道控制回路进行特征点仿真。

俯仰通道动力学模型如式(2)、(3)所示，假设此模型中不确定项分别为：

根据定理1的设计要求，分别选取参数：

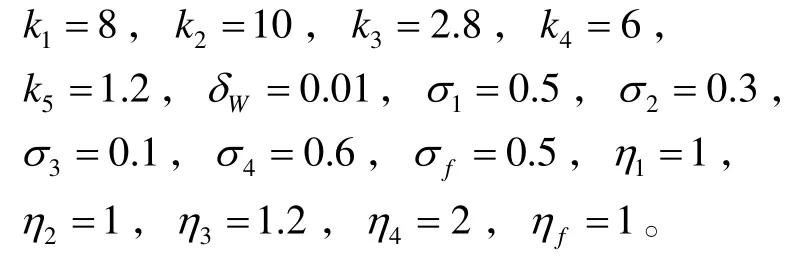
模糊逻辑系统的隶属函数为：

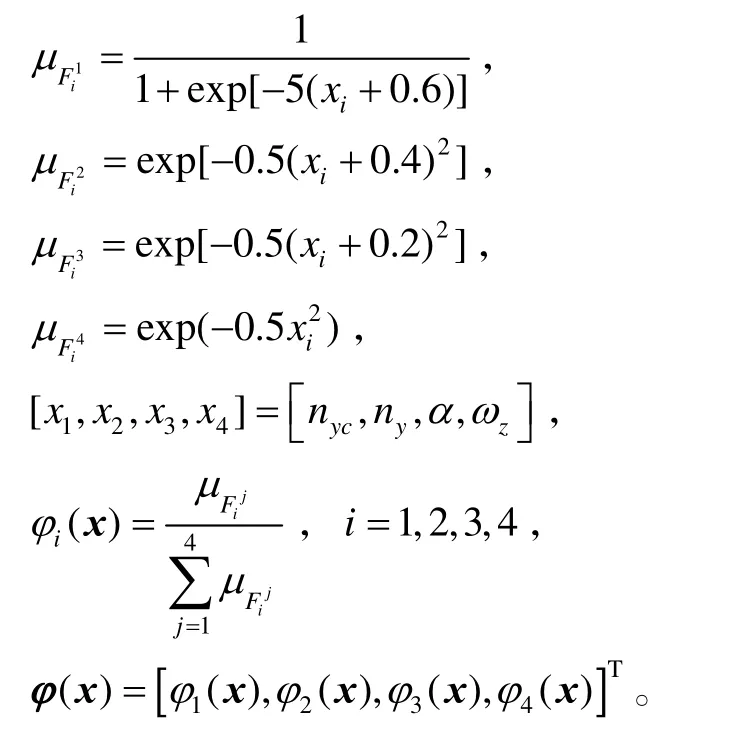
同时，为了削弱滑模控制的抖振现象，对符号函数sgn(S)进行连续化处理，以连续化函数S (|S|+ε)代替sgn(S)，ε=0.003。

运用上述设计的控制器，得到的仿真结果分别如图1～4所示。

在仿真图2中，虚线为法向过载的指令信号nyc，实线为实际法向过载信号 ny。

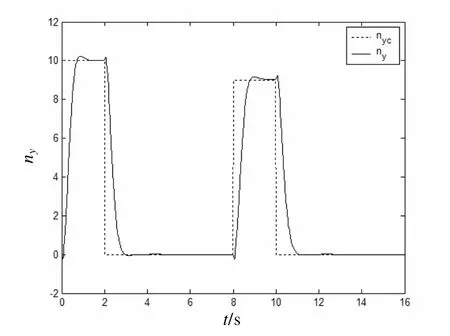
图1 法向过载 ny仿真曲线

图2 迎角α仿真曲线

图3 俯仰角速度ωz仿真曲线

图4 俯仰舵δz仿真曲线

通过此仿真结果可知，当俯仰通道模型存在不确定项时，本文提出的控制方法仍然能够较好地控制 ny、跟踪 nyc，而且迎角α和俯仰角速度ωz信号都在合理范围内，俯仰舵δz没有抖振现象。从而，表明应用本文方法设计的俯仰通道控制系统具有良好的动态品质、跟踪性能和鲁棒性。

4 结论

本文研究了反舰导弹的过载控制系统设计问题，提出了一种自适应模糊滑模控制设计方法。此方法将反演设计、模糊逻辑系统、自适应控制和滑模控制等方法结合起来，利用模糊逻辑系统估计被控系统的虚拟控制量；利用自适应控制方法估计系统不确定项的未知上界；利用反演设计方法进行系统虚拟控制量和实际控制量的推导。基于有限的已知信息，实现对反舰导弹俯仰通道的过载控制，仿真结果表明，所设计的俯仰通道控制系统具有良好的动态品质、跟踪性能和鲁棒性。

[1]崔祜涛.基于自适应神经网络非线性飞行控制[J].航空学报,1998,19(2):173-178.

[2]景韶光.非线性神经网络自适应控制及其在导弹中的应用[J].西北工业大学学报,1997,15(4):603-606.

[3]杨志峰,雷虎民,李庆良,等.基于逆误差补偿的非线性导弹控制器设计[J].飞行力学,2010,28(4):54-58.

[4]杨志峰,雷虎民,李庆良,等.基于RBF神经网络的导弹鲁棒动态逆控制[J].宇航学报,2010,31(10):2295-2301.

[5]于德海,范作娥,史贤俊.带落角约束的末端机动Terminal 滑模导引律设计[J].海军航空工程学院学报,2011,26(5):517-520.

[6]于德海,范作娥,史贤俊.带落角的反舰导弹自适应模糊滑模三维导引律设计[J].四川兵工学报,2011,32(8):52-55.

[7]钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2000:69-70.

[8]任长娥,佟绍成.基于高增益观测器的SISO 非线性系统模糊自适应输出反馈控制[J].辽宁工业大学学报:自然科学版,2011,31(2):71-80.

[9]郭涛,张军英.时滞关联大系统的自适应模糊动态面控制及仿真[J].系统仿真学报,2011,23(2):325-334.

[10]于金鹏,陈兵,于海生,等.基于自适应模糊反步法的永磁同步电机位置跟踪控制[J].控制与决策,2010,25(10):1547-1551.

[11]文杰,姜长生,薛雅丽.严格反馈型非仿射非线性系统的自适应模糊控制[J].控制与决策,2010,25(10):1237-1245.