多传感器组合导航系统的多尺度异步信息融合算法

刘 磊，林雪原，周 旻

（海军航空工程学院 a．研究生管理大队；b．电子信息工程系，山东 烟台 264001）

目前多传感器组合导航系统的信息融合方法已经得到了广泛的研究。而在实际过程中，由于传感器自身性能等条件的约束，各传感器可能具有不同的采样速率，这会使得多传感器信息到达融合中心的时刻不同步，即产生异步问题[1]，目前解决多传感器组合导航系统异步问题的量测方程和状态方程都是建立在单一尺度上的。近年来，多尺度估计理论[2]迅速发展，它吸收了小波变换技术[3]和卡尔曼滤波理论的优点，对信息在不同尺度上进行描述和分析，可以得到更高的滤波精度[4]。

结合多传感器组合导航系统的特点，本文利用数据块分析技术与小波变换技术，建立了一种多尺度异步贯序滤波方法。该方法首先将状态块向量、量测块向量在粗尺度上分解；然后在原始尺度和粗尺度上进行相应的最优卡尔曼滤波，以得到各尺度上平滑信息的最优估计值；最后利用异步贯序滤波方法建立基于全局的最优估计值。论文以SST/GPS/高度表/SINS 组合导航系统为例，对本文算法进行了仿真与验证，结果表明该算法比基于单一尺度的异步滤波算法(简称算法1)具有更高的滤波精度。

1 算法描述

一类在某尺度上建立起来的多传感器单模型动态系统为：

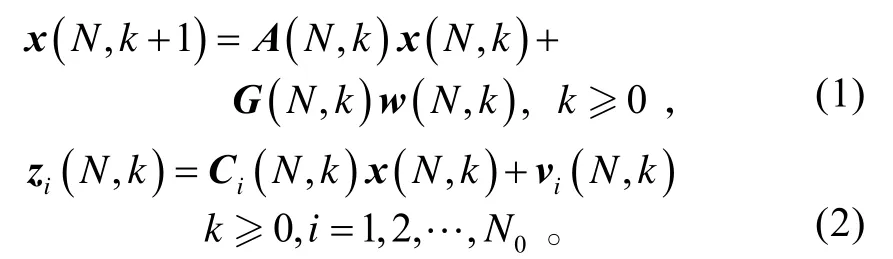
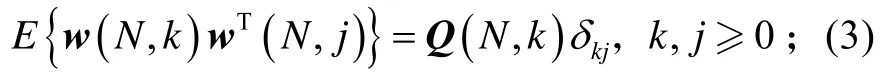
状态初始值x(N,0)为一随机向量，且有：

假设x(N,0)、w(N,k)、vi(N,k)是统计独立的。

将N0个传感器的量测方程(2)组合，得

1.1 系统多尺度描述

多尺度分析的基本思想是用小波变换的方法将

信号分解到不同的尺度上进行分析。分解到粗尺度上的信号称之为平滑信号，而原信号与平滑信号之间的差则称为细节[5]。

若将尺度i上的向量序列写成如下形式的数据块：

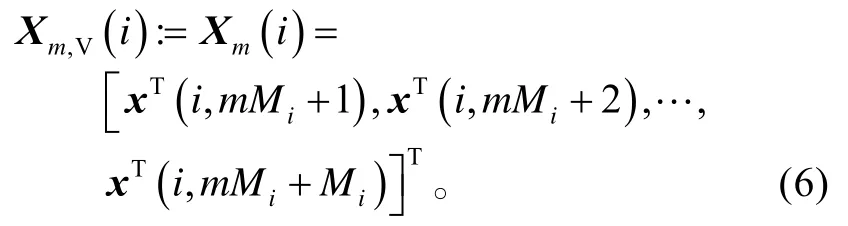
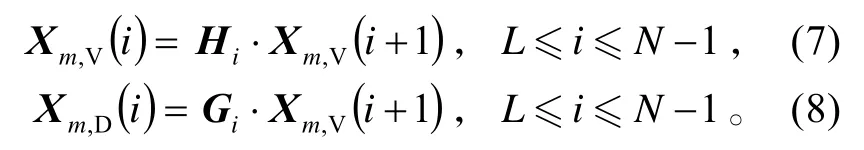
对应的多尺度重构变换为：

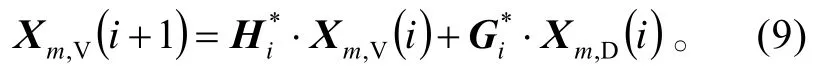
若记

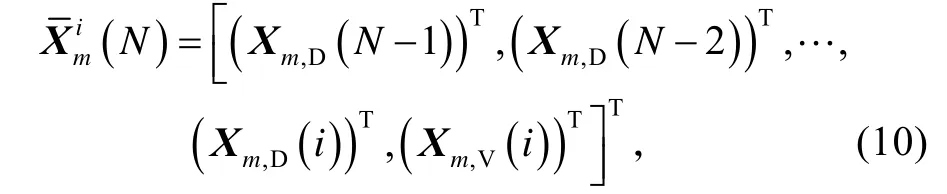
则对应于式(7)、(8)的多尺度分解变换可统一表示为：

而相应的多尺度重构变换式(9)可表示为：

这里，iW是矩阵算子，而且是个正交矩阵，即

1.2 多传感器数据的异步融合算法

对于异步测量系统，传感器的采样率不一致，不能像同采样率情况下对测量值直接进行分块[7]。为了保证每个时刻的状态均有传感器对其观测，不妨假设T1=T0、n1=0成立。

此时对任一时刻k，均有：

如果传感器i在此时有测量值，则相应测量方程为：

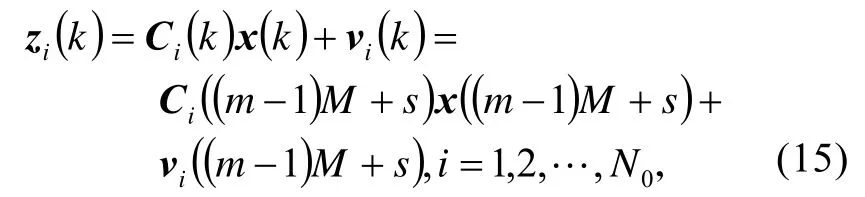
式中，x( (m−1)M+s)是第m个状态块中的第s个元素。记：

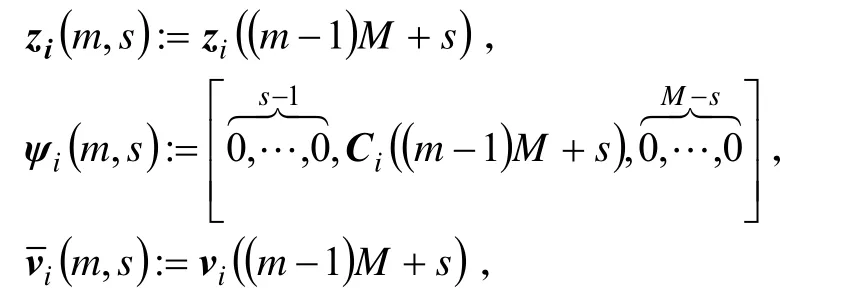
则模型可变为

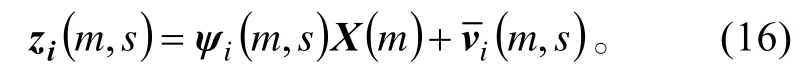
这样就建立了各个传感器在有测量值的时候测量值与整个状态块的关系。利用等式(14)，由模型(16)可得到

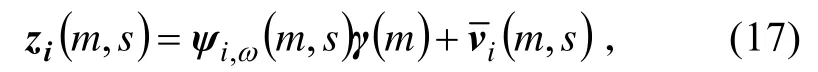
定义mod(ba,)表示数值a对b取模，所得值为a/b的余数。针对异步传感器采样系统，经分析知道，若传感器i在1−k时刻有测量值，那么1−k必是in的整数倍[8]。因此，可以用mod(ink,1−)是否等于零来断定传感器i在k时刻是否有测量值，如下式：

以第m块为例，给出系统的更新过程。

假设1≠m，首先利用第(1−m)块的估计值对当前第m块的状态进行预测，有

时间层面的更新：

对于块内的时刻点s=1, 2,…,M，我们依次用对系统进行更新。

1)当1=s时，传感器层面的更新。

首先，用第一个传感器的测量值z1(m,1)对预测值以及估计误差协方差进行更新，更新方程为：

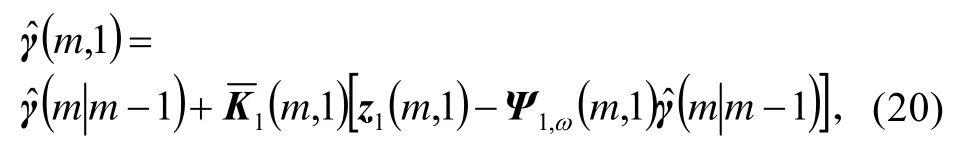
接着，依次检测各传感器，如果有测量值则利用它进行更新。

该时刻的更新结束。

2)当1≠s时。

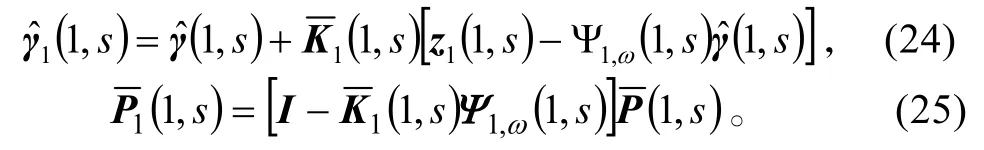
类似1=s的情形，我们用其他传感器在该时刻的测量值以此对进行更新。

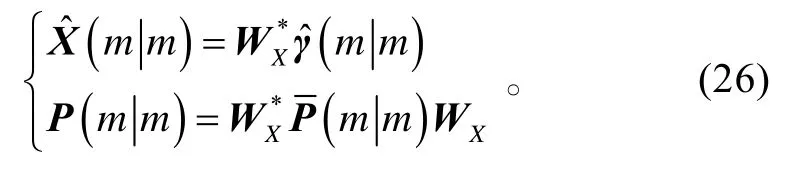
2 仿真实验

本文采用GPS/SST/高度表/SINS 多组合导航系统数学模型，详见文献[10]。仿真系统采用飞行动态仿真和真实导航传感器误差数据生成动态数据的方式。飞行器的初始姿态设为载体水平，航向90º，初始位置(118º，29º，50 m)，滤波器的初始参数主要包括惯性传感器的噪声参数、系统状态的初值和方差阵的初值。依据目前可用的MEMS 惯性传感器的性能指标，给定其方差值，MEMS 陀螺噪声均方根设为0.5 (º)/s，MEMS 加速度计噪声均方根设为10-3g，采样周期为0.02 s；微型GPS 的测速误差0.5 m/s、定位误差8 m(1σ)，SST 姿态误差为200′′；其中GPS、SST、高度表的采样周期分别为1 s、2 s、3 s。实验时，选取的小波为Haar 二进制小波以避免对有限长信号序列进行小波变换时而出现的边界问题[11]；同理对量测量的小波处理也采用Haar 小波。

对相同的SINS、GPS、高度表、SST 仿真数据，本文同时进行了基于本文算法与基于单一尺度的异步滤波算法的滤波实验以比较滤波精度，其中图1～3 分别代表了位置、速度、姿态误差对比曲线。

图1 位置误差曲线比较

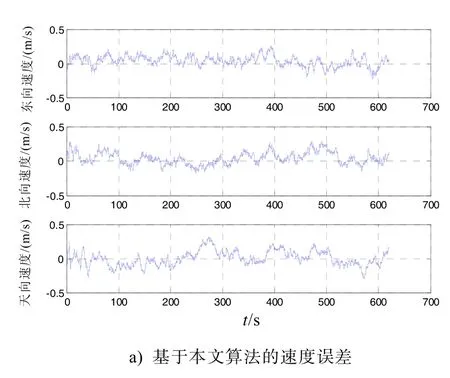
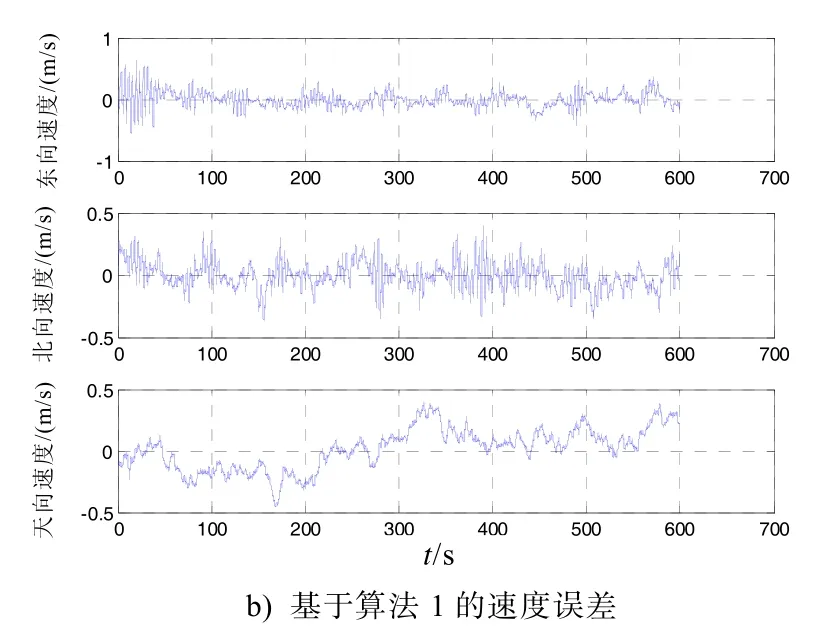
图2 速度误差曲线比较

图3 姿态误差曲线比较

经过对上述实验结果的分析，对于本文算法与算法1，经度误差方差分别为0.811 8 m、2.197 3 m；纬度误差方差分别为1.030 6 m、3.142 7 m；高度误差方差分别为1.941 1 m、7.023 6 m；东向速度误差方差分别为0.006 2 m/s、0.012 4 m/s；北向速度误差方差分别为0.007 9 m/s、0.016 2 m/s；天向速度误差方差分别为0.011 7 m/s、0.019 2 m/s；横滚角误差方差分别为0.002 9º、0.055 1º；俯仰角误差方差分别为0.003 0º、0.037 2º；航向角误差方差分别为0.003 1º、0.853 6º。

从以上实验结果可以看出：本文算法对位置、速度以及姿态的改善是显而易见的。

3 结论

本文算法之所以优于单一尺度的异步滤波算法，是因为本文采用分块估计技术时，块状态内当前状态的估计值在递归地利用其以前各点的观测值进行不断的更新，从而起到了平滑估计的作用。当进一步增加块向量、内向量的个数时，导航参数的误差将会进一步降低，但实时性得不到保证，因而需要综合考虑滤波实时性与滤波精度之间的关系。

[1] 邱爱兵, 文成林, 姜斌. 基于异步多传感器采样量测的最优状态融合估计[J]. 电子学报, 2010,38(7)∶1483- 1485.

[2] YAN L P, LIU B S, ZHOU D H. The modeling and estimation of asynchronous multirate multisenser dynamic systems[J]. Aerospace Science and Technology, 2006,10(1)∶63-71.

[3] 孙延奎. 小波分析及其应用[M]. 北京∶ 机械工业出版社, 2005∶219-224.

[4] 袁信, 俞济祥, 陈哲. 导航系统[M]. 北京∶ 航空工业出版社, 1993∶123-126.

[5] HONG L, CHEN G, CHUI C K. A filter-bank-based Kalman filtering technique for wavelet estimation and decomposition of random signals[J]. IEEE Trans. on Circuits and Systems-II∶ Analog and Digital Signal Processing, 1998,45(2)∶237-241.

[6] 文成林. 多尺度动态建模理论及其应用[M]. 北京∶ 科学出版社, 2008∶181-185.

[7] HONG L. Multi-resolutional distributed filtering[J]. IEEE Trans. on Automatic Control, 1994,39(4)∶853-856.

[8] ZHANG L, WU X, PAN Q, et al. Multiresolution modeling and estimation of multisensory data[J]. IEEE Trans. on Signal Processing, 2004,52(11)∶3170-3182.

[9] 葛泉波, 汪国安, 汤天浩, 等. 基于有理数倍采样的异步数据融合算法研究[J]. 电子学报, 2006,34(3)∶ 543-548.

[10] 林雪原, 衣晓. 一种基于分布式滤波的多传感器组合导航系统算法研究[J]. 武汉大学学报, 2011,36(7)∶ 811-815.

[11] 文成林, 周东华. 多尺度估计理论及其应用[M]. 北京∶ 清华大学出版社, 2002∶221-224.