复合材料后掠翼机翼气动弹性分析

周宏霞，吕锁宁

（1．西北工业大学365 研究所；2．西安爱生技术集团公司飞机室，西安 710065； 3．海军驻西安航空军事代表局，西安 710054）

气动弹性问题伴随着飞机发展的全过程，随着飞机性能的提高，气动弹性问题日益突出，使得气动弹性分析在飞机设计中的作用越来越重要。对于复合材料后掠翼飞机，气动弹性特性是飞机设计需要首先考虑的问题，扭转发散问题一般并不突出，其气动弹性分析应着重考虑操纵面的操纵效率和操纵反效以及颤振临界动压问题。飞机的弹性效应将使弹性状态下的静稳定性导数、操纵性导数、飞行载荷随马赫数和动压的变化与刚体状态存在一定的差别，且在某种情况下变化趋势甚至完全不同。因此，在进行弹性飞机的气弹响应分析时，必须考虑弹性变形对翼面、舵面的气动特性的影响[1-3]。

除了上述气动弹性静力学问题的研究，对于复合材料后掠翼飞机还涉及到气动弹性动力学问题的讨论。在这个领域内，最令人关注的现象就是颤振。颤振或动不稳定性，经常导致结构的灾难性破坏，进行结构颤振分析是非常必要的[4-6]。

本文针对某复合材料后掠翼进行了操纵效率和颤振分析，并详细分析了机翼振动、颤振特性随蒙皮不同铺层比变化的情况。

1 气动力计算与气动弹性求解

气动力计算与气动弹性求解包括：定常气动力计算与静气动弹性特性分析；非定常气动力计算与颤振特性分析[7-10]。

1.1 定常气动力计算与静气动弹性特性分析

1.1.1 亚超声速定常气动力计算

COMPASS 选用计算较方便、效率高的马蹄涡格网法。先将升力面划分为有限个面元，用离散的马蹄涡代替连续分布的涡面(包括尾涡面)。超声速情况下利用一种亚声速马蹄涡方法的推广方法(涡格法)来计算。用“气动力影响系数矩阵”建立升力面局部攻角与气动载荷系数间的关系。

静气弹分析中，使用反映结构节点位移与外载相互关系的柔度矩阵，该柔度矩阵在结构静力分析的基础上形成。

由于气动网格点一般不与结构节点重合，且节点数不等(通常气动网点数少于结构节点数)，必须对原柔度矩阵做合理的凝聚。此外，气动力与升力面斜率分布相关。因此，还需对凝聚后的矩阵作相应转换，由位移分布转换成相应的局部攻角分布。

本系统利用虚功原理，对结构柔度矩阵与气动网格点位移倾角柔度影响系数矩阵，建立二者的变换关系。利用曲面样条插值方法，得到结构点与气动点的转换矩阵。1.1.2 载荷重新分布与发散、操纵效率与操纵反效

气动载荷包括刚性翼面的气动载荷和考虑翼面弹性变形的柔性气动载荷。在弹性变形下，翼面的载荷与刚性情况相比出现了“重分配”。在结构的弹性恢复力与气动力达到自然平衡时，相应的飞行速度为临界飞行速度。当飞行速度超过该值时，气动力矩将大于结构弹性恢复力矩，结构变形会越来越大，很快导致发散破坏。因此，这个临界飞行速度也称为静气动弹性“发散速度”。机翼的发散问题，从物理本质上说，是静稳定性问题，从数学上，作为实特征值问题求解。

在COMPASS 中，考虑的操纵面包括：襟翼、副翼和舵面。操纵面效率指操纵面作单位偏转时，整个柔性翼面(包括操纵面)的气动力或气动力矩与“刚性”翼面时气动力和气动力矩之比。操纵面作单位偏转时的气动力，就是整个翼面的气动力对操纵面偏角的静气动导数；操纵面效率即柔性情况与刚性情况下操纵面偏角静导数之比。本系统可以计算操纵面升力(或侧面力)效率，操纵面纵向力矩效率，操纵面横向力矩效率，以及气动力系数、静气动导数和滚转、俯仰气动导数。

1.2 非定常气动力计算与颤振特性分析

1.2.1 非定常气动力计算

COMPASS 利用偶极子格网法计算亚声速谐振条件下的非定常气动力。该方法可适用于复杂平面形状及机翼/外挂的非定常气动力。这是目前国内外工程上常用的经典方法。采用亚声速空间偶极子格网法进行非定常气动力计算时，须把翼面分为若干布置有振荡压力偶极子的升力面元。它们所引起的下洗使在翼面的控制点上满足边界条件，从而求得翼面的压力分布。

1.2.2 颤振分析与颤振点计算

COMPASS 用v-g法进行颤振分析，该方法也被国内外所广泛采用。此外，还用Laguerre 迭代公式自动确定颤振速度(这一点比NASTRAN 计算要方便得多)。形态插值用曲面样条插值方法进行。

颤振方程的工作形式为

其矩阵形式为

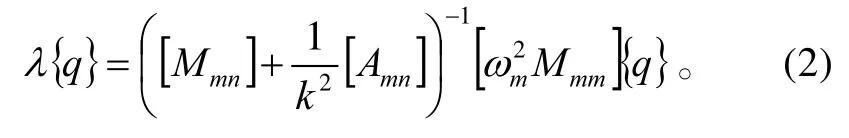
式(2)中：m=1, 2,…,N；[Mmm]为广义质量矩阵；为广义刚度矩阵；ωm为第m阶固有频率；为广义气动力矩阵；k=bω/v为减缩频率，b为平均气动弦长，ω为振动频率，v为颤振速度。

式(2)是一个复特征值问题，可用标准子程序求解复特征值λ及复特征向量{q}。

颤振速度的计算步骤：

1)输入Mmn(m,n=1,2,…,N)、ωm(m=1,2,…,N)，形成矩阵；

2)根据给定的气动外形数据及关于气动分块的要求，求得有关几何数据；

3)输入自振型{fm}(m=1, 2,…,N)，可取自振动计算或试验结果。用其计算气动小块所需点的值，以求解广义气动力；

4)给定ρ及M值；

5)给定若干缩减频率值kl(l=1,2,…,L)，对每一个kl值，求出广义气动力矩阵[Amn]，求解复特征值问题，得N组解

6)按相同n序号的L组解，作v-g图及v-ω图。通常在v-g图上，取g=0 的v值为颤振速度，记作vFg=0。相应可在v-ω图上确定ωFg=0。

本系统采用Laguerre 迭代公式确定颤振速度。这为含有颤振约束的优化设计带来极大方便。

2 计算模型

本文所采用的计算模型为某高速后掠翼无人机，机翼为双梁式结构，带一个后缘操纵面。主翼面蒙皮、梁为对称均衡铺层的复合材料层合板，肋为金属材料，操纵面为蜂窝结构。蒙皮、腹板采用复合材料板壳元；梁凸缘、肋缘条采用当量杆元；舵面和主翼面采用多点约束。依据机翼结构的对称性及载荷对称性可得边界：机翼与机身连接处的节点有节点位移δx=0、δy=0、δz=0。整个模型共230 个节点，675 个单元，4 个气动分区，80 个气动小块。机翼结构有限元模型见图1。

图1 有限元模型

3 计算结果

3.1 操纵效率计算结果

静弹分析的定常气动边界条件为：主翼面偏角为0，副翼偏角为1 个单位。海平面不同马赫数下的对称气动力下副翼操纵效率分别为柔性、刚性翼面气动力，计算结果见表1。

表1 海平面下副翼操纵效率

3.2 颤振计算结果

为分析不同高度下颤振速度随马赫数变化的情况，根据颤振计算要求，对4 组种高度/马赫数的组合状态进行分析。图2 为0 m、2 000 m、4 000 m、7 000 m 高度下，颤振速度随马赫数变化曲线。H=0，Ma=0.76 的颤振v-g图和v-f分别见图3、图4。

图2 初始参数时不同高度下颤振速度随马赫数变化曲线

图3 颤振v-g 图

图4 颤振v-f 图

从图2 中可以看出，在0 m、2 000 m、4 000 m、7 000 m 高度下，并不是在所有颤振设计点处颤振计算值都能大于颤振设计值。

从图3、图4 中看出复合材料的弯扭耦合效应都相当突出，均为第四支(即一扭)最先发散，发生二弯和一扭的颤振耦合。

颤振速度受升力面弯曲刚度和扭转刚度的影响，为了改进结构设计，详细分析了机翼振动、颤振特性随蒙皮不同铺层比变化情况，具体结果见表2。

表2 变化不同铺层比对机翼振动、颤振特性影响

针对以上分析情况，调整复合材料蒙皮0°、90°、±45°铺层比例，分别由最初的25%、25%、50%调整到现在的40%、20%、40%，并将蒙皮厚度由初始的1 mm，调整到1.25 mm。调整铺层比后不同高度下颤振速度随马赫数变化曲线见图5。从图5 中可以看出，在所有颤振设计点处颤振速度均满足设计要求。

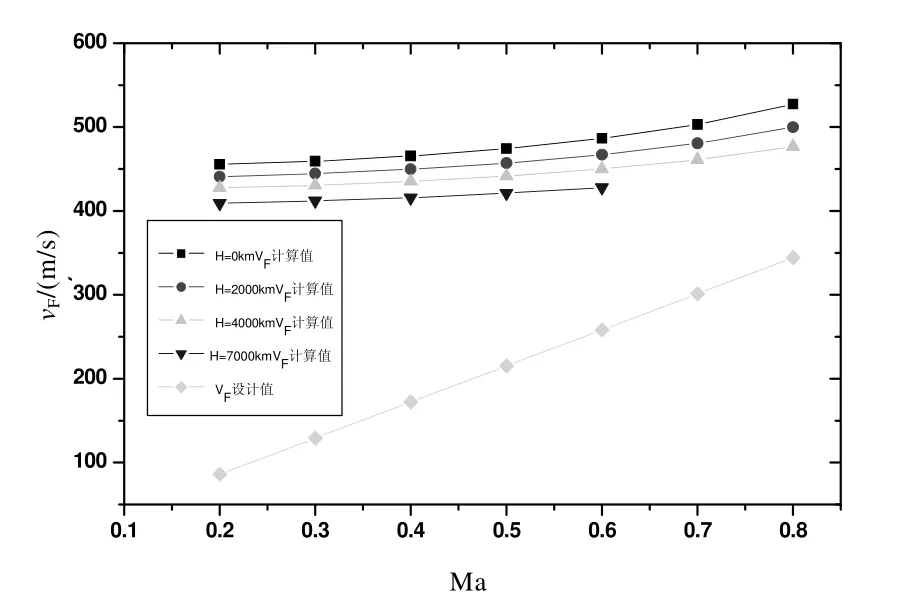
图5 调整铺层比后不同高度下 颤振速度随马赫数变化曲线

4 结论

1)在海平面(即H=0 km)，舵面操纵效率随着马赫数的增加而降低。这主要是因为操纵效率是随着飞行动压、副翼反效动压与扭转发散动压之比而变化的，而后掠机翼的扭转发散动压往往大于副翼反效动压，当飞行动压越接近反效动压，操纵效率越趋于0。这说明，飞机设计一方面要尽可能提高副翼反效动压和扭转发散动压；另一方面还要通过设计参数调整选择合适的副翼反效动压与扭转发散动压之比，使飞行范围内的操纵效率尽可能高。

2)在飞行范围内，最初的结构设计不能满足颤振要求；通过对比分析机翼振动、颤振特性随蒙皮不同铺层比变化情况，发现调整0°、±45°和90°铺层比例，可以提高结构扭转刚度，从而提高飞机颤振发散速度。显然，为了满足后掠翼对于发散、颤振等要求，使用复合材料剪裁技术是非常必要的。

[1] 杨超, 许赟, 解长川. 高超声速飞行器气动弹性力学研究综述[J]. 航空学报, 2010,31(1):1-11.

[2] 张华, 马东力, 马铁林. 弹性变形对柔性机翼气动特性影响分析[J]. 北京航空航天大学学报, 2008,34(5): 487-490.

[3] 李珂. 大展弦比飞翼布局飞机气动弹性特性研究[D]. 西安: 西北工业大学, 2007.

[4] 葛鹏. 大展弦比机翼的颤振分析[D]. 天津: 天津大学, 2010.

[5] 肖志鹏, 万志强, 杨超,等. 复合材料机翼鲁棒气动弹性优化设计[J]. 复合材料学报, 2010,27(2):127-132.

[6] 万志强, 杨超. 大展弦比复合材料机翼气动弹性优化[J]. 复合材料学报, 2005,22(3):145-149.

[7] 张伟伟, 叶正寅. 基于CFD 的气动力建模及其在气动弹性中的应用[J]. 力学进展, 2008,38(1):77-86.

[8] 杨国伟. 计算气动弹性若干研究进展[J]. 力学进展, 2009,39(4):406-420.

[9] 陈桂彬, 邹从青, 杨超. 气动弹性设计基础[M]. 北京: 北京航空航天大学出版社, 2004:64-74.

[10] 管德. 非定常空气动力计算[M]. 北京: 北京航空航天大学出版社, 1991:100-141.