基于Bayesian-MCMC方法的水体污染识别反问题*
2012-03-19陈海洋滕彦国王金生宋柳霆周振瑶
陈海洋,滕彦国,王金生,宋柳霆,周振瑶
(北京师范大学水科学研究院,北京 100875)
随着我国经济的快速发展,各种自然灾害和人们的生产经营活动带来的环境风险不断加剧,突发性水体污染事件时有发生,给人民群众的生命健康、财产安全和生态环境造成了巨大损失.迅速找出污染源位置、掌握其排放强度、了解事件发生的初始时间,对于开展污染应急处置具有重要的现实意义.然而事件发生时,这些信息往往是不确知的,也是不适定的.为此,需根据水体环境系统的自身特点,构建污染扩散对流控制方程,利用已有水文水质参数以及浓度场的部分信息,推求污染源位置、源强及事件发生初始时间,即为环境水力学反问题.
与已知水力水质参数推算污染物浓度的正问题不同,反问题通常会由于测量数据有限且带有噪声,使得污染源识别成为不适定问题[1].常见的反演方法有正则化方法[2]、优化算法[3]、数值法[4]和统计反演法[5]等.其中建立在贝叶斯统计学基础上的贝叶斯推理能以概率语言来描述和解决工程反问题,可以较好地用来实现污染源识别反问题的求解[6].
当前,环境水力学反问题研究尚处于起步阶段,研究成果不多,且以参数反演居多,部分源项识别研究以数学方法证明为主,对模型边界条件、初始条件假设过于严格[7].本文基于贝叶斯推理和二维水质扩散对流模型,考虑有限宽度河流的瞬时岸边污染泄漏,建立水体污染识别数学模型,以典型Metropolis算法构建马尔科夫链,取得污染泄漏源源强、泄漏位置和污染泄漏初始时间3个模型参数后验概率分布,并通过基于混合遗传模式搜索算法的求解结果进行比较,分析MCMC-Bayes方法的识别效果.
1 正问题
一个考虑二维水质对流扩散方程可以表述为:
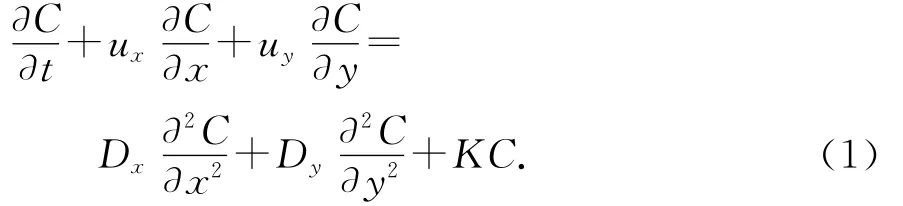
式中:C为(x,y,t)处的污染物质量浓度,mg/L;ux和uy分别为河流纵向和横向的流速分量,m/s;Dx和Dy分别为河流纵向和横向的混合系数,m2/s;K为污染物降解系数,d-1.
对于瞬时点源排放,方程解析解可表示为:

式中:h为河流深度;M为污染物排放量,g/s;B为点源到边界的距离,m;其他同上.如在岸边排放,则B=0,有:
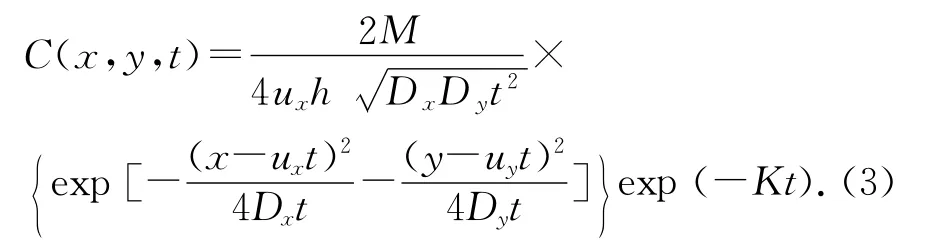
2 基于MCMC-Bayes方法的污染识别反问题
2.1 贝叶斯推理
贝叶斯推理基于如下贝叶斯公式:
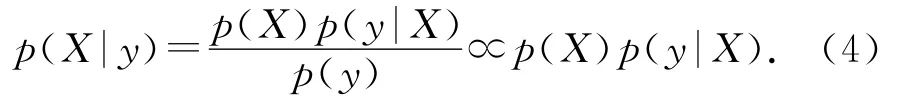
式中:p(X|y)为参数的后验概率密度函数;X为模型参数;y为观测数据;p(X)为参数的先验概率密度函数;p(y|X)为条件概率密度;p(y)为积分常数.
通常,环境水力学的模型参数都分布在一个特定的范围内,满足独立的均匀分布,其先验概率密度函数可定义为:

则总的先验分布可表示为:

而污染物浓度场的测量噪声一般可以认为是白噪声,其误差服从均值为零、标准偏差为σ的正态分布,ε~N(0,σ2),条件概率密度定义为:

式中:n为测量数据个数.
把式(6)~(7)代入式(4),并把分母表示的常数项正规化为1可得:

理论上,利用式(8)可以获得任何环境模型参量的统计矩,但事实上,后验概率密度的求解算法较为复杂,难以得出明确的解析表达式.另一方面,随未知参量维数的增加,数值积分算法的计算量将呈指数增长,实现复杂而难度较大.为此,需要采取其他改进的方法以实现后验概率密度的求解.
2.2 马尔科夫链蒙特卡罗法
马尔科夫链蒙特卡罗法(Markov Chain Monte Carlo,简称MCMC)是近期发展起来、可很好地用来求解贝叶斯后验概率密度的统计方法.其基本思想是对定义在高维随机向量空间的无明确数学表达式的概率分布p进行抽样,产生大量服从分布p的随机向量序列,通过建立合适的抽样算法使得该序列满足马尔科夫链性质,以保证向量Vi+1的产生仅依赖于向量Vi,而与Vi-1,Vi-2,…,V1等向量无关.这样,抽样算法完全可以由转移概率矩阵P来描述,矩阵元素pij表示当前访问向量Vj的条件下接着将要访问Vi的条件概率[8].
可见,MCMC方法利用Markov链机制探索状态空间以生成样本的方法能够保证Markov链花更多的时间在最重要的区域,产生的样本更能够模仿目标分布样本.常见的构造Markov链转移概率矩阵的方法有Gibbs抽样算法、Metropolis-Hastings算法、Metropolis算法和自适应Metropolis算法等.本研究采用Metropolis算法.
2.3 Metropolis算法
Metropolis是Metropolis-Hastings算法的特例,其Proposal分布函数满足对称随机游走,即q(X*|X(i))=q(X(i)|X*).从当前位置X(i)获得候选抽样值X*,Markov链从X(i)位置移动到X*的接受概率为[9]:
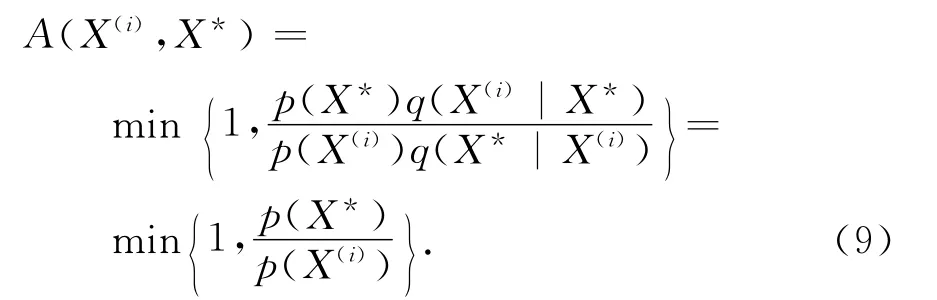
式中:p(X*),p(X(i))为目标概率密度函数,在贝叶斯推理中为条件概率密度.
2.4 基于Metropolis算法的反演思路
1)在模型参数先验范围内随机产生模型参数初始点X(i)(i=1);
2)利用水质模型计算出模型参数初始点对应的污染物浓度值,并计算出该模型参数对应的条件概率密度L_MODEL;
3)根据Proposal分布在当前参数X(i)状态下提取新的测试参数X(*),利用水质模型计算出测试参数X(*)对应的污染物浓度及条件概率密度L_TEST;
4)产生一个0~1之间的随机数u,如果u<min(1,L_TEST/L_MODEL),则接受该测试参数并设定为当前模型参数,即X(i+1)=X(*),否则不接受该测试参数,X(i+1)=X(i);
5)重复步骤3),4)直至达到迭代次数.
3 实例与讨论
模拟案例假定如下:某河段断面A上游发现污染带前锋,经检测污染物为B危险化学品,现需利用断面A带噪声的浓度场部分分布数据反演上游污染泄漏源位置、初始泄漏时间及泄漏强度.假定该河流河段均匀,河流水文条件稳定,河段断面积、平均流速稳定,满足二维水质模型应用条件,污染排放为岸边瞬时泄漏,相关参数及先验信息见表1;A断面污染物浓度监测数据见图1;初始监测时间为发现污染带后的第一时间,某日下午15时,后每隔30 min监测一次,直至当日下午19时.

表1 某河流断面水文水质参数Tab.1 Model parameters of study area

图1 断面A污染物观测浓度序列Fig.1 Simulation observe concentration serial of site A
3.1 反演分析
假定污染物从岸边瞬间排入河道,泄漏量为M,泄漏地点距离A断面S0,泄漏时间距离首次监测时间为T0,参数“真值”见表1.利用表1中的3个模型参数真值及其他参数计算出断面A的污染物浓度分布,初始监测时间为发现污染带后的第一时间,某日下午15时,后每隔30min监测一次,直至当日下午19时,见图1.
从图1可以看出,9组A断面污染物浓度序列近似正态分布,最高值发生于该日16时30分,污染物质量浓度达到1.62mg/L,到19时已经降低为0.19 mg/L.据先验信息,该突发污染事故可能为交通事故导致的污染物泄漏或化学品企业储罐爆炸泄漏瞬间排入河流造成的污染.
设坐标中心为污染源泄漏点,测点A坐标为(S0,0),待反演参数定义为X(M,S0,T0).根据先验信息,3个待反演模型参数先验分布为均匀分布,其对应的先验概率密度函数分别为:
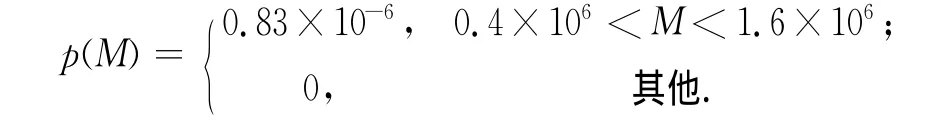
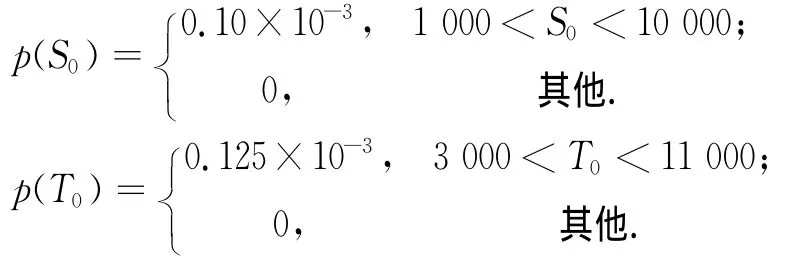
假定观测误差为白噪声N(0,σ2),σ=0.01,条件概率密度表示为:
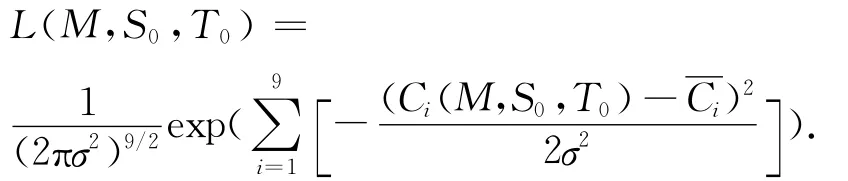
根据贝叶斯定理,模型参数的后验概率密度函数为:

式中:λ为一比例常数.
3.2 反演结果
取Proposal分布为均匀分布q(X*|X(i))=U(X(i)-ΔX,X(i)+ΔX),步长为先验范围的5%,取ΔX(M,S0,T0)=(60 000,450,400),按照Metropolis算法反演思路迭代10 000次.3个参数的迭代曲线见图2,参数后验概率直方图见图3.

图2 参数反演迭代曲线Fig.2 Iteration curve of model parameters
从图2可看出,迭代约2 000次后,M,S0,T0均达到稳定,马尔科夫链进入稳定收敛区域.从图3可看出,3个模型参数后验概率密度呈现不太明显的正态分布;污染源源强M在1 000 000g附近的频度最大,完全符合预定设定初值;污染源距离A断面距离S0在5 000m附近的频度最大,与预先设定值完全符合;而污染泄漏时间距A断面首次监测时间T0在7 000~8 000s区间频度最大,与预先设定值较为接近.

图3 参数后验概率直方图Fig.3 Posterior histogram of model parameters
3.3 反演效果分析
为进一步验证反演结果,剔除前面2 000次结果,对其他8 000次模型参数进行后验统计分析,分析结果见表2.可以看出,3个参数的数学期望误差、中值误差均较小,而以污染源强度M的误差最小.
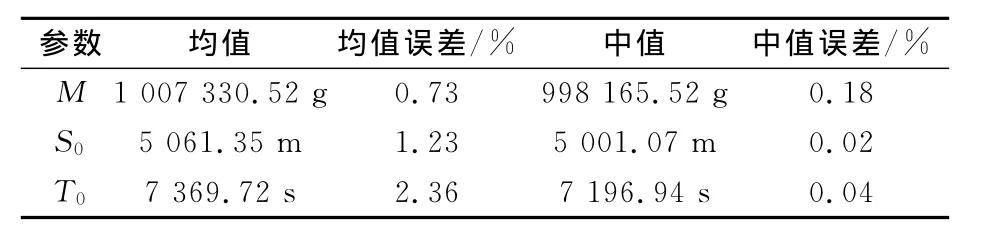
表2 污染源参数后验统计结果Tab.2 Posterior statistical results of model parameters
为了检查基于MCMC-Bayes方法的反演稳定性,采取多次间隔性反演提取模型参数反演误差序列,见图4.可以看出,反演结果较稳定,3个参数的相对误差均在9%以内,平均误差分别为2.94%,2.50%和2.21%.比较而言,污染源源强M的误差起伏较大,位于[0.48%,8.48%];污染源位置S0的误差起伏次之,位于[2.50%,5.90%];污染源泄漏时间T0的误差起伏最小,位于[2.21%,4.65%].

图4 基于MCMC-Bayes问题反演误差分析Fig.4 Error serial with method of MCMC-Bayes
作为比较,本文采用混合遗传模式搜索算法对该问题进行求解,反演误差见图5.可以看出,采用混合遗传模式搜索算法求解的问题解误差较大,最高误差达到24.7%,3个参数的平均误差分别达到3.20%,4.08%,7.45%.其中污染源泄漏时间T0的误差起伏最大,位于[1.21%,24.7%];污染源源强M的误差起伏次之,位于[0.54%,10.69%];污染源位置S0的误差起伏最小,位于[0.68%,13.33%].

图5基于混合遗传模式搜索算法的问题反演误差分析Fig.5 Error serial with method of hybrid GA-Patter search
两种方法反演的模型参数误差比较见表3.很明显,基于MCMC-Bayes的源识别误差远小于优化算法,3个参数的最小误差、最大误差和平均误差都呈现明显的特征,可见,相对优化算法而言,基于MCMC-Bayes的源识别方法具有良好的可靠性和稳定性.

表3 基于MCMC-Bayes 和混合遗传模式搜索算法(GA-PS)的反演误差对照Tab.3 Error comparison with method of MCMC-Bayes and GA-PS%
4 结 论
污染源识别对于开展突发污染事故应急处置、加强水质管理和控制具有重要的现实意义,而由于测量数据有限且带有噪声等原因使得污染源识别成为一个不适定问题.本研究基于贝叶斯推理和二维水质模型建立水体污染识别数学模型,运用马尔科夫链蒙特卡罗法抽样获得了污染源源强、污染源位置和污染泄漏时间3个模型参数的后验概率分布和统计结果.实例研究结果表明,基于马尔科夫链蒙特卡罗抽样算法的贝叶斯推理可以较好地用来实现水体污染识别,具有识别精度高、误差小的特点,其可靠性和稳定性高于混合遗传模式搜索优化算法.
总体看来,MCMC-Bayes通过构造Markov链进行随机动态模拟,实现对高维空间无明确数学表达式概率分布密度函数的数值计算,且具备计算速度快、复杂度不依赖于计算空间维数等特点.同时,它可以方便地将各种先验信息和误差信息高效地融合到问题求解过程中,减小问题的不确定性,获得全局最可能解,可以很好地用来开展同属问题不适定的水体污染反问题研究.
[1] 戴会超,王玲玲.工程水力学反问题研究及应用[J].四川大学学报:工程科学版,2006,38(1):15-19.DAI Hui-chao,WANG Ling-ling.Study and application of the inverse problem on hydraulics[J].Journal of Sichuan University:Engineering Science Edition,2006,38(1):15-19.(In Chinese)
[2] 刘继军.不适定问题的正则化方法及应用[M].北京:科学出版社,2005:42-46.LIU Ji-jun.Regularization methods of ill-posed problems and its application[M].Beijing:Science Press,2005:42-46.(In Chinese)
[3] 闵涛,周孝德,张世梅,等.对流扩散方程源项识别反问题的遗传算法[J].水动力学研究与进展,A辑,2004,19(4):520-524.MIN Tao,ZHOU Xiao-de,ZHANG Shi-mei,et al.Genetic algorithm to an inverse problem of source term identification for convection-diffusion equation[J].Journal of Hydrodynamic Ser A,2004,19(4):520-524.(In Chinese)
[4] 王泽文,邱淑芳.一类流域点污染源识别的稳定性与数值模拟[J].水动力学研究与进展,A辑,2008,23(4):364-371.WANG Ze-wen,QIU Shu-fang.Stability and numerical simulation of pollution point source identification in a watershed[J].Journal of Hydrodynamic Ser A,2008,23(4):364-371.(In Chinese)
[5] 严齐斌.河流水质参数估计的蒙特卡罗方法[J].水利水电技术,2006,37(10):14-16.YAN Qi-bin.Monte Carlo method for estimation on parameters of river water quality[J].Water Resources and Hydropower Engineering,2006,37(10):14-16.(In Chinese)
[6] 朱嵩,刘国华,毛根海,等.利用贝叶斯推理估计二维含源对流扩散方程参数[J].四川大学学报:工程科学版,2008,40(2):38-43.ZHU Song,LIU Guo-hua,MAO Geng-hai,et al.Application of Bayesian inference to estimate the parameters in 2Dconvection-diffusion equation with source[J].Journal of Sichuan University:Engineering Science Edition,2008,40(2):38-43.(In Chinese)
[7] 刘晓东,姚琪,薛红琴,等.环境水力学反问题研究进展[J].水科学进展,2009,20(6):885-890.LIU Xiao-dong,YAO Qi,XUE Hong-qin,et al.Advance in inverse problems of environmental hydraulics[J].Advance in Water Science,2009,20(6):885-890.(In Chinese)
[8] 曹小群,宋君强,张卫民,等.对流扩散方程源项识别反问题的MCMC方法[J].水动力学研究与进展,A辑,2010,25(2):129-135.CAO Xiao-qun,SONG Jun-qiang,ZHANG Wei-min,et al.MCMC method on an inverse problem of source term identification for convection-diffusion equation[J].Journal of Hydrodynamic Ser A,2010,25(2):129-135.(In Chinese)
[9] ANDRIEU C,FREITAS N D,DOUCET A,et al.An introduction to MCMC for machine learning[J].Machine Learning,2003,50:5-43.
