加性白噪声下基带延迟锁定环跟踪精度的计算

余金峰,杨文革,路伟涛,孟生云

(1.装备学院, 北京101416;2.中国洛阳电子装备试验中心,河南 洛阳471003)

1 引 言

在扩频测量系统和卫星导航系统中,接收机完成了信号的捕获之后,就转入对接收信号的跟踪。本地参考信号对接收信号的跟踪包括载波和扩频码序列跟踪两部分。载波的跟踪采用锁相环技术(PLL),扩频码序列的同步跟踪通常采用延时锁定环路(DLL)。DLL 与PLL 在技术原理上是一致的,都是通过反馈环路来实现输出信号对输入信号的跟踪与同步,其差异在于产生误差信号的相位鉴别器不同。在PLL 中,环路的误差信号是由鉴相器或乘法器产生的,而在DLL 中,环路的误差信号是由延迟锁定鉴别器产生的。

在测量和导航设备中,测距功能的实现是以扩频码的跟踪为基础的。在噪声环境下,噪声与输入信号一同进入同步跟踪环,使得环路输出信号也受到噪声的影响,使跟踪信号产生跟踪抖动,从而影响测距性能。因此,码跟踪环在高斯白噪声下的跟踪精度是测控和导航系统中的一个重要问题。文献[1-4]中都对这一问题进行了研究。

文献[1]在对码鉴相器建模时,对输入信号和噪声采取了不同的处理方法,输入信号与本地信号进行相关运算,也就是相乘并积分的过程,而对噪声则仅考虑了相乘运算,绕过了积分过程。这样处理的结果是使得鉴相器输出端的噪声仍然是白噪声,该白色噪声特性与积分时间无关。此噪声经环路滤波后在输出端产生噪声,也就使得给出的跟踪精度公式与环路带宽有关,而与积分时间无关。

文献[2]中则考虑了积分过程对噪声的作用,没有把噪声当白色噪声处理,但其没有对噪声进行全面分析,仅给出了噪声的方差,该方差与积分时间有关。同时,文献[3]中还以鉴相器等效输入噪声特性代替环路输出端等效噪声特性作为环路跟踪精度,忽略了环路对等效输入噪声的作用,这实际上是降低了环路对噪声的抑制作用。所以,其给出的精度公式与积分时间有关,而与环路带宽无关。

本文在已有研究的基础上,系统研究了码跟踪环在加性白噪声下的跟踪精度问题。在码鉴相器中,将输入信号与输入噪声作同样的相关处理,得到了等效输入噪声相关特性和功率谱密度,并考虑跟踪环路对噪声的作用,最终得到了跟踪环路输出信号的跟踪精度,使得两种不同的结论得到了统一。

2 码延迟鉴别器的等效线性模型

在系统稳定工作的情况下,接收机载波环能够提供相干载波。因此,在分析码跟踪精度时,可以忽略载波的作用,采用基带模型。数据信号D(t)在延迟锁定环中的作用是影响相关积分结果的极性,使得一直为正的相关积分结果随着数据位极性的变化而改变。但通过对积分结果的处理,可以消除数据位极性的影响,只是积分时间的选择应避免跨越数据位的跳变。因此,本文不考虑数据位的影响。

基带相关延迟锁定环由延迟鉴别器、回路滤波器、压控振荡器和码产生器等组成,其结构如图1 所示。图1 中,延迟锁定环把接收信号与超前码和滞后码进行相关处理,相关处理的结果相当于在相关函数峰的上升沿和下降沿分别进行采样。两个采样信号的差值是本地码和输入码之间延迟差的非线性函数。对采样信号通常采用称为零搜索的控制方式,也就是说,零搜索方式控制本地码的延迟,使得超前相关器与滞后相关器输出信号差别趋零。超前和滞后相关器之间的固定时间间隔称为相关器间距,通常用码元Tc为单位来表示, dTc表示相应的时间间距。

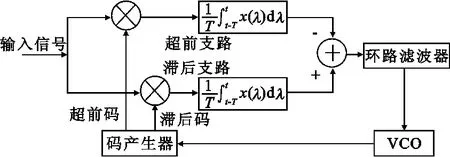
图1 码延迟锁定环结构图Fig.1 The structure diagram of DLL

设输入信号r(t)为输入码和噪声之和:

式中, Cx(t-τ)为输入码信号分量, n(t)为输入基带噪声分量。本节讨论信号分量。

超前和滞后支路的输出信号SE和SL为

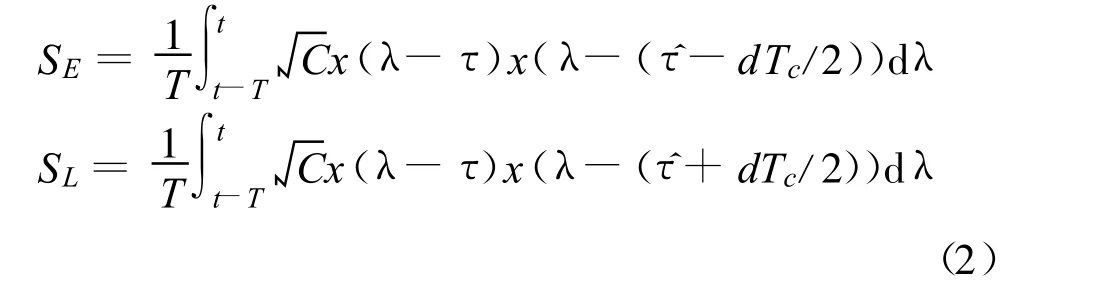
记Δτ=τ- τ,上式用相关函数表示为

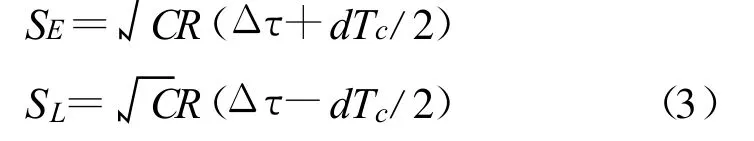
鉴别函数通过将滞后采样减去超前采样得到:

鉴别函数如图2 所示,图中所示为d=1 时的情形,其图形简称为S 曲线。其中间部分呈现线性特性,靠近原点处的斜率为

图2 码延迟锁定环鉴别函数(d=1)Fig.2 The function of discriminator in DLL when d=1

因此,对于码延迟差Δτ=(τ- τ)来说,等效鉴相器增益为k′d=2 C/Tc。鉴相器等效框图如图3(a)所示。鉴相器输出信号vd为

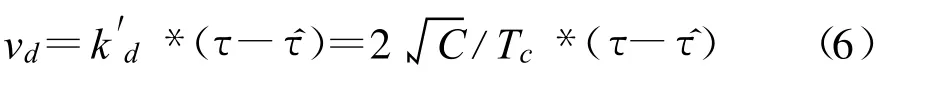
图3 码延迟锁定环鉴相器等效框图Fig.3 Equal effects of the discriminator in DLL

对于经码元时间Tc 相位化后的码延迟相位差Δτ/Tc=(τ- τ)/Tc 来说,等效鉴相器增益为kd =2 C。相应的鉴相器等效框图如图3(b)所示。鉴相器输出信号vd为

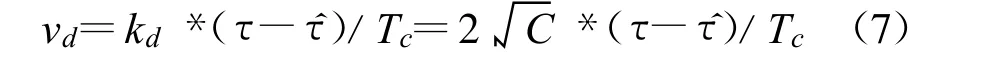
式(6)与式(7)的输出信号相等。

3 同步跟踪回路输入噪声的等效处理

本节讨论在码延迟鉴相器输入输出端的噪声分量。假设输入噪声是均值为零、功率谱密度为N0/2的白噪声。

设噪声在超前与滞后支路的输出信号分别为

两个支路的差值Nd(t)为

Nd(t)的均值为零,相关函数为

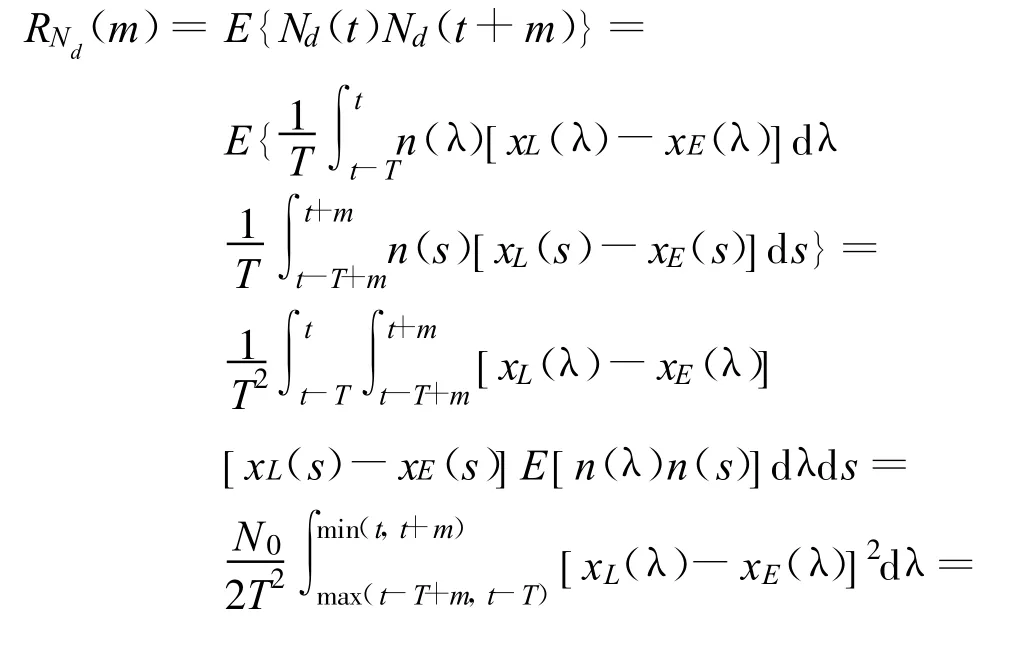
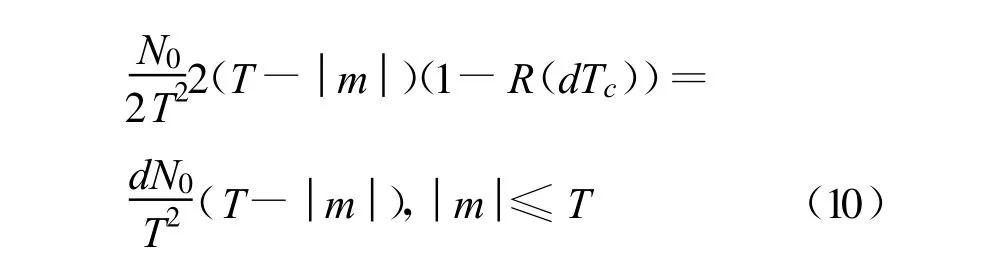
对上式求傅里叶变换,得Nd(t)的功率谱密度:

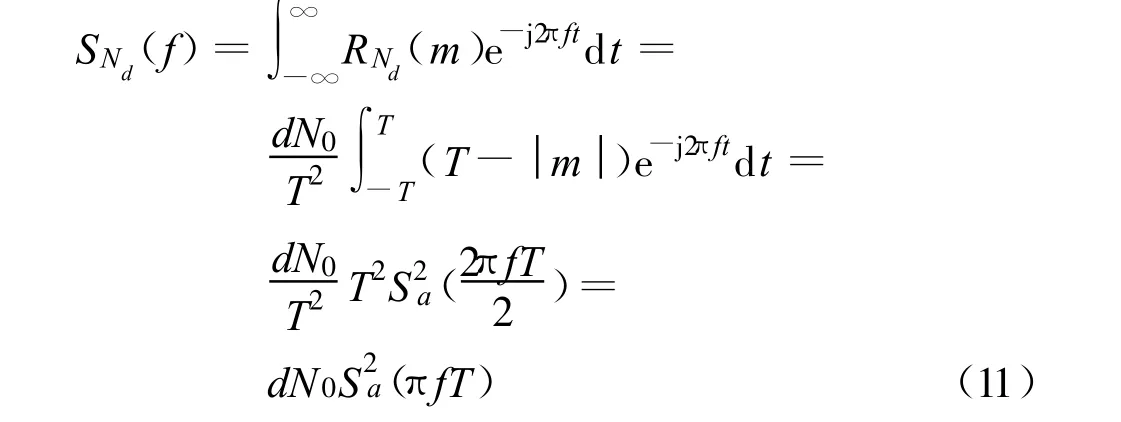
因此,鉴相器输出端的Nd(t)是均值为零、功率谱密度为SNd(f)的噪声。Nd(t)的相关函数和功率谱密度如图4 所示。

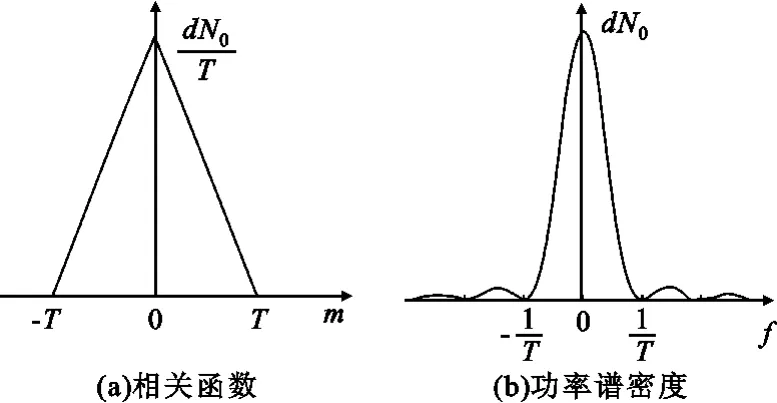
图4 鉴相器输出端噪声的相关函数和功率谱密度Fig.4 The correlation function and PSD of the noise in discriminator

如前所述,码延迟鉴相器的等效增益kd=2 C,Nd(t)在鉴相器输入端的等效输入可记为Nτ/Tc:

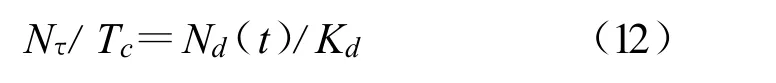
则Nτ/Tc均值为零,功率谱密度为

由上述讨论可知,输入噪声经码延迟鉴相器处理之后,相当于在等效线性鉴相器输入端码延迟相位信号τ/Tc上附加了一个均值为零、功率谱密度由式(13)表示的非白噪声Nτ/Tc。

4 码延迟锁定环等效线性相位模型

设回路滤波器传输函数为F(f), 冲激响应为h(t)。回路滤波器的输出v(t)是鉴相器输出vd(t)与h(t)的卷积积分:

滤波器的输出信号v(t)送往VCO 作为控制信号,通过控制振荡器的振荡频率来调整本地码的时延,使本地码延迟与输入码延迟的差值趋零。

根据VCO 输出信号与控制电压的关系,可以写出以下的相位关系等式:

式中, f0是VCO 静态工作频率, k0是VCO 的控制灵敏度。

整理上式,并以积分算子p 代替积分号,可得:

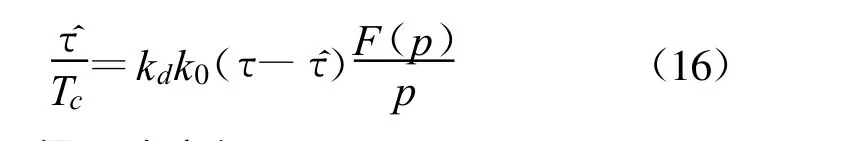
由上式可得回路方程:

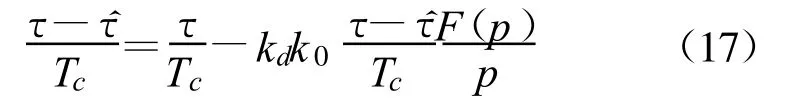
由回路方程可给出码跟踪环的等效相位模型图,如图5 所示。

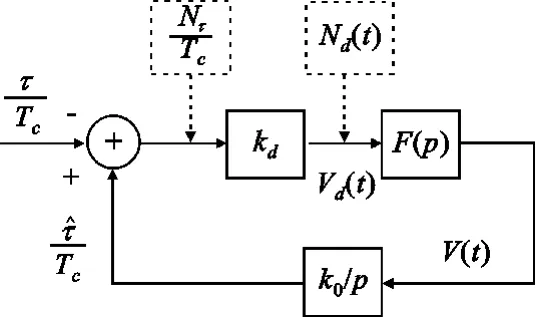
图5 码延迟锁定环等效线性相位模型Fig.5 The equivalent linear phase model of DLL

回路闭环传递函数HL(s)为

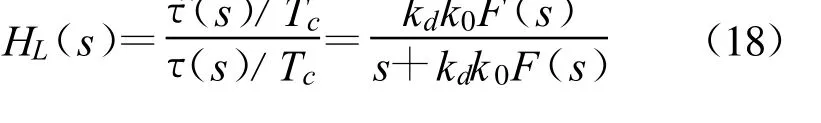
5 加性白噪声下码跟踪精度计算

在第3 节中已经说明,鉴相器输出的噪声分量Nd,在鉴相器等效增益为kd的情况下,可以等效为鉴相器输入端的等效码延迟噪声Nτ/Tc,其等效模型如图5 中虚线框中所示。

利用环路闭环传输函数H(j2πf)和输入相位噪声功率谱密度SNτ/Tc(f),可求得输出相位噪声功率谱密度SNτ/Tc(f)为

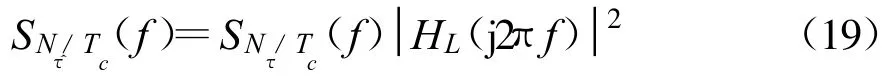
环路输出端等效相位噪声方差为

对上式的计算,根据积分带宽(1/T)与环路带宽BL的关系,可以采用两种简化方法:第一种是当环路带宽远小于积分带宽时,环路带宽对输出相位噪声起主要作用,简化积分带宽的作用;第二种是当积分带宽远小于环路带宽时,积分带宽对输出相位噪声起主要作用,简化环路带宽的作用。

第一种情况下,环路带宽远小于积分带宽,可以用输入噪声零频率处的谱密度来近似计算输出噪声的谱密度:

从而,整个环路的码延迟跟踪精度为

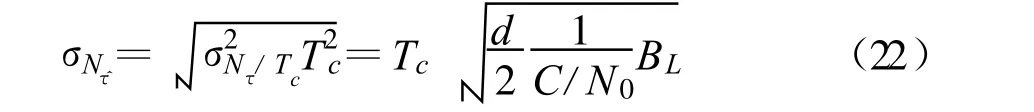
第二种情况下,积分带宽远小于环路带宽,可以用传递函数零频率处的值来近似计算输出噪声的谱密度:

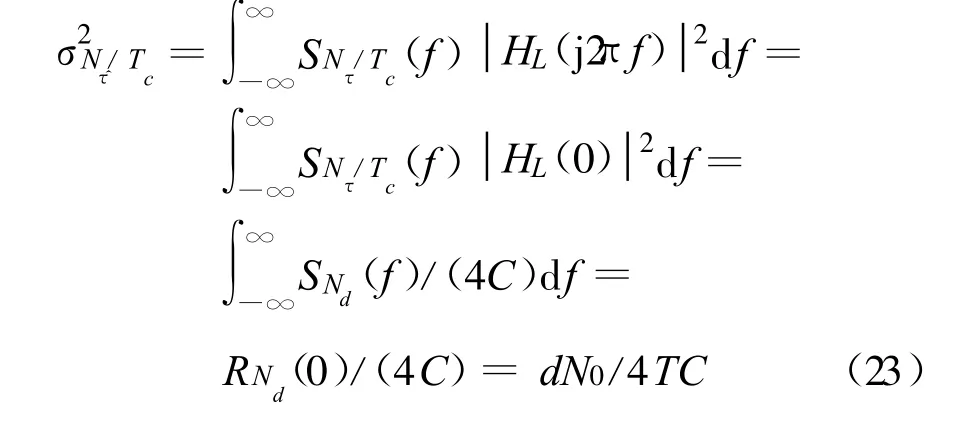
从而,整个环路的码延迟跟踪精度为

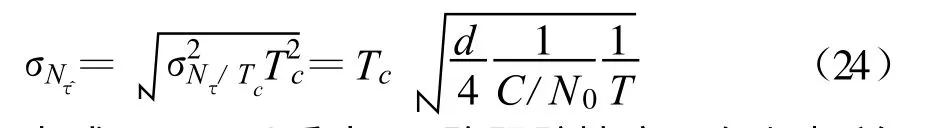
由式(20)可以看出,环路跟踪精度不仅与相关器间距d、码元宽度Tc 和信噪比C/N0有关,还与积分时间T 和环路闭环传递函数HL(j2πf)有关。在对式(20)进行简化处理后,可以得到式(22)和(24)。在式(22)和(24)中,d 、Tc和C/N0是一样的,不同的是两式中分别有参数T 和BL,并且1/T 和2BL具有相同的位置。对两个公式的选择,取决于积分时间T和环路带宽BL 的相对关系,选用数值小者进行计算,因为它对噪声的滤波起主要作用。同时,在设计跟踪环路时,也可以根据情况灵活选择参数,对一个参数提高要求时,对另一个参数就可以适当放宽要求。

6 有关结论的比较与分析

文献[1]中,在对鉴相器建模时,对码信号和噪声采取了不同的处理方法。考虑了积分器对信号的作用,而忽略了积分器对噪声的作用,这样的处理使得输出端仍然是白色噪声,实际上是忽略了积分器对噪声的过滤作用。而由本文前述内容可以看出,输入端白噪声经积分器作用后,在输出端不再是白色噪声,而是功率谱有效宽度与积分时间T 有关的有色噪声,其相关函数成三角形,功率谱密度成S2a(x)形。

同样在文献[1]中,对环路输出端噪声的处理是以相位抖动的方式给出的,没有给出以码延迟抖动形式表示的跟踪精度。本文给出了以跟踪环输出端噪声标准差作为跟踪精度的计算方法,更为直接,更为合理。对文献[1]中给出的公式作进一步的推导,可以得到与式(22)相同的表达式。因此,可以认为,文献[1]中的结论符合本文讨论的第一种情况,适合于环路带宽较小、对输出相位噪声起主要作用的情况。

文献[2]中则是以输入端的码延迟抖动标准差作为跟踪精度,忽略了跟踪环路对噪声的过滤作用,其给出的计算公式与式(24)相同。所以,文献[2]中的结论符合本文讨论的第二种情况,适合于积分带宽较小、对输出相位噪声起主要作用的情况。

综上所述,可以认为,本文的讨论综合了文献[1]和文献[2]中两个相矛盾的结论,分析了两个结论的适用情况,是对两者的统一。

7 结束语

本文在已有研究的基础上探讨了加性白噪声下基带码延迟跟踪环跟踪精度的计算问题。以基带码延迟鉴别器的等效相位模型为基础,研究了在线性鉴别器特性下输入加性噪声的等效模型,得到了鉴相器输出端有色噪声的相关函数和功率谱密度公式;推导了以跟踪环输出端噪声标准差作为跟踪精度的计算方法;在积分时间和环路带宽分别起主导作用的情况下,得到了跟踪精度的两种简化计算方法,两种简化方法的结果分别与有关文献的结果相一致,使两种不同的结论得到了统一。文中给出的结果是以有关研究为基础的,并进行了一定的改进和拓展,所得结果要更为合理和全面。

[ 1] Peterson R L, Ziemer R E, Borth D E.扩频通信导论[M] .侯永宏,马兰, 译.北京:电子工业出版社,2006:81-85.

Peterson R L, Ziemer R E, Borth D E.Introduction to Spread Spectrum Communications[M] .Translated by HOU Yonghong,MA Lan.Beijing:Publishing House of Electronics Industry, 2006:81-85.(in Chinese)

[ 2] Misra P, Enge P.全球定位系统-信号、测量与性能[M] .罗鸣,曹冲, 肖雄兵, 等, 译.北京:电子工业出版社,2008:323-330.

Misra P,Enge P.Global Positioning System Signals,Measurements,and Performance[M] .Translated by LUO Ming,CAO Chong,XIAO Xiong-bing, et al.Beijing:Publishing House of Electronics Industry,2008:323-330.(in Chinese)

[3] 沈允春.扩谱技术[M] .北京:国防工业出版社, 1995:178-186.

SHEN Yun-chun.Spread spectrum technology[M] .Beijing:National Defense Industry Press,1995:178-186.(in Chinese)〗

[4] 田日才.扩频通信[M] .北京:清华大学出版社, 2007:208-214.

TIAN Ri-cai.Spread spectrum communication[M] .Beijing:Tsinghua University Press,2007:208-214.(in Chinese)

[5] 陈世伟.锁相环路原理及应用[M] .北京:兵器工业出版社,1990:102-105.

CHEN Shi-wei.The principle and application of phase -locked loop[M] .Beijing:Arms Industry Press, 1990:102 -105.(in Chinese)

[6] 张厥盛, 郑继禹, 万心平.锁相技术[M] .西安:西安电子科技大学出版社,1994:63-65.

ZHANG Jue-sheng,ZHENG Ji-yu,WAN Xin-ping.Phase-lock technique[M] .Xi′an:Xidian University Press, 1994:63-65.(in Chinese)