自组装耦合量子点中的类氢杂质

张红，熊红彦，谷洪彬

(1.河北工程大学理学院，河北邯郸056038;2.盘锦职业技术学院，辽宁盘锦124010)

自上个世纪80年代以来，低维半导体材料中杂质态的各种性质就引起了人们的广泛关注［1-4］。杂质对于材料中的电子输运及光学性质有重要影响，杂质态结合能与激子结合能有着定性上的一致。Li Shushen［5-6］在有效质量近似下采用包络函数的方法分别对分级自组装 GaAs/ AlxGa1-xAs量子点和立方体量子点中的电子态以及杂质结合能进行了计算，研究了外加电场对杂质能级和结合能的影响。Perez-Merchancano S T［7］研究了球形量子点中杂质态的流体静压力效应。以上研究集中在对单量子点中杂质态性质进行的讨论，关于耦合量子点中杂质态性质的研究尚不多见。Wang Xue-feng［8］采用变分的方法对双量子点中类氢杂质的结合能进行了计算，讨论了量子点间距对结合能的影响。Liu Jian-jun［9］采用变分的方法计算了流体静压力对杂质态结合能的影响。Xia Congxin［10］基于有效质量近似对外电场作用下闪锌矿结构的GaN/AlGaN耦合量子点中类氢杂质的基态能进行了研究。

目前，尚未看到关于磁场对耦合量子点中杂质态性质影响的讨论，关于耦合量子点的结构参数对量子点中杂质结合能影响的研究也不够系统。基于此，本文在有效质量近似下采用差分计算的方法，系统研究耦合量子点中类氢杂质结合能随量子点的结构参数、杂质位置和束缚势的变化规律，进而讨论外加磁场对此的影响。

1 理论框架

量子点结构横向(x、y方向)采用抛物形量子势，纵向(z方向)采用高斯势，两个量子点沿z方向并行排列，外加磁场沿z轴方向。以杂质态波尔半径ad=h2e/e2作为长度单位，Rydberg常数Rd=e2/2εad作为能量单位，在此单位制下杂质的哈密顿可以表示为

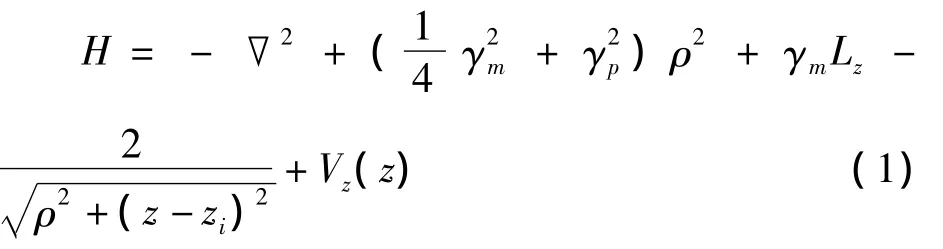
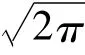
采用差分法对式(2)进行计算，得到最小本征值ED，ED为杂质态的基态能。

杂质的基态结合能Eb=Ee-ED，式中Ee-电子基态能。图1给出了沿z方向量子点的示意图。

2 讨论与分析

本文将以GaAs耦合量子点为例进行讨论。高斯势V0=200 meV，介电常数e=12.5，电子有效质量=0.067m0，相应的波尔半径ad=9.87 nm，Rydberg常数Rd=5.83 meV。

图2给出的是杂质位于其中一个量子点中心、横向束缚势分别为γ=0.3和γ=2、势垒宽t= 5 nm、10 nm和20 nm时，类氢杂质结合能随着量子点尺寸的变化情况。从图2(a)中可以看出，在垒宽为10 nm和20 nm时，杂质结合能随着量子尺寸的增大先增大后减小。这是因为在量子点尺寸较小时，波函数将会穿过势阱在边界势垒层分布，从而影响杂质中心对电子的束缚;随着量子点尺寸的增大，电子隧穿的几率减小，相应的结合能将会增加;然而当量子点尺寸进一步增大时，量子隧穿将逐渐退居次要地位，电子波函数将主要集中在一个量子点中，由于量子限制效应，结合能将会随着量子点尺寸的增大而减小。在垒宽为5 nm时与其它两个垒宽较大的情况不同，杂质结合能随着量子点尺寸的增大先减小后增大，在小于5 nm的尺寸时有一个最小值;当增大到最大值的时候又开始减小。出现这种现象的原因在于势垒的宽度极小，量子点间耦合较强，电子波函数主要集中在量子点空间范围，量子点限制效应占主导地位，随着量子点尺寸的增加杂质的结合能减小，隧穿和量子空间限制达到一个平衡时结合能达到最小值，之后的变化趋势就同势垒较宽时的相同了。另外，极大值出现的位置会随着势垒的减小而向右移动，这主要是由于量子空间限制效应引起的。从图2(b)中可以看到，将量子点置于强度为10 T的磁场中，杂质的结合能将明显增加，并且横向束缚较小的量子点中杂质的结合能受到磁场的影响更为明显。势垒为5 nm的量子点中杂质结合能的变化曲线同其它两种垒宽的情形一致，不再有最小值。这是由于磁场的影响，增强了杂质中心对电子束缚造成的。

图3给出的是杂质位于量子点中心横向束缚势γ=0.3和γ=2的耦合量子点中，量子点尺寸分别为2 nm、5 nm和10 nm时杂质结合能随着量子点间势垒宽度变化的情况。不同量子点尺寸的变化曲线各不相同。量子点尺寸Z=2 nm垒宽较小时，量子点间的耦合较强，波函数主要分布在量子点空间，相对扩散到边界势垒的波函数较小，因此结合能较大;随着垒宽的增加，波函数空间分布变大，结合能变小;当波函数空间分布和势垒隧穿达到一个平衡时，结合能达到最小值。之后，随着耦合作用减小，波函数的空间分布逐渐集中在一个量子点中，杂质的结合能随着量子点间势垒增大逐渐增强，并最终达到一个稳定值。这时，两个量子点间耦合作用降到最低，可以看作是两个独立的单量子点。量子点尺寸为5 nm时，随着垒宽的增加没有结合能减小的情况，与量子点尺寸为10 nm的情形相比，在垒宽较小时杂质的结合能增加得不明显。也就是说，随着量子点尺寸的增大杂质结合能随势垒变化曲线的极小值将向左移动，当量子点尺寸为5 nm和10 nm时，量子点的尺寸足够大，向边界势垒扩散的波函数不再明显，也就不出现结合能减小的情况了。图3(b)与图3 (a)相比，可以明显看到磁场增强了杂质中心对电子的束缚，跟图2呈现的结果是一致的。

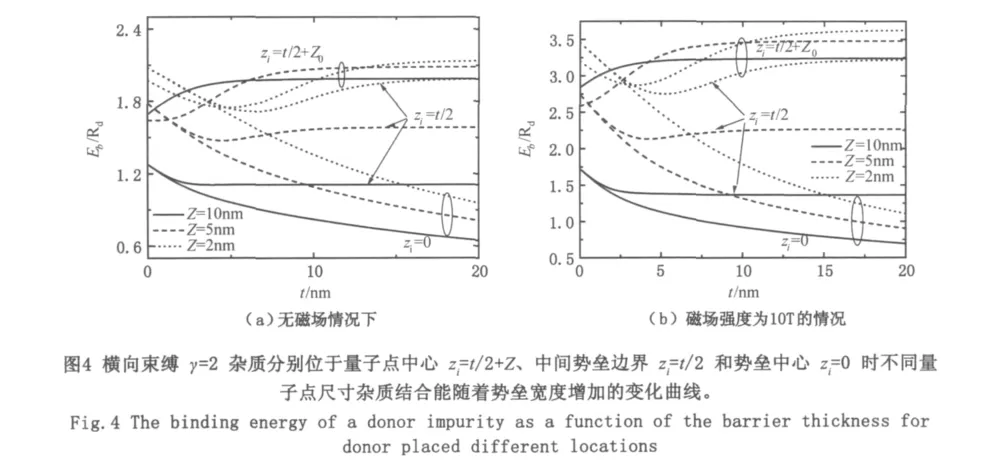
图4给出了杂质处于不同位置时杂质结合能随着势垒宽度的变化情况。关于杂质位于量子点中心的情况在图3中已经讨论过，这里我们只对位于中间势垒边界和中间势垒中心的情况进行讨论。杂质位于中间势垒边界，量子点的尺寸在2nm和5nm时，杂质的结合能先减小后增大，然后趋于常量，特别是量子点尺寸为2nm时更为明显。这在图3的讨论中已经讨论过，由于耦合作用较强，波函数在量子点空间分布较集中结合能较大，随着势垒的增加，耦合作用的结果使得波函数的空间分布范围增加，引起结合能的减小，量子空间限制和电子向边界势垒的隧穿达到一个平衡时有极小值出现;随着势垒的进一步增大，耦合减小，结合能增大，直到耦合作用消失，结合能达到单量子点时的大小，成为常量。与杂质位于量子点中心时相比，由于在中间势垒的边界，波函数在势垒中的分布增加使得杂质的结合能较小。杂质位于中间势垒中心时，不论量子点尺寸如何，杂质的结合能都将随着势垒的增加而单调减小。这是因为杂质位于势垒的中心，而电子则分布在量子点空间，势垒越厚，杂质中心对电子的束缚越弱。图4 (b)和图4(a)相比可以看到，磁场对杂质位于中心时杂质结合能的影响要明显大于其它两种情况，而杂质位于中间势垒中心时受到磁场的影响最小。并且，杂质处于相同位置在相同量子点尺寸时，磁场对势垒宽度较小的杂质结合能影响要大于对势垒较宽时的影响。

3 结论

1)中间垒宽较大时，位于量子点中心的杂质其结合能随着量子点尺寸的增加先增加后减小;在垒宽较小时，首先有个变小的过程。

2)量子点尺寸较小的量子点，位于量子点中心的杂质其结合能随着势垒的增加先减小后增加;当量子点尺寸较大时，不再有减小的过程。

3)随着杂质位置的变化，杂质结合能也会发生变化，杂质处于量子点中心时杂质结合能最大。

4)磁场有明显增强杂质结合能的作用，并且当杂质位于量子点中心时，对约束势较弱的杂质其影响越强;对于杂质处于不同位置而言，磁场对位于量子点中心的杂质结合能影响最强，对位于中间势垒中心的杂质结合能影响最弱。

［1］QU F Y.Intense field effects on hydrogen impurities in quantum dots［J］.J Appl Phys，1997，82:1236.

［2］GRANADOS D.In(Ga)As self-assembled quantum ring formation by molecular beam epitaxy［J］.Appl Phys Lett，2003，82:2401.

［3］AN X T.Hydrogenic impurities in parabolic quantumwell wires in a magnetic field［J］.Appl Phys，2006，99:123713.

［4］ZHANG M.Pressure influence on the Stark effect of impurity states in a strained wurtzite GaN/AlxGa1-xN heterojunction［J］.Chin Phys:B，2009，18(10):4449 -4455.

［5］LI S S.Electronic structure and binding energy of a hydrogenic impurity in a hierarchically self-assembled GaAs/AlxGa1-xAs quantum dot［J］.J Appl Phys，2006，100:083714.

［6］LI S S.Binding energy of a hydrogenic donor impurity in a rectangular parallelepiped-shaped quantum dot: Quantum confinement and Stark effects［J］.Appl Phys，2007，101:093716.

［7］PEREZ-MERCHANCANO S T.Hydrostatic-pressure effects on the donor binding energy in GaAs-(Ga，Al) As quantum dots［J］.Phys:Condens Matter，2007，19: 026225.

［8］WANG X F.Hydrogenic impurity in double quantum dots［J］.Phys Lett A，2007，364:66-69.

［9］LIU J J.The influence of compressive stress on shallowdonor impurity states in symmetric GaAs-Ga1-xAlxAs double quantum dots［J］. Appl Phys， 2007，101:073703.

［10］XIA C X.Electron and impurity states in GaN/AlGaN coupled quantum dots:Effects of electric field and hydrostatic pressure ［J］. Appl Phys， 2010，108:054307.

［11］SZAFRAN B.Parity symmetry and energy spectrum of excitons in coupled self-assembled quantum dots［J］. Phys Rev B，2001，64:125301.