一种基于非均匀马尔可夫随机场的图像分割方法

张 辉，胡阳涟

（1．咸阳师范学院 数学与信息科学学院，陕西 咸阳 712000；2．西安理工大学 理学院，陕西 西安 710054）

在图像处理和计算机视觉领域，图像分割是其中的一个难点，也是重点。它的目的是将我们感兴趣的目标从图像复杂的背景中提取出来，以便进行更深入的分析和处理。图像分割方法多种多样，如基于阈值的分割方法，基于边缘的分割方法，基于内容的分割方法，基于统计的分割方法等。基于马尔可夫随机场（MRF）模型的图像分割方法[1]，是一种基于统计的分割方法，以其模型参数少，空间约束能力强，易于和其他方法相结合等优点，在图像分割以及其他图像分析领域中得到了广泛的应用。

基于MRF模型的图像分割是基于贝叶斯后验概率理论的。一般采用双MRF，一个随机场对应于观测图像，另一个随机场对应于未知的分类标号，通过迭代算法将图像的局部信息逐步传递到整个图像，以求得分割标号的最大后验概率（MAP）。传统的基于 MRF模型的图像分割都是基于均匀MRF随机场的，即假定MRF中的耦合系数是一个常数。然而，在许多图像中，不同的纹理特征有不同的耦合系数，假定一个耦合系数会带来分割效果的明显变差，且不具有自适应性。近年来，许多学者提出了基于非均匀MRF的图像分割[2]，将图像建模为一个非均匀的MRF，改善了分割效果。非均匀MRF与均匀MRF的不同之处在于非均匀MRF采用的是可变的耦合系数，而均匀MRF的耦合系数是一个常数。一般将图像分为大小相等的子块，再用期望最大化（EM）算法[3]估计每个子块中心象素点的耦合系数，利用线性插值，得到每个象素点的耦合系数。由于子块的划分没有利用任何统计信息和边缘信息以及相邻像素之间的相互影响，因此这种估计方法并不准确。本文提出在图像预分割的基础上，结合图像的统计性质和边缘信息对图像进行四叉树分解，把图像分成不同大小的子块。再根据每个子块的大小以及子块内边缘信息的丰富程度，估计出非均匀MRF的耦合系数。实验表明，本文的估计方法较为准确，将它应用到图像分割中，能增强图像分割的自适应性，改善分割效果。

1 基于非均匀MRF的图像分割

图像分割问题实际上可以看作是图像的标记问题。平面上的象素点集为 S，满足 S={s1，s2，ΛΛ，sM×N}，图像象素点的总数为M×N。假定得到观测的图像数据为F，ω为图像的标记场，ω=（ωs1，ωs2ΛΛ，ωsM×N），ωs∈Λ={1，2，ΛΛ，L-1}，L 是类别的总数。图像分割问题转化为求解标记场ω，使得Bayes后验概率达到最大。

其中P（ω）是标记场ω的先验概率，是关于图像结构一般性知识的概率描述；P（F|ω）是观察值F的条件概率分布（也称为似然函数）。P（F）是观测场的概率。因为观测数据F是给定的，所以P（F）是一个常量。因此有：

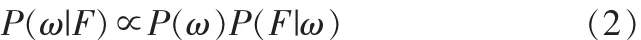
因此只要定义出先验概率P（ω）和似然函数P（F|ω）就可以把图像分割问题转化为如下的最优化问题：

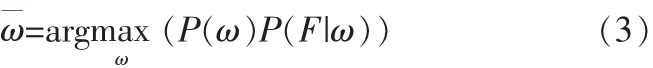
根据大数定理，假设概率P（F|ω）服从高斯分布，且类别λ用它的均值μλ和方差σλ来表示，则似然能量函数可以表示如下：

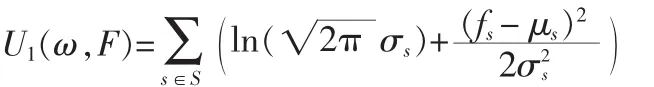
对于先验模型，假设它符合MRF模型。由Hammersley-Clifford定理[4]可知，一个马尔可夫随机场与一个 Gibbs随机场等价。因此只要定义了Gibbs随机场的能量函数[5]，那么这个MRF也就确定了。Gibbs随机场的概率密度函数可以表示为：

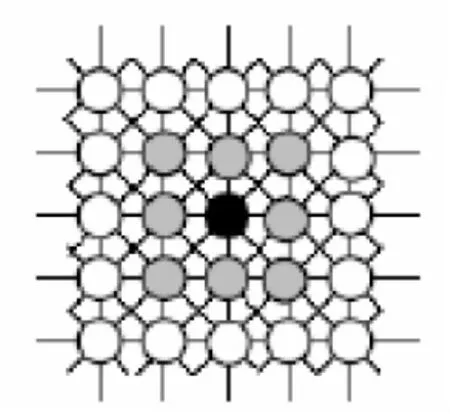
图1 8-邻域系统Fig．1 Eight-Neighborhood

因此势团势能计算公式可以表示为

相应的先验能量函数为

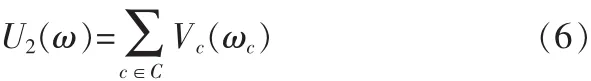
其中 βs即为像素点 S的耦合系数， 通常在区间[0．1，2．4]上取值，它控制区域的同构性，在均匀MRF中，βs是一个常数。在非均匀MRF中，βs是需要根据图像特征去估计的一个变数，这也是均匀MRF和非均匀MRF的不同之处。下面将介绍一种估计耦合系数βs的新算法。

2 基于四叉树分解的耦合系数估计方法

2．1 同构性的度量

在非均匀MRF中，耦合系数不是一个常数，是随着图像中局部的纹理特征而变化的。耦合系数表征了图像的同构性。在图像中灰度值分布散乱的区域，其同构性比较弱，耦合系数也就较小；而在图像的“块”较大的区域，同构性比较强，耦合系数比较大。图2显示了耦合系数和图像特征之间的关系。

图2 耦合系数与图像特征的关系Fig．2 Relation of isomorphic coefficient and image feature

在同一幅图像中，耦合系数往往β不是均匀分布的。如图3中的耦合系数随着图像的散乱程度从左到右逐渐变大。图4为图3的耦合系数的图像表示。

图3 散乱程度渐变的图像Fig．3 Scattered degree gruadually changed image

图4 耦合系数的图像表示Fig．4 Isomorphic coefficient image

通过观察发现在同构性小的区域，在进行初始分割后，其边缘信息比较丰富。因此用边缘信息的丰富程度，来度量图像在局部的同构性。具体做法如下：假如Mi为图像的一个子m×m的子块，di为该子块内边缘点的个数，定义耦合度为：

其中τ1为调节因子，它可以调节边缘信息在计算耦合度时的权重。

2．2 基于四叉树分解的耦合系数估计方法

四叉树分解的基本思想是首先将图像分为4个大小相等子块，在每个子块里面计算其图像特征（如均方差），如果此特征小于某个给定的域值，则再将该子块划分为4个相同大小的子块，如此循环，直到子块的大小达到预先给定的最小值为止。

这里以耦合度来作为图像特征，进行四叉树分解，这样就可以将耦合度比较大的区域分成比较大的子块，耦合度比较小的区域被分解成比较小的子块。在分解之前先进行一次基于均匀MRF的预分割，迭代少数几次即可。采用递归的算法，进行分解。以下是算法的步骤：

Step1：用基于均匀MRF的图像分割方法，迭代10～20次，对图像进行预分割；

Step2：对预分割后的图像I进行初始划分，把图像分为4个相同大小的子块I1，I2，I3，I4， 如果Ii的尺寸大于给定的最小尺寸，则转到step3，否则退出程序；

Step3：依次计算 I1，I2，I3，I4内的耦合度，如果子块 Ii的耦合度 βi小于给定域值 βT，则令 Ii等于 I，转到 step2。

图5 Lena图的四叉树分解Fig．5 Quad-tree decomposing of image Lena

图5显示了Lena图的四叉树分解。由图5可以看出，对图像进行四叉树分解之后，同构性小的区域被分成比较小的子块，同构性比较大的区域被分成了比较大的区域。因此可以用子块的大小来描述耦合系数的大小。由于耦合系数的取值一般是在区间[0．1，2．4]上取值，将区间进行均匀划分，对应不同的子块尺寸。表1给出了耦合系数和子块尺寸之间的对应关系。

表1 子块尺度与耦合系数的关系Tab.1 The relation of the subblocks’sizes and isomorphic coefficient

3 实验与分析

为了验证本文算法的有效性，我们对两幅256×256灰度图像分别用传统的基于MRF的分割方法和本文提出的方法进行了分割。程序的运行平台为赛扬2．66 CPU，512 MB内存，VC++6．0环境。本文的马尔可夫随机场求解方法为模拟退火算法，边缘检测算子为Sobel算子，预分割时的耦合系数取常数1．2。基于马尔可夫随机场的图像分割要用到两组重要的参数，及每个类别λ的均值μλ和方差σλ来。为了精确起见，本文采用样本训练的方法得到。如图6所示，选取方框中的特征块作为样本，得到每种纹理的均值和方差。分割模型中参数的取值都取经验值，其中初始温度T=6，温度调节因子α=0．95，加权系数 τ1=0．08。 从图 6（c），（d），（e），（f）可以看出，在图像预分割以后再进行四叉树分解，可以将图像的边缘较丰富的区域分成比较小的方块，而边缘少的区域被分解成比较大的方块。而小的方块对应小的耦合系数，这样在反复迭代中就能很好的保护边缘。

图6 待分割图像及其四叉树分解Fig．6 Original images and their quad-tree decomposed Images

文中的分割结果以及传统的分割结果如图7所示。

图7 分割结果Fig．7 Result of segmentation

从实验结果可以看出，传统的基于均匀MRF的分割方法中耦合系数过小容易产生较多孤立点（如图7（b）以及图7（e）中圆圈内所示），而耦合系数过大又不能很好的保持边缘（如图 7（c）以及图 7（f）中圆圈内所示）。而本文的分割方法采用了自适应的耦合系数估计方法，从而能够达到更为细腻的分割效果（如图 7（a）以及图 7（d）所示），这充分证明了文中方法具有较强的自适应性和鲁棒性。

4 结 论

首先简要阐述了基于非均匀马尔可夫随机场的图像分割原理及基本方法，然后从对耦合度的研究出发，提出了一种基于四叉树分解的耦合系数估计方法，并将此估计方法与基于马尔可夫随机场的图像分割算法相结合进行了数值实验。实验表明，本文方法与传统的基于马尔可夫随机场的图像分割算法相比效果更好，具有更好的自适应性。

[1]ZHANGYong-yue，Smith S，Brady M．Hidden Markov random field model and segmentation of brain MR images[M]．FMRIB Technical Report TR00YZ1 Oxford University，2000．

[2]Gu D B，Sun JX．Emimage segmentation algorithm based on an inhomogeneous hidden MRF model[C]//IEE Proc．-Vis．Image Signal Process．，2005．

[3]ZHANG Yong-yue，Brady M，Smith S．Segmentation of brain MR image trough a hidden markov random field modle and the expection-maximination algorithm[J]．IEEE Transactions on Medical Imaging，2006，20（1）：45-57．

[4]Geman S，Geman D．Stochastic relaxation， Gibbs distributions and the Bayesian restoration of images[J]．IEEE Trans．Pattern Anal，1984，26（9）：721-741．

[5]Derin H，Elliott H．Modeling and segmentation of noisy and textured images using Gibbs Random Fields[J]．IEEE Trans，Pattern Anal．Machine Intell，1987，9（1）：39-55．

[6]胡阳涟．基于马尔可夫随机场的图像分割研究[D]．西安：西安理工大学，2008．