钢悬链式立管涡激振动疲劳损伤参数分析

高 云，宗 智，周 力，曹 静

（1大连理工大学 工业装备与结构国家重点实验室，辽宁 大连116024；2大连理工大学 运载工程与力学学部，辽宁 大连116024；3中国海洋石油总公司研究中心，北京100027）

1 引 言

当海流流过立管时，由于结构的存在，便会产生流动分离现象，从而发生周期性的旋涡脱落和尾流。周期性的旋涡脱落会在立管上产生周期性的力，从而使立管发生振动，通常称之为涡激振动。

立管的振动又会对流场产生影响，使旋涡增强，阻力增加。这种涡激振动是小尺度部件流固耦合现象的体现。当旋涡脱落频率与立管固有频率接近时，将引起立管的强烈振动，旋涡的脱落将被立管的振动所控制，从而使旋涡的脱离和立管的振动具有相同的频率，发生“锁定”（lock-in）现象。Lock-in现象产生并不会马上对立管产生断裂破坏，但会对立管产生疲劳损伤。

控制立管的疲劳损伤是立管设计中的一个关键性问题。在稳定的波浪和海流等环境载荷作用下，导致立管产生疲劳损伤的主要因素有：海流引起的立管涡激振动以及波浪引起的浮体运动所导致的立管的疲劳损伤，对于某些吃水较深的浮体，浮体也有可能产生涡激振动，从而引起立管产生疲劳损伤[1]。

关于立管的振动响应以及疲劳损伤，国内外已有很多学者进行了相关研究。Wanderley等[2]采用了尾流阵子法对作用在海洋立管上的涡激载荷进行了分析。Vaz等[3]通过建立的三维索模型，对海洋立管在剪切流中的运动响应进行了分析。郭海燕等[4]以尾流振子模型为基础对海洋输油立管涡激振动响应进行了分析。薛鸿祥等[5]对非均匀来流下深海张紧式立管的涡激振动进行了研究。王一飞等[6-7]将深海立管简化为细长张力梁模型，并对其疲劳损伤进行了分析。潘志远等[8-9]将变参数受拉柔性梁的有限元模态分析与涡激振动预报结合在一起，建立了变参数柔性立管的横向涡激振动预报模型。高云等[10-11]就波浪对立管产生的浪致疲劳损伤以及平台涡激振动引起的立管的疲劳损伤做了相关研究。

从目前国内外的研究现状来看，大多研究都是基于浅水立管、细长式张紧立管进行研究的，而对于深海中钢悬链式立管的涡激振动产生的疲劳损伤，则研究较少。本文先是对钢悬链式立管进行了模态分析，得到立管的模态特性，再依据模态叠加法得到立管的涡激振动疲劳损伤，接着对立管以及环境的相关参数进行了疲劳损伤参数敏感性分析，并得到了一些有用的结论。

2 设计理论

2.1 钢悬链式立管振动简化模型

立管按照其工作环境的水深不同可分为浅水立管和深水立管。深水立管与浅水立管的最明显的不同在于：深水立管的几何上的大尺度将引发非线性的振动问题、浮体与立管间的运动耦合等问题。立管从本质上又可分为刚性立管和柔性立管，混合立管是两者的组合。海洋立管具有多种可能的结构，如顶部张紧式立管（TTR），钢悬链式立管（SCR），惰性S立管，陡峭型S立管，惰性波浪立管和陡峭型波浪立管等。

本文所分析的立管为钢悬链式立管，因钢悬链式立管通常是处在深水的工作环境中，立管的长度和直径之比很大，所以必须得考虑到立管的柔性特征。在模型选取过程中，参考了自由悬挂管线规范[12]（如表1所示）。由于本文所分析的立管的长度和直径的比值远大于200，再加上悬链式立管的几何非线性特征，所以在实际工作过程中，立管所表现出来的力学性质更切近索的特性。因此，在分析过程把钢悬链式立管作为张力索来处理。

表1 管线L/D变化时所对应的响应特性描述Tab.1 Response characteristics description of riser when L/D varies

2.2 立管模态分析理论

本文所计算的钢悬链式立管可简化为：两端铰接的线性变化张力索。根据文献[13]，立管的第n阶固有频率ωn可表示为：

上式中，L为立管的长度，n为模态阶次，s为沿立管轴线方向的坐标，T()s是坐标为s处的有效张力，所谓有效张力即为考虑了立管内部流体和外部流体压力效应后的张力。mt()s为单位长度的总质量。本文计算的立管的总质量应该包括立管的干重、内部液体的质量以及外部流体的附加质量三个部分，表达如下：

上式中，ρ，ρi和ρw分别为立管材料的密度、内部液体的密度以及外部液体的密度；Do，Di和De分别为立管的外径、内径以及外面绝缘层的直径，εin为立管的初始应变（通常取一个很小的值或为0），CI为外部流体的附加质量系数。

上式中，w为单位长度立管的水中重量，V0为立管在海底触地点处张力的垂直分量，T0为立管在海底触地点处张力的水平分量。

根据文献[13]，立管第n阶模态振型可由下式确定：

2.3 立管涡激振动疲劳损伤理论

本文将钢悬链式立管按照其张力和质量的分布拉直后简化为两端铰接的索模型，并建立如图1所示的直角坐标系。

假设坐标原点位于立管底部与海底的接触点上，Z方向为顺流方向，X方向为铅直方向，X，Y，Z三个方向形成右手直角坐标系。建立如下控制方程[13]：

式中，R包括结构阻尼和流体阻尼；T为张力；P x,( )t为升力分布，可表示为：

图1 立管坐标系示意图Fig.1 Schematic diagram of riser’s coordinate system

式中，ρw为海水密度；D为立管水动力作用直径；V()x为x处

式中，Lr为r阶模态的能量输入区域；为模态水动力阻尼；为模态结构阻尼。根据相关文献[14]，设损伤是高斯过程，在x处、r阶模态的固有频率ωr对应的损伤可由瑞利公式计算：以下给出第r阶模态响应造成的疲劳损伤计算公式，可表示为：

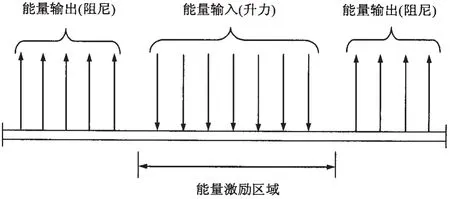
图2 模态能量平衡Fig.2 Modal power balance

式中，σi,rms为x处的第r阶模态响应均方根应力；T表示一年内的时间；Γ为伽马函数，可表示为：

结构在x处的总疲劳损伤为：

3 模态分析数值验证

取一典型的立管模型，此时立管的水动力半径、外径以及内径分别为：0.355 6、0.355 6以及0.320 6 m（详细参数如表2所示），对该立管的模态参数进行了理论计算以及数值计算。

理论计算是依据前面的公式进行了计算。数值计算是在ANSYS中采用了PIPE59单元进行了模拟。PIPE59单元能够设置波浪力、流体力以及浮力载荷，质量矩阵可包含附加质量、内部流体质量以及附加装置质量。外径与壁厚可通过DO、TWALL来设定，内部流体以及外部装置质量可通过CENMPL设定，附加水质量以及浮力可通过CI与CB设定。

图3给出了前6阶固有频率的对比结果；图4给出了前6阶模态振型的对比结果；图5给出了前6阶模态曲率的对比结果（注：图中横坐标为立管的相对位置，假设坐标原点在下端点）。由图可以看出模态分析计算结果吻合良好。

表2 立管基本参数Tab.2 Basic parameters of riser

图3 立管固有频率Fig.3 Natural frequencies of riser

图4 立管模态振型Fig.4 Mode shapes of riser

图5 立管模态曲率Fig.5 Mode curvatures of riser

4 涡激振动疲劳损伤分析

假设立管工作环境的水深为1 500 m，分析过程中考虑的是一百年一遇的长期环流。如图6所示，采用归一化系数的方法来描述流速剖面。纵轴为距海底的垂直高度，横轴为在对应此高度处的流的速度与表面流的速度的比值。

图6 流速分布图Fig.6 Current velocity profile

本文针对不同的流剖面系数、立管壁厚、立管外径、内部介质以及抑制立管涡激振动疲劳损伤的螺旋状列板（螺旋状列板通过不断改变径向的来流分离角度扰乱旋涡的空间相关长度，从而削弱旋涡强度并达到减小升力的目的）长度进行了疲劳参数敏感性分析，以下依次给出立管out-of-plane方向的分析结果。

图7 不同流剖面对应的年疲劳损伤曲线Fig.7 Fatigue damages per year of different velocity profiles

4.1 流速剖面参数影响分析

表面流速分别取0.5 m/s、0.6 m/s、0.7 m/s以及0.8 m/s，流速剖面系数如图6所示。在此计算过程中没有采用螺旋状列板抑制装置。立管的外径以及内径分别为：0.355 6以及0.320 6 m，内部流体为油。采用上述参数设置，得到立管随轴线方向的年疲劳损伤率如图7所示。

4.2 立管壁厚参数影响分析

立管壁厚分别取为0.012 5、0.017 5、0.022 5以及0.027 5 m，表面流速取为0.5 m/s，流速剖面系数如图6所示。在此计算过程中没有采用螺旋状列板抑制装置，外径取为0.355 6 m，内部流体为油。采用上述参数设置，得到立管随轴线方向的年疲劳损伤率如图8所示。

4.3 立管外径参数影响分析

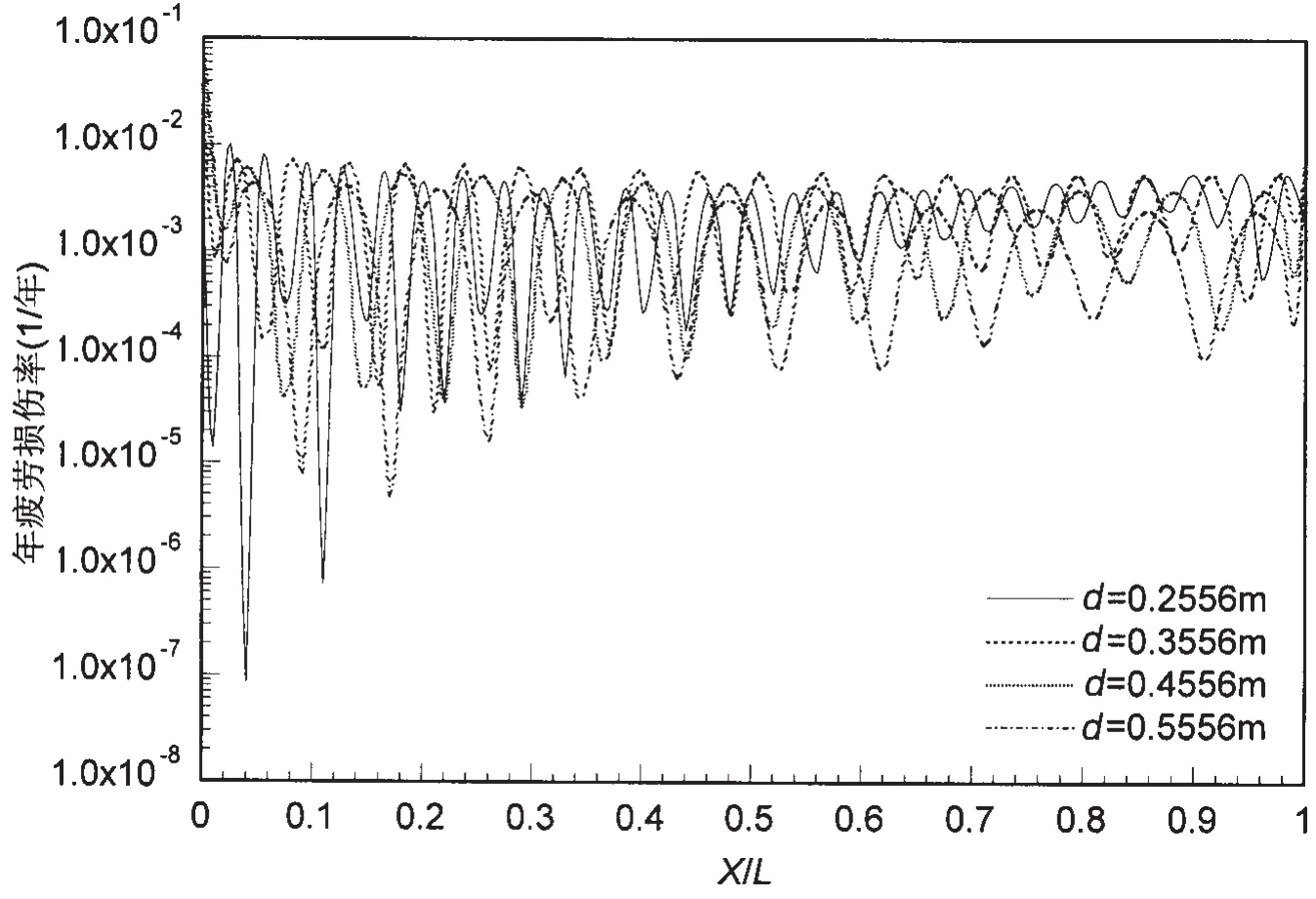
图9 不同外径对应的年疲劳损伤率Fig.9 Fatigue damages per year of different outside diameters

立管外径分别取为0.255 6、0.355 6、0.455 6以及0.555 6 m,表面流速取为0.5 m/s，流速剖面系数如图6所示。在此计算过程中没有采用螺旋状列板抑制装置，壁厚取为0.017 5 m，内部流体为油。采用上述参数设置，得到立管随轴线方向的年疲劳损伤率如图9所示。

4.4 内部介质参数影响分析

内部介质分别取为空气、油以及水，表面流速分别取0.5 m/s，流速剖面系数如图6所示。在此计算过程中没有采用螺旋状列板抑制装置。立管的外径以及内径分别为：0.355 6和0.320 6 m，采用上述参数设置，得到立管随轴线方向的年疲劳损伤率如图10所示。

4.5 STARKE长度参数影响分析

对不带STRAKE、带有立管长度轴线方向1/3的螺旋状列板、带有立管轴线方向2/3的螺旋状列板以及整个立管完全覆盖了螺旋状列板的四种情况进行分析。内部介质均取为油，表面流速分别取0.5 m/s，流速剖面系数如图6所示。立管的外径以及内径分别为：0.355 6和0.320 6 m，采用上述参数设置，得到立管随轴线方向的年疲劳损伤率如图11所示。

图10 不同内部流体介质对应的年疲劳损伤率Fig.10 Fatigue damages per year of different media

图11 不同STRAKE长度对应的年疲劳损伤率Fig.11 Fatigue damages per year of different STRAKE lengths

5 结 论

本文所建立的立管模型与以往建立的模型有所不同，采用的是索模型，而不是立管普遍采用的张力梁模型。由以上的分析计算可以得到如下结论：

（1）立管的疲劳损伤沿着轴线方向呈振荡性质，说明了立管涡激振动具有锁定现象，即当旋涡脱落频率与固有频率接近时，将引起立管的强烈振动。由图7-11可知：立管的最大疲劳损伤通常出现在上端与平台相连接或是下端与井口相连接的接口处，即立管的边界区域通常会出现应力集中现象。

（2）由图7可知：立管的疲劳损伤的峰值随着水流速度的增大呈上升趋势；由图9可得知：立管的疲劳损伤的峰值随着外径的增大呈上升趋势。由图8以及图10可知：立管壁厚的变化以及立管内部流体密度的变化对立管疲劳损伤大小影响不显著。

（3）由图11可知：加了螺旋状列板抑制装置的立管和没有加螺旋状列板抑制装置的立管的疲劳损伤相差很大，但是，加了占立管长度1/3、2/3的螺旋状列板的立管以及全部加上螺旋状列板的立管所受到的疲劳损伤则很相近。

[1]黄维平,李华军.深水开发的新型立管系统-钢悬链线立管（SCR）[J].中国海洋大学学报,2006,36(5):775-780.

[2]Wanderley J B,Levi C.Vortex induced loads on marine risers[J].Ocean Engineering,2005,32:1281-1295.

[3]Vaz M A,Patel M H.Three-dimensional behavior of elastic marine cables in sheared currents[J].Applied Ocean Research,2000,22:45-53.

[4]郭海燕,傅 强,娄 敏.海洋输液立管涡激振动响应及其疲劳寿命研究[J].工程力学,2005,22(4):220-224.

[5]薛鸿翔,唐文勇,张圣坤.非均匀来流下深海立管涡激振动响应研究[J].振动与冲击,2007,26(12):10-14.

[6]Wang Yifei,Wu Xiaoyuan,et al.Effect of elastic modulus on the VIV-induced fatigue damage in deep sea risers[J].Journal of Ship Mechanics,2007,11(6):867-878.

[7]王一飞,潘志远,黄小平,崔维成.深海立管涡激振动疲劳损伤影响因素分析[J].船舶力学,2006,10(5):76-83.Wang Yifei,Pan Zhiyuan,et al.Effects of various factors on the VIV-induced fatigue damage in deep sea risers[J].Journal of Ship Mechanics,2006,10(5):76-83.

[8]Pan Zhiyuan,Cui Weicheng,et al.A prediction model for vortex-induced vibration of slender marine risers[J].Journal of Ship Mechanics,2006,10(3):42-52.

[9]潘志远,崔维成,刘应中.低质量—阻尼因子圆柱体的涡激振动预报模型[J].船舶力学,2005,9(5):115-124.Pan Zhiyuan,Cui Weicheng,Liu Yingzhong.A predicting model for self-excited VIV of a circular cylinder at low massdamping[J].Journal of Ship Mechanics,2005,9(5):115-124.

[10]高 云,周 力,宗 智,曹 静.平台涡激运动造成的立管疲劳损伤研究[J].中国海洋平台,2009,24(5):41-46.

[11]高 云,宗 智,周 力,吴宗铎,曹 静.钢悬链式立管的浪致疲劳[J].大连海事大学学报,2010,36(2):1-5.

[12]DNV,DNV-RP-F105.Free Spanning Pipelines[S].Norway:GCS AS,March 2002:63-65.

[13]Blevins R D.Flow induced vibration[M].New York:Van Nostrand Reinhold Company,1977:21-54.

[14]Wilson J F.Dynamics of offshore structure[M].New York:John Wiley&Sons,inc,2002:72-75.