转化思想是解题的一把金钥匙
2012-03-15海伦市第二中学
✿海伦市第二中学 郭 媛
转化思想是一种重要的数学思想,它蕴涵着极其丰富的内容,应用非常广泛.在解数学题时,运用转化思想可化繁为简,把握解题的关键,突破解题的难点,探明解题的思路,获得新颖、独特的解题方法,从而提高解题的能力.可见,转化思想确实是解题的一把灵巧的金钥匙,现举例说明如下.
一、一般问题特殊化
例1:方程(m+1)x4-(3m+3)x3-2mx2+18=0对任何实数m都有一个共同的实数解,试求这个实数解.
分析:本题应抓住两个关键词:一是“任何实数”,二是“一个共同的解”,这样就可以把一般问题转化成特殊问题来解.
解:因为m为任何实数,不妨取m=-1和m=0两种情形,将m=-1代入原方程,得:2x2-18=0,
解这个方程,得:x=±3;
将m=0代入原方程,得:x4-3x3=0,
解这个方程,得:x=0或x=3.
因为这两个方程只有公共解x=3,所以方程共同的实数解是x=3.
二、不等问题相等化
例2:已知不等式a2+b2+c2+4≤ab+3b+2c,求满足不等式的实数a、b、c的值.
分析:一个不等式,三个待定未知量,不免令人困惑,但仔细揣摩条件,变换思考角度,不难想到向相等方面转化.
解:因为a2+b2+c2+4≤ab+3b+2c可变形为:
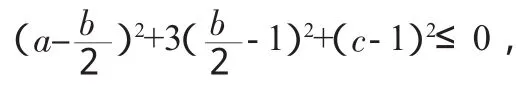
所以a=1,b=2,c=1.
三、方程问题不等式化
例3:一个边数是奇数的凸多边形中,除两个内角外,其余内角和为2 390°,求这个多边形的边数.
分析:此题如用方程解,难于下手,如根据多边形内角和定理及内角的取值范围来,求边数的取值范围,可迎刃而解.
解:设这个多边形的边数为n,由于多边形每个内角大于0°且小于180°,根据多边形内角和定理得:2 390°<(n-2)×180°<2 390°+180°×2,
又因为n是奇数,故n=17,这个多边形是17边形.
四、函数问题方程化
例4:已知抛物线y=x2-5mx+4m2(m为常数),求证:此抛物线与x轴一定有交点.
分析:要证抛物线与x轴有交点,可以转化成证明一元二次方程一定有实数解的问题.
解:若x2-5mx+4m2=0,
则Δ=(-5m)2-16m2=9m2≥0,
即一元二次方程x2-5mx+4m2=0有实数解,
故知抛物线y=x2-5mx+4m2与x轴一定有交点.
五、正面问题反面化
例 5:设三个二次方程 x2+4mx+4m2+2m+3=0,x2+(2m+1)x+m2=0,(m-1)x2+2mx+m-1=0,它们中至少有一个方程有实根,求m的取值范围.
分析:此题从正面入手,须要分多种情况进行讨论,运算相当繁冗,不如变换思考角度,从反面突破.
解:若三个方程均无实数根,则:
Δ1=(4m)2-4(4m2+2m+3)<0,
Δ2=(2m+1)2-4m2<0,
Δ3=4m2-4(m-1)2<0.
所以符合题意的m的取值范围为:

六、变量问题常量化
例6:解方程:x3+10x2+25x+4=0.
分析:这是关于x的三次方程,想通过降次解出x很不容易,若把常量a视为变量,把变量x视为常量,问题可迎刃而解.
解:把原方程变为:x×52+(2x2+1)×5+(x3-1)=0.
解关于5的一元二次方程得: