利用CFD技术研究叶片斜度对贯流风机性能的影响
2012-03-15王银姣卢剑伟
王银姣, 卢剑伟, 江 斌, 高 才
(合肥工业大学机械与汽车工程学院,安徽合肥 230009)
贯流风机具有结构简单、体积小、噪音低及轴向长度可调的优点,在家用分体挂壁式空调器中有广泛应用[1]。影响贯流风机性能的结构参数很多,至今尚无成熟的设计理论。文献[2-7]采用流场可视化的方法,用毕托管、三孔圆探头等来观察贯流风机内偏心涡的位置和测量偏心涡总压,实验结果表明贯流风机的性能主要取决于偏心涡的位置和总压大小,从而为改进贯流风机的性能指明了方向。随着计算机存储量和计算性能的大幅提高,研究人员开始采用计算流体力学技术(CFD)模拟贯流风机的内部流场[8]。设备改进前进行CFD模拟不仅能方便地寻找相对最优的结构参数,增加实验的针对性,大大降低实验的次数和成本,而且可以缩短设计周期。文献[9]利用CFD方法研究了贯流风机偏心涡总压、进出口总压升与叶轮转速关系的相似定律。文献[10-15]利用CFD方法,考察了蜗舌位置、蜗舌间隙、进出口角等结构参数对贯流风机的影响。目前利用CFD技术考察多结构参数变化条件下贯流风机内部流场的研究很少[16],只有少数研究[1,17]从贯流风机内部流场分布来研究风机性能,揭示涡与声的关系[18-19]。因此,本文根据某企业空调用贯流风机提高风量及降噪的实际要求,利用CFD软件ANSYS CFX11.0,在贯流风机蜗壳形状不变的情况下,模拟不同叶片斜度下贯流风机的内部流场,考察多结构参数同时变化对贯流风机内部流场及性能的影响,最后通过实验来验证模拟的正确性。
1 方 法
图1所示为某空调用的贯流风机结构图,记为模型1。

图1 贯流风机结构图
针对模型1风机的实际要求,本文在保持蜗壳形状及相对叶轮位置不变的前提下,采取增大蜗舌间隙的方法对贯流风机进行改进。相对于叶片的传输角及高度,蜗舌间隙更能决定风机的性能[2]。文献[13]给出了合理的蜗舌间隙范围应为叶轮外径(D2)的6%~9%,增大蜗舌间隙,就必须减小D2,如保持叶片形状及大小不变,只能通过改变叶片位置实现。因此,引出与叶片位置联系紧密的叶片斜度α。
图2所示为叶片几何关系图,α是叶片中线端点A、B连线与端点A切线的夹角。已有研究发现外周叶片角β2减小会有利于总压系数的提高[3],因此将叶片斜度减小,分别取α为54°(模型1)、50.5°、49.5°、48.5°、47.5°、46.5°、42.5°,以确定贯流风机最佳效率和总压系数。

图2 叶片几何关系图
鉴于流道形状复杂,采用ANSYS ICEM CFD软件对计算域划分网格,且全部选用非结构化四面体网格。整个流域分为叶轮区的旋转域和非叶轮区的静止域,网格数量约为16×104时,计算精度满足要求,计算速度可以接受[15]。贯流风机流体域的网格分布如图3所示。模拟针对三维瞬态情况进行,采用标准k-ε湍流模型,对流项采用高级精度格式离散,瞬态项采用二阶-向后欧拉差分有限体积方法。
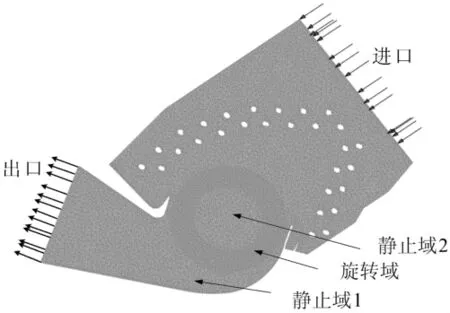
图3 贯流风机网格分布图
壁面和流固交界面采用壁面无滑移边界条件,参考压力为101.325 kPa,进出均为压力边界条件。文献[9]建议根据转速来确定时间步长,此处非稳态计算的时间步长设为8×10-5s,叶轮完成一个旋转周期需要约550个时间步长。已有研究表明,时间步长设为叶轮旋转周期的1/180即能满足精度要求[10],因此本文计算中选取的时间步长已足够小,能够捕捉到模拟过程中的细节现象。
为了考察模拟分析的有效性,利用焓差法(空调器)综合性能试验台[20],在国家标准的实验工况下[21],测量模型1和模型2物理样机,在不同转速(1 360、1 250、1 050 r/min)下的风量,并将其与CFD模拟结果进行对比,以验证仿真结果的正确性。
2 结果与讨论
2.1 风机性能系数
多数研究[6,16-17,22-23]经常通过流量系数φ、风机效率η、总压系数ψt来考察风机性能,这3个系数都是无量纲参数。
流量系数用来表征对应风机结构及其运行状态下风机输送流体的能力,可表示为:

其中,L为叶片轴向长度;D2为叶轮外径;U2为圆周速度,U2=πD2n/60;n为风机转速;Q为风机体积流量。
风机效率就是输送流体的有效功率与输入扭矩功率之比,可表示为:

其中,Δptot=ptot-outlet-ptot-inlet为风机总压升;ptot-inlet与ptot-outlet分别为进、出口处的总压力值;M为扭矩,M=9 549 P/n,P为风机额定制冷功率;ω为风机旋转角速度。
总压系数用来表征风机所能提供的最大总压升的能力,可表示为:

其中,ρ为空气密度。
不同α下风机性能系数及相关变量参数,见表1所列。随着叶片斜度的减小,内周叶片角β1增加,外周叶片角β2减小,叶轮外径D2减小,直径比D1/D2与蜗舌间隙ε增加。流量系数、风机效率及总压系数均在α=48.5°时达到最大,此时风机体积流量Q和总压升Δptot达到最大。
由(1)式、(2)式可知,风机体积流量Q与性能系数(φ,η)都成正比关系,即φ(或η)∝Q。而叶片外径D2是决定φ和ψt的重要因素,且呈二次反比关系,即φ(或ψt)∝(1/D2)2。由于在α=48.5°时风机性能系数最优,因此选该角度下模型,同时增大环带内径得到模型2作为改进模型,与模型1进行对比分析。
2.2 偏心涡
文献[7]最早在研究中提出偏心涡(eccentric vortex)的概念,在当时的贯流风机设计中,认为强度大的偏心涡可以形成一种密封屏障,以阻止风机出口处气流的回流。流体两进两出贯流风机叶轮,在近蜗舌处形成偏心涡,偏心涡的旋转方向与叶轮旋转方向相同,正是由于偏心涡的存在,排出的气流又回流到叶轮区,导致出口的流量减小,造成了能量的大量损失[14]。同时,蜗壳处也形成一个相似的涡,但涡的旋转方向与叶轮旋转方向相反且强度相对偏心涡较弱。在偏心涡核心,流体速度降低,导致偏心涡区域动压降低,从而使得其总压为负值。在出口处,叶轮对气体做功,气体相对速度增加,使得出口处静压回升,动压增大,总压增至最大。因此对比研究2种模型的总压与速度云图,对了解贯流风机内部流场分布及噪声源分析至关重要。

表1 不同α下风机性能系数及相关结构参数
取轴向中心截面进行分析,得到图4所示中心截面总压云图和图5所示速度云图。
由图4可见,不论是模型1还是模型2,均在贯流风机出口侧靠近蜗舌的地方有一个低压中心,形成了环流偏心涡。由进口至偏心涡区域,流体静压逐渐降低,在偏心涡中心达到最低。正是这种压力梯度使得气流做横贯叶轮的运动,形成贯流区。实验发现,偏心涡的大小、位置及强度对风机性能影响较大,而涡的这些参数又会受到风机几何参数和运行工况的影响[7]。由图4可以发现,相对模型1而言,模型2的偏心涡位置更加靠近蜗舌,大小基本一样,但强度明显减小。这就导致了模型2中蜗壳处压力分布范围向风机出口处延伸,而且分布更加均匀,气流更加平稳快速。结合图5对比可知,模型2在旋转域及静止域内速度分布范围明显比模型1广,速度梯度减小,从而减小气流对叶片的冲击作用,使得内部流场分布更加均匀,减小运行噪声。除此之外,模型2出口处气流速度比模型1明显增大,这会直接增加贯流风机出口送风量。有研究通过高速摄像机发现[10],风机转速增加会使偏心涡移向涡舌并且减小涡的规模。结合本文分析的结果,可以推断偏心涡的位置及强度受风机转速和蜗壳、叶片几何结构参数共同制约。

图4 模型1与模型2总压对比图
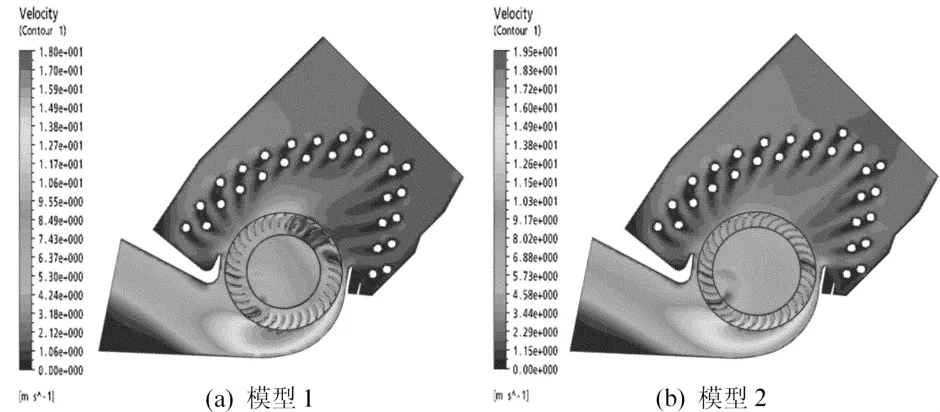
图5 模型1与模型2速度对比图
2.3 总压分布
图6所示为总压ptot沿R=30 mm的圆周分布,特征角分别对应图1中的角度。图6中θtr表示蜗舌处回流结束位置;θt表示蜗舌所在位置;θvc表示最邻近偏心涡位置;θcr表示蜗壳处回流开始位置;θc表示蜗壳所在位置。对于模型1和模型2而言,其θtr、θt、θcr、θc基本相同。
这些点将贯流风机流场分为4段:θtr—θvc偏心涡分隔段、θvc—θcr流体出口段、θcr—θc蜗壳涡分隔段及θc—θtr流体进口段。由图6可见,(θvc1-θt)>(θvc2-θt)表明模型2的偏心涡比模型1的偏心涡更靠近蜗舌;(θvc1-θtr)>(θvc2-θtr)表明模型1的偏心涡分隔段大于模型2的偏心涡分隔段。偏心涡分隔段越大,偏心涡引起的回流越多,能量损失越大。一般情况下,涡越靠近蜗舌,贯流风机性能越好[11]。同时,由于θvc1>θvc2,使得(θcr-θvc1)<(θcr-θvc2),说明模型1流体出口段有效过流宽度小于模型2出口段有效过流宽度。模型1在0°<θ<40°及θc<θ<360°(360°与0°重合)这段区间内,流体的总压均低于40°<θ<θtr区间内流体总压,与图5中进口段靠近蜗壳侧速度较低区域相对应,这是因为模型1该区间速度较低,导致其总压偏低。
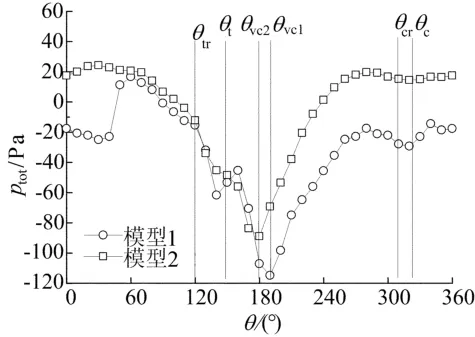
图6 R=30 mm总压圆周分布
对比发现,改造后风机模型2总压周向分布连续性及平滑性都要好于模型1,因此优化叶片斜度有利于总压性能的提高。
2.4 风机出口处性能
图7、图8所示分别2种模型出口段总压、速度分布。可以看出,在相同监测点(对应图1出口段监测点),模型2出口总压和速度均大于模型1的相应值,离叶轮越远其值越低。这是由于模型2进口段和出口段有效过流宽度增加,出口流速增大[14],总压增大,风机流量增加。模型2风量为753 m3/h,比模型1的689 m3/h提高了9.3%。因此在同等条件下,可以用较低的风机转速满足风量要求,降低风机噪声。

图7 模型1与模型2出口总压对比

图8 模型1与模型2出口速度对比
2.5 涡流黏度
文献[3]指出,贯流风机的性能与叶片上涡的脱落密切相关,脱落的小尺度涡最终会发展成一个大尺度的偏心涡,恶化贯流风机的性能。如图9所示,可以看出,模型1叶轮进口段约有5个叶栅通道内涡流黏度较大,这是因为在这些叶栅通道内形成了脱落涡,这些脱落涡迅速掺混,形成了大尺度的涡结构,由于流体黏性作用,降低了这些叶栅内流体速度,与图5中进口段靠近蜗壳侧速度较低区域相对应,而这个涡类似于一个大障碍物,阻碍进口气流进入叶轮,从而缩短了流体进口段有效过流宽度。而模型2(图9b)在进口段涡流黏度分布更均匀,没有脱落涡形成的大尺度涡,进口段流速分布平均。在低速流体机械中,进、出口段的部分流道中分离结构所引起的大尺度脱落涡结构,是流体流经叶片的主要气动噪声源[19]。因此优化叶片斜度,可以减少进口段脱落涡的形成,提高出口速度,同时降低风机噪声。
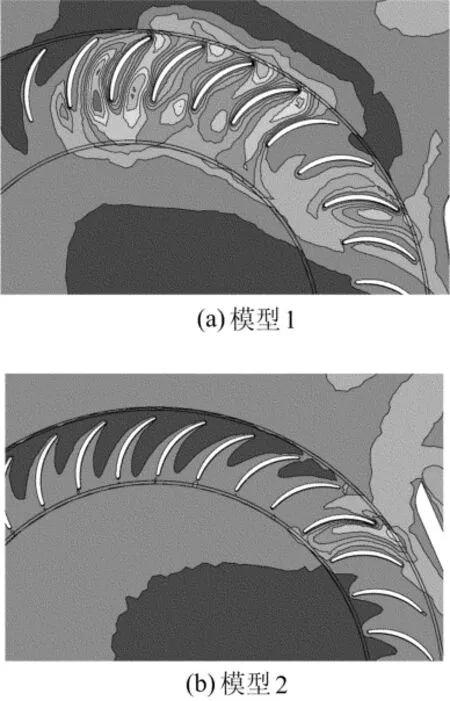
图9 模型1与模型2进风段涡流黏度分布图
2.6 实验与模拟结果对比
模型1和模型2实验与模拟风量对比,见表2所列。可以看出,在3种转速下,模型1和模型2的模拟风量与实验测量风量相对误差均在5%之内,模拟所用的模型和方法正确。

表2 实验与模拟风量对比 m3/h
3 结束语
采用CFD技术对某空调用不同叶片斜度贯流风机进行三维非稳态数值模拟,对比了改变叶轮几何结构参数的2种模型的内部流场分布。结果表明,贯流风机叶片斜度影响偏心涡的位置、大小、总压分布以及进口段脱落涡的产生。合理的叶片斜度,可以减少进口段脱落涡,提高出风口速度,增大风机流量,优化风机性能。焓差法风量实验验证了模拟结果的正确性。
[1] Li Y,Ouyang H,Tian J,et al.Discrete tonal noise investigation of the cross-flow fan with block-staggered impellers[J].Proceedings of the Institution of Mechanical Engineering,Part A:Journal of Power and Energy,2010,224(4):555-572.
[2] Murata S,Nisnihara K.An experimental study of cross flow fan:1st report,effects of housing geometry on the performance[J].Bulletin of the JSME,1976,19(129):314-321.
[3] Yamafuji K.Studies on the flow of cross-flow impellers:1st report,experimental study[J].Bulletin of the JSME,1975,18(123):1018-1025.
[4] Murata S,Nisnih4ara K.An experimental study of cross flow fan:2nd report,movements of eccentric vortex inside impeller[J].Bulletin of the JSME,1976,19(129):322-329.
[5] Matsuki K,Shinobu Y,Takushima A,et al.Experimental study of internal flow of a room air conditioner incorporating a cross flow fan[J].ASHRAE Transactions,1988,94(part 1):350-364.
[6] Porter A M,Markland E.A study of the cross flow fan[J].Journal of Mechanical Engineering Science,1970,12(6):421-431.
[7] Eck B.Fans[M].Oxford:Pergamon Press,1973:156-181.
[8] Dawes W N,Dhanasekaran P C,Demargne A A J,et al.Reducing bottlenecks in the CAD-to-mesh-to-solution cycle time to allow CFD to participate in design[J].Journal of Turbomachinery,Transaction of ASME,2001,123(3):552-557.
[9] Shih Y C,Hou H C,Chiang H.On similitude of the cross flow fan in a split-type air-conditioner[J].Applied Thermal Engineering,2008,28(14/15):1853-1864.
[10] Gebrehiwot M G,De Baerdemaeker J,Baelmans M.Nu-merical and experimental study of a cross-flow fan for combine cleaning shoes[J].Biosystems Engineering,2010,106(4):448-457.
[11] 张师帅,罗 亮,李伟华.基于CFD分析的空调用贯流风机的性能预测[J].流体机械,2008,36(5):18-20.
[12] 张 辉,高 才,刘向农,等.方腔内不同位置块状食品层流冷却数值研究[J].合肥工业大学学报:自然科学版,2010,33(4):495-497,509.
[13] 游 斌,区颖达.影响横流风机性能的各几何因素[J].风机技术,1997(6):22-25.
[14] 胡俊伟,丁国良,赵 力,等.贯流风机结构参数及工作特性的关联[J].上海交通大学学报,2007,38(7):1156-1160.
[15] 游 斌,周 拨,吴文新,等.多翼风机新型斜蜗壳与常规直蜗壳的对比研究[J].工程热物理学报,2006,27(2):235-237.
[16] Toffolo A,Lazzaretto A,Martegani A D.Cross-flow fan design guidelines for multi-objective performance optimization[J].Proceedings of the Institution of Mechanical Engineering,Part A:Journal of Power and Energy,2004,128:33-42.
[17] Toffolo A,Lazzaretto A,Martegani A D.An experimental investigation of the flow field pattern within the impeller of a cross-flow fan[J].Experimental Thermal and Fluid Science,2004,29:53-64.
[18] 孙晓峰,周 盛.气动声学[M].北京:国防工业出版社,1994:10-100.
[19] 刘 飞,王嘉冰,胡亚涛,等.贯流风机涡结构与噪声特性的数值研究[J].工程热物理学报,2009,30(1):44-46.
[20] 李雄林,曹小林,王 伟,等.焓差法空调器性能测试平台的研制[J].流体机械,2007,35(1):69-73.
[21] GB/T 7725-2004,房间空气调节器[S].
[22] Yamafuji K.Studies on the flow of cross-flow impellers:2nd report,analytical study[J].Bulletin of the JSME,1975,18(126):1425-1431.
[23] Lazzarotto L,Lazzaretto A,Martegani A D,et al.On cross-flow fan similarity:effects of casing shape[J]. ASME Journal of Fluids Engineering,2001,123:523-531.
