基于粗糙性惩罚的变系数纵向数据模型的参数估计

郭海兵,李连庆

(1.淮海工学院 理学院，江苏 连云港 222005；2.中国人民大学 统计学院，北京 100872)

0 引言

传统的线性模型

中，往往认为回归系数β是固定的，但是在一些问题中，这样的假设很不合适。例如在纵向数据中，β表示某种药品的边际效用，显然随着时间的变化，单位药品带来的效用是在不断的变化，甚至于病愈后这样的效用是负的。Hastie(1993)通过很多的例子来揭示模型(1)的不足之处，并据此提出了变系数线性模型

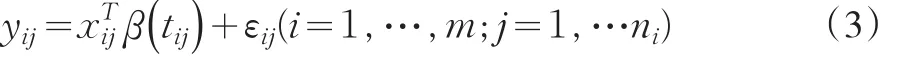
1 参数估计及其性质

2.1 一些符号标记

其中:

这里假设所有的样本信息都以提炼到模型之中了，误差项只是一组白噪声序列，也就是

1.2 参数估计

对于模型（5）中的变系数β() t的估计，通常使用非参数的方法。Fan(1999)和Xia(2004)等运用局部线性多项式

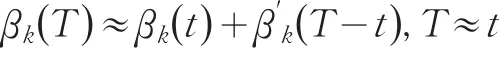
将问题转化成局部最小二乘估计，并且证实了具有很好的渐进性质，但是估计的过程中涉及到两个量——带宽（bandwidth）和权重（weight）的选择和优化是非常困难的事情。Hoover（1998）等人在使用了B样条的方法进行了估计，但是该法对节点t0的要求比较高，当节点的间隔不等距的时候，计算过程带来很大的困难。本文考虑如下基于粗糙性的惩罚似然函数的估计量

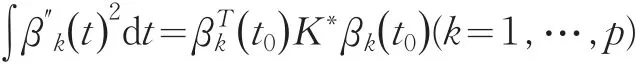
其中,q=n1+n2+…+nm,K1=…=Kp=K*,于是（7）式可以写成

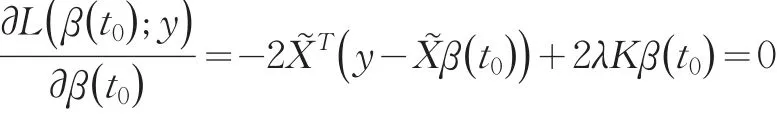
解之得

综上，可以得到如下结论：

定理1变系数纵向数据模型(5)关于粗糙性惩罚似然函数（8）的估计量为:

其中:

1.3 估计量的数字特征

定理2定理1中的估计量的期望和协方差阵分别为:

证明：由于

而

带入(10)式，可以得到(11)的前面部分。又因为

2 模拟计算

考虑模拟如下的模型：

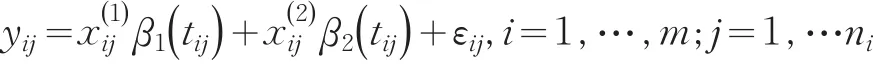
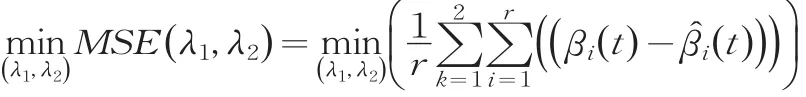
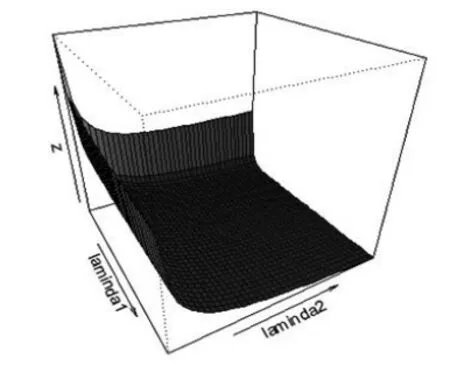
图1 光滑参数关于MSE的三维图

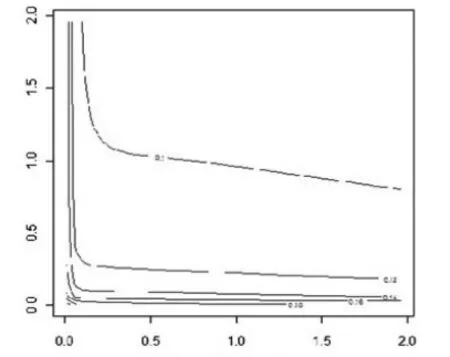
图2 三维等高线

图1和图2分别为光滑参数λ1,λ2关于MSE的三维图和等高曲线图。从中可以看出，MSE随光滑参数λ1和λ2的增加逐渐减少，并且当两者接近于2时候，即接近于稳定。因此，光滑参数的选择上可以运用网格搜索的方法来实现。

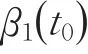
表1 均方误差关于me的比较

表1给出了不同的光滑参数组合下，分别进行30次、100次和200次模拟的得到MSE、MSE1和MSE2的平均值。从表1可以看出，随着模拟次数的增加，误差在逐渐的减少，随着光滑系数的增加误差也在减少；并且当λ1,λ2很小的时候，不同的组合，对于误差的影响较大；两者取值较大时，不同组合影响在减小。

图3 β1模拟结果

图4 β2的模拟结果

图3和图4分别是β1和β2的模拟结果，从左到右依次为30次、100次和200次模拟的平均值。其中实线为真实值，虚线为估计值。

[1]Hastie,T.J.,Tibshriani,R.J.Varying-Coefficient Model[J]J.Roy.Statist. Soc.,1993,(B55).

[2]Hoover,D.R.,Rice,J.A.,Wu,C.O.,Etal.Noparametric Smoothing Estimates of Time-Varying Coefficient Models with Longitudinal Data[J]. Biometrika,1998,(85).

[3]Fan,J.Q.,Zhang,W.Y.Statistical Estimation In Varying Coefficient Models[J].Ann.Statist.,1999，(33).

[4]Xia,Y.,Zhang,W.,Tong,H.Efficient Estimation for Semivarying-Coefficient Models[J].Biometrika，2004,(91).

[5]Li,Z.X.,Xu,W.L.,Zhu,L.X.Influence Diagnostics and Outlier Tests for Varying Coefficient Mix Models[J].Journal of Multivariate Analysis，2009,(100).

[6]Green,P.J.,Silverman,B.W.Nonparametric Regression Generalied Linear Model[M].London:Chapman and Hall,1994.

[7]唐庆国,王金德.纵向变系数模型中的减元估计法[J].中国科学A辑,2008，(38).