多传感器多目标系统误差融合估计算法
2012-03-15宋强
宋 强
(海军装备研究院,北京 100036)
熊 伟 何 友
(海军航空工程学院 信息融合技术研究所,烟台 264001)
多传感器多目标系统误差融合估计算法
宋 强
(海军装备研究院,北京 100036)
熊 伟 何 友
(海军航空工程学院 信息融合技术研究所,烟台 264001)
为解决多传感器组网系统的系统误差估计问题,基于多传感器多目标上报信息,研究并提出了一种多传感器多目标系统误差融合估计算法.算法构建了两级融合结构,即第一级对多传感器组合状态估计信息进行反馈融合以改善局部组合状态估计精度,从而间接改善系统误差的估计精度,而第二级对多目标系统误差估计信息进行融合以进一步提高系统误差的估计精度.蒙特卡洛仿真显示算法能有效融合利用多传感器多目标信息,实现多传感器系统误差的实时精确估计.
系统误差;传感器网络;误差配准;信息融合
近年来,随着目标探测、信号处理、数据链路通信等相关技术性能的提高,通过多传感器监视系统组网探测,可以使得系统在目标探测、航迹起始、跟踪精度、覆盖范围及可靠性等各方面都明显得到增强[1].但是由于传感器系统误差(偏差)的存在,系统实际跟踪效果往往得不到保障,甚至会严重降低多传感器系统的整体跟踪性能,因而如何有效估计并校准传感器在量测过程中的系统误差,对传感器系统误差估计(又称系统误差配准)技术进行深入研究具有重要的现实意义和较强的工程需求[2-5].
为解决上述问题,许多研究者都致力于传感器误差配准技术的研究,并相继提出了一系列实时系统误差估计方法.其中,文献[6]利用合作目标提供的实时高精度坐标,提出了一种单传感器系统误差协同配准算法;而在两部传感器配合进行误差配准理论研究方面,文献[7-8]基于传感器上报的单目标数据,并通过引入系统误差对目标状态向量扩维滤波的方法,实现对系统误差和目标状态的实时同步估计;为有效降低算法运算量,提高工程实用性,文献[9]通过对扩维的状态向量和系统误差进行解耦的方法,提出了两两传感器的系统偏差分离解耦估计方法,在降低算法系统耗时的基础上,实现了对系统误差和目标状态的实时和解耦估计;文献[10]论证了在两解耦滤波器初始参数设置之间符合一定关系条件下,文献[9]方法与扩维滤波估计算法的等效性,但当在非线性系统中或为解耦而需做出一定近似时,这一等价性也可能不成立,这就说明了文献[9]解耦估计算法性能对初值与非线性近似敏感,其估计性能不能得到保证;文献[11-12]通过对两部传感器构建伪量侧方程,利用多目标信息,实现了对传感器系统误差的序贯实时估计.然而,文献[6]算法的运用条件是待配准的单传感器,需选择位置分布合适并具有较高导航精度的飞机,并通过数据链实时获取飞机上导航设备提供的大地坐标,这使得算法在实际工程应用中具有较差的操作性.文献[7-10]所涉及的算法要求具有合作目标,本身都是基于两部传感器的,虽可扩展利用多部传感器信息,但是不能利用多目标信息进行融合估计.而文献[11-12]所提供的算法虽然利用到了多目标信息,但其亦未采用融合方法有效利用多传感器信息.
因而,基于多传感器多目标上报信息,本文构造并提出一种传感器系统误差的实时融合估计算法.该算法通过多部传感器的两两传感器组合来构建两级融合估计结构,即第一级对传感器组合估计信息进行反馈式融合来改善局部组合的状态估计精度,从而间接改善系统误差的估计效果,第二级对多目标信息进行融合以进一步提高系统误差的估计精度,以此有效融合利用多传感器多目标信息对传感器系统误差进行融合估计.
1 系统描述
假设由Ns个三维传感器对M个匀速直线运动目标进行同步组网探测,假定传感器i和j可组成第lij个探测组合,则共可形成个两两探测组合.传感器i和j在融合中心坐标系中的笛卡尔坐标分别为(ui,vi,wi),(uj,vj,wj),而传感器 i和j对目标的量测值分别为)和,且各传感器均具有一定的白色高斯量测噪声.
假设目标 t(t=1,2,…,M)在时刻 k的真实位置和速度分别为(xt(k),yt(k),zt(k))和,而第lij个传感器组合的测距离、方位和俯仰系统误差分别为(ΔRi,ΔRj),(Δθi,Δθj)和(Δηi,Δηj).
由此k时刻目标t的状态向量可描述为
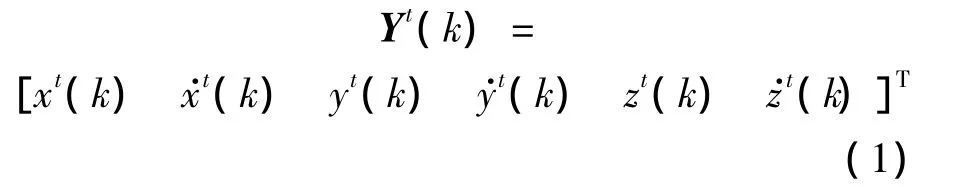
第lij个探测组合中,目标t在时刻k的系统扩展状态向量定义如下:

不失一般性地,目标t的系统运动状态方程可定义为
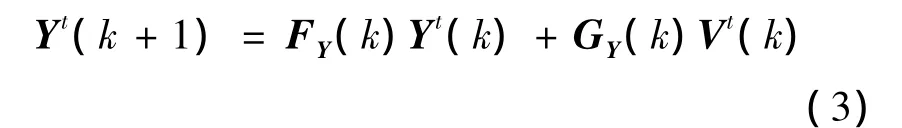
式中,FY(k)∈Rn,n是状态转移矩阵;Vt(k)是协方差为Qt(k)的白色高斯过程噪声,而GY(k)是其转移矩阵.
通常可以假设传感器系统误差为恒定量或者在较长时间内为慢变量,这样系统误差就可以描述为
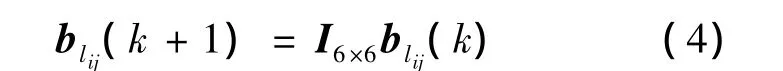
式中,I6×6表示6 ×6 的单位矩阵,且
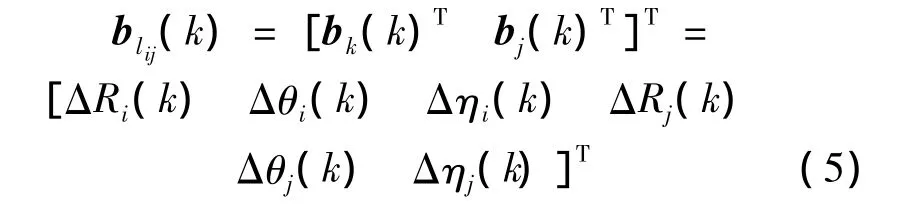
因此,第lij个组合中目标t的系统离散动态方程可以表示为
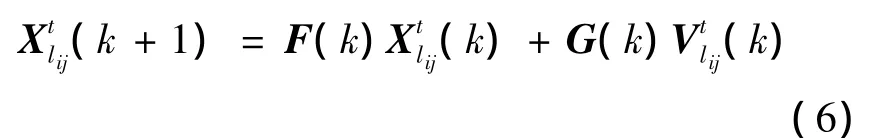
式中
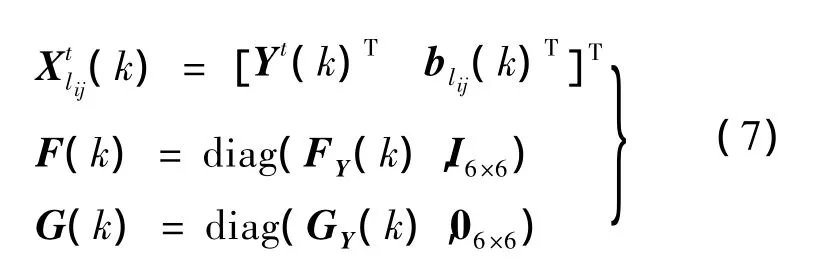
其中06×6表示6×6的零矩阵.
第lij个组合相应于目标t的量测方程可以定义为
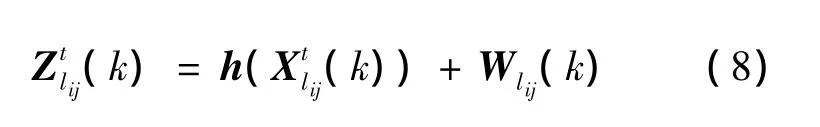
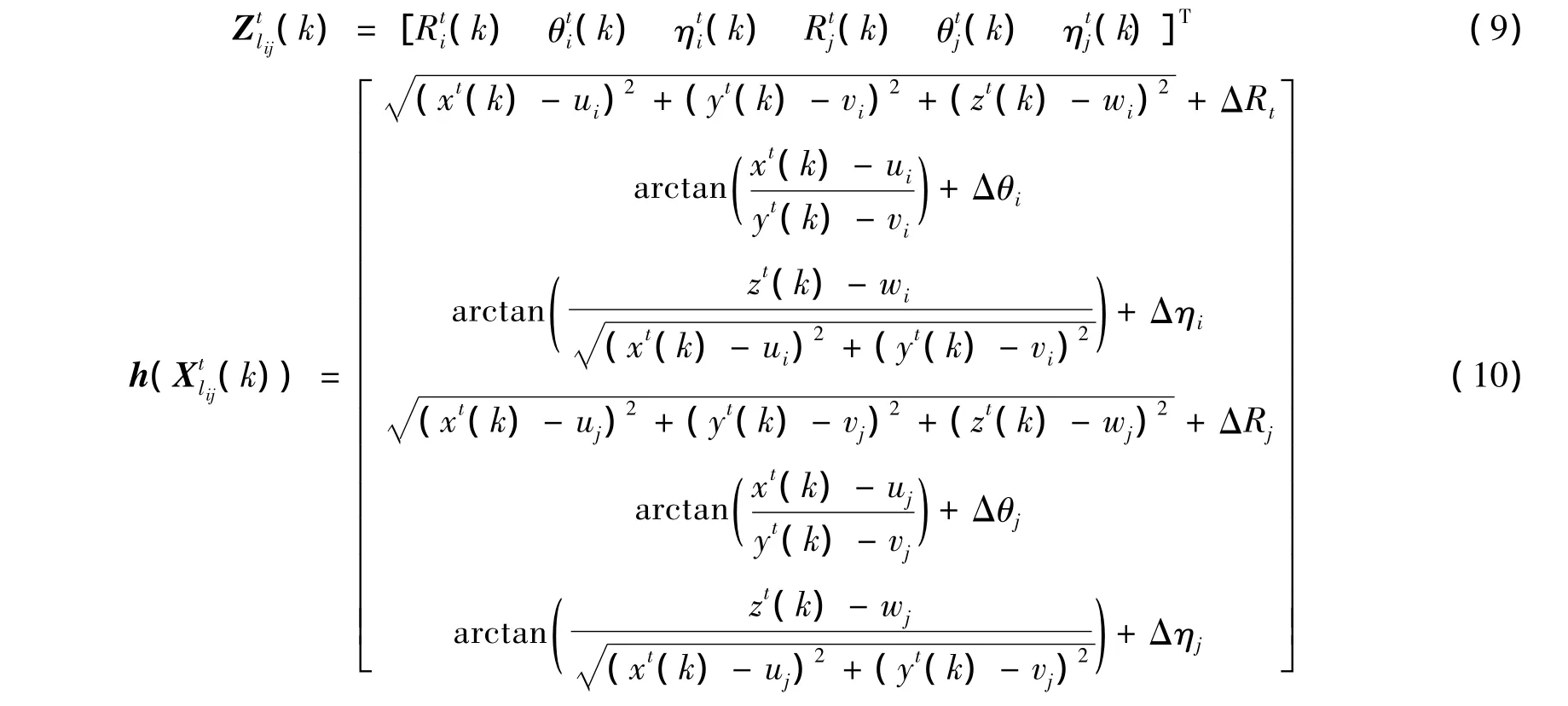
式中Wlij(k)为服从高斯分布的白色量测噪声,记Rlij(k)为其协方差.
2 多传感器多目标系统误差融合估计算法模型
2.1 局部组合节点系统误差估计模型
对于由传感器i和j构成的第lij个传感器组合,根据式(5)、式(7)中给出的状态方程和量测方程,可列出相应的实时滤波方程组,即第lij个局部组合节点对目标t目标状态与传感器i和j系统误差的联合实时估计为

其中h的雅可比矩阵是

2.2 多传感器组合估计信息反馈融合估计
如前所述,对于含有Ns个传感器的多传感器探测系统,基于传感器两两组合可构建L个估计组合,而各组合均可获得局部节点的系统误差与目标状态的联合实时估计,在每一时刻,各局部组合估计向量均含有对同一目标t的状态估计以及该组合传感器的系统误差估计信息维.
根据文献[1,13]中多传感器反馈式信息融合结构能改善局部估计性能的思想,可构建第一级融合结构,通过对各局部传感器组合估计进行融合,形成第一级融合结构的系统全局状态估计向量,并将系统融合信息反馈至下一时刻各局部组合节点的实时估计.
对于目标t,定义第一级融合系统全局状态估计包含对目标状态与Ns个传感器系统误差的系统估计,即
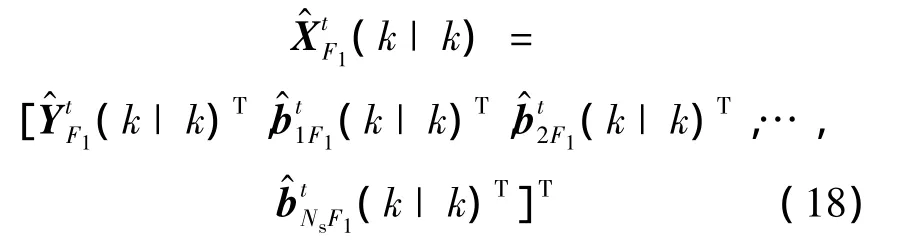
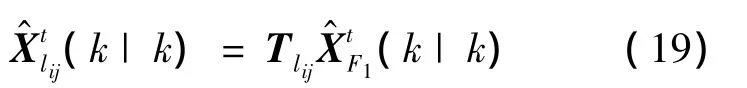
式中Tlij为全局状态向量到第lij个组合局部状态向量的空间映射,即第一级融合得局部状态空间转移矩阵,可描述为
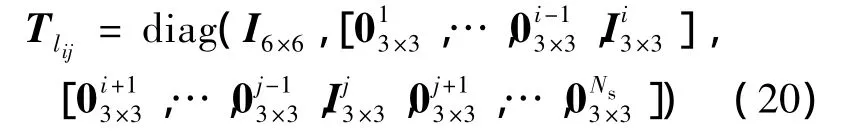
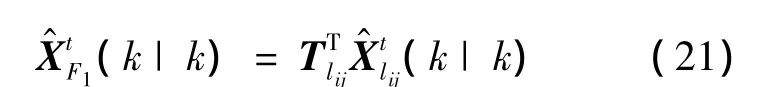
由于局部空间与全局空间之间状态维数的不一致性,若第lij个组合节点接收来自第一级融合结构融合中心的反馈,则局部节点状态估计的描述应该修改如下:
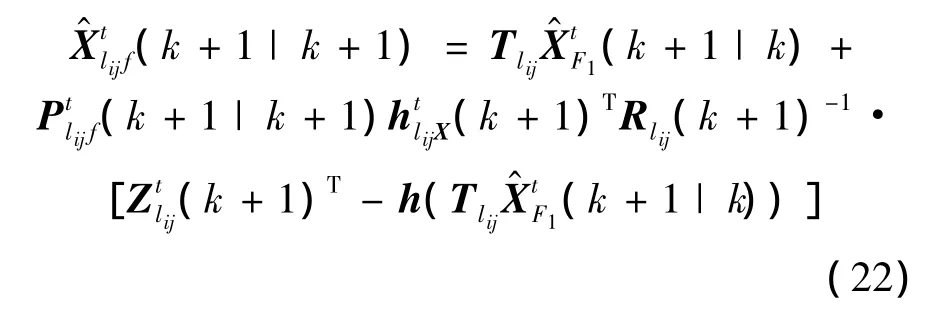
而
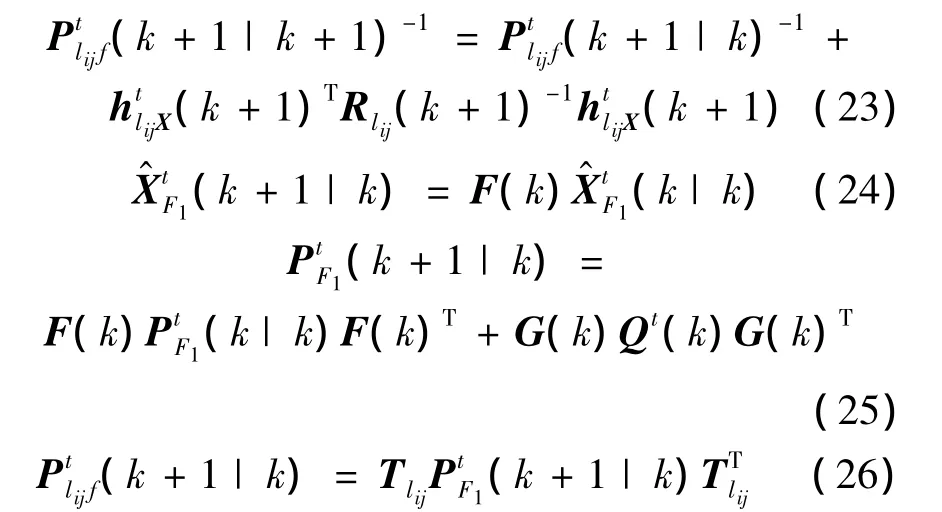
结合式(22)~式(26),不难得到第一级融合中心的系统状态估计和相应的协方差为
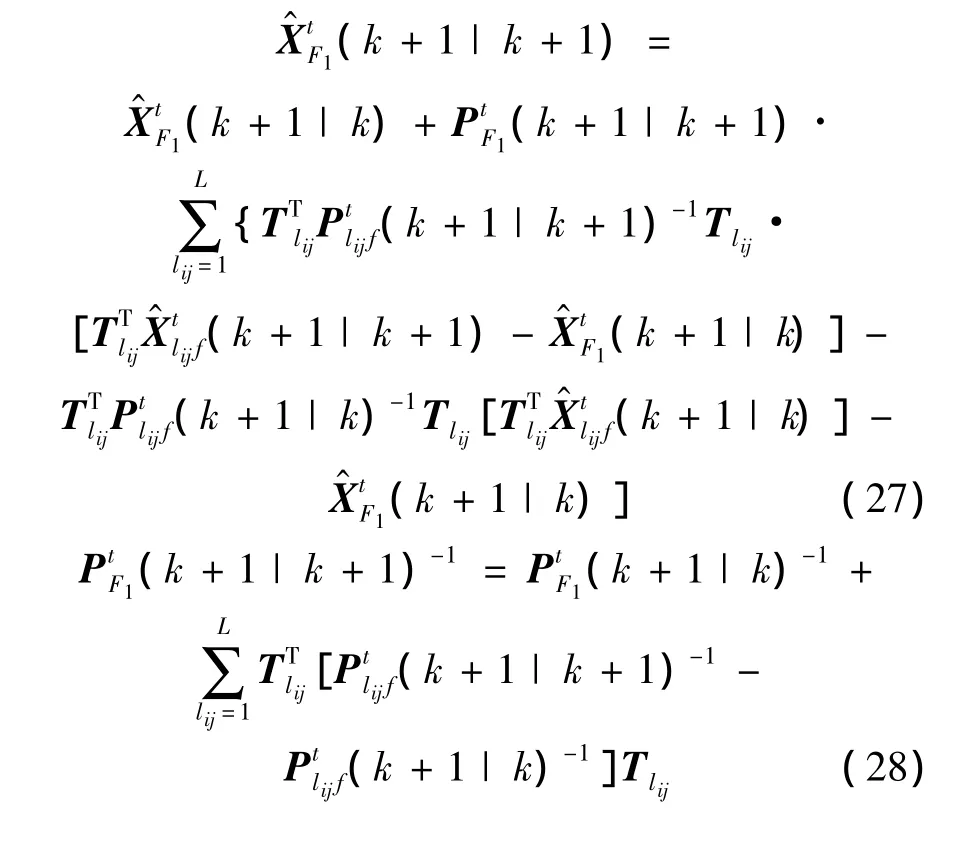
2.3 多目标系统误差估计信息融合估计
第一级反馈融合估计阶段有效地反馈融合了各组合传感器估计信息,获得了对应目标t的第一级融合中心的系统状态估计)和估计协方差,目的是融合利用传感器信息以提高各局部组合节点的状态估计精度.
但显然上述第一级反馈融合估计阶段并未利用各目标信息,而系统状态估计均含有使用目标t的跟踪信息对各传感器系统误差进行估计的信息维,因而可通过构建第二级融合结构,融合利用各目标第一级系统状态估计中传感器系统误差信息,形成对各传感器系统误差的最终融合估计,定义为由于第一级输出融合结果包含对不同目标状态与各传感器系统误差,因而同样可定义第二级融合全局状态估计向量与第二级融合全局状态估计向量)之间的关系为
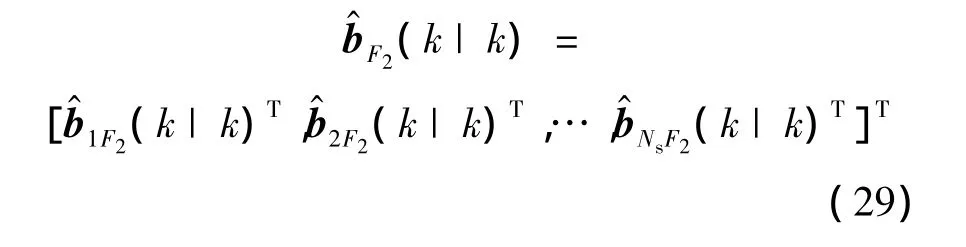
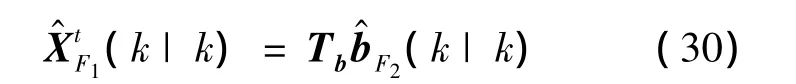
式中,Tb为第二级融合状态空间转移矩阵,也即表示第二级融合全局状态向量到第一级融合状态向量的空间映射关系,具体为
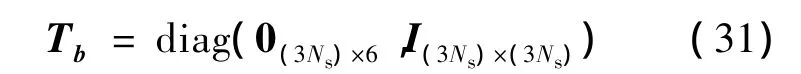
这样,不难推导,第一级融合结果到第二级融合全局状态估计的融合表达式为
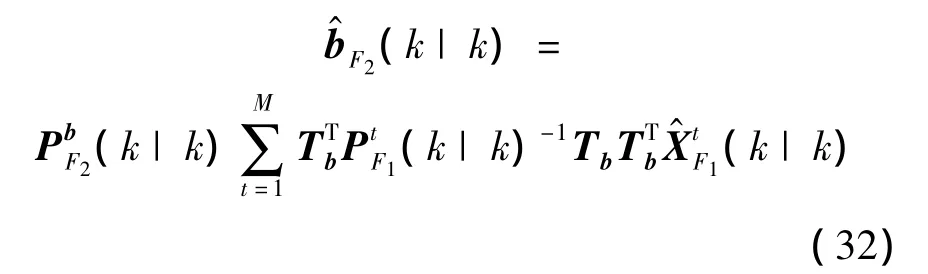
式中

多传感器多目标系统误差融合估计算法的两级融合结构原理框图如图1所示,第一级融合对多传感器组合估计信息进行融合并反馈,而第二级融合对第一级融合输出的估计结果,也即多目标对传感器系统误差估计结果进行融合,从而获得多传感器系统误差的最终融合估计.
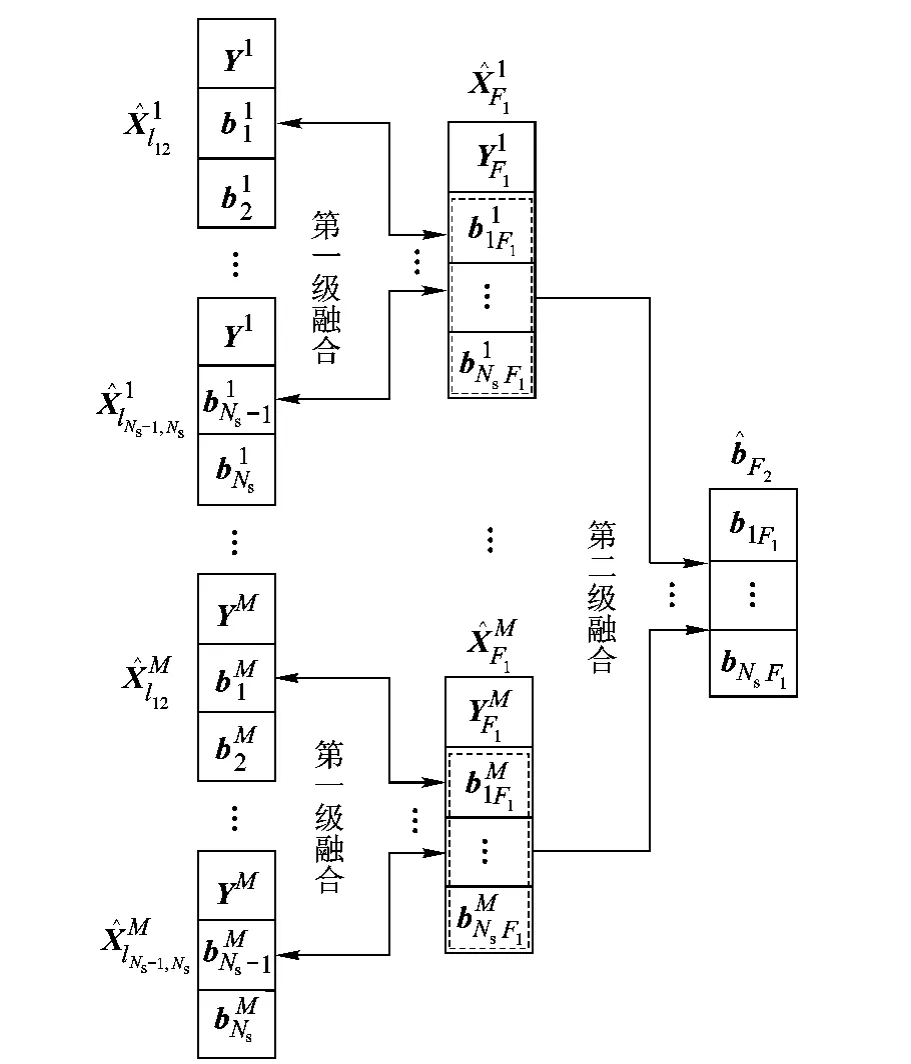
图1 两级融合结构框图
3 仿真验证与分析
采用蒙特卡洛方法,对本文提出的融合估计算法、单一目标的扩维滤波估计算法及文献[10-11]所提出的EX误差估计方法的有效性进行仿真比较、验证和分析.仿真时长设置为1000 s,次数为30次,设定利用3部在空间分布的三坐标探测传感器对公共探测区域中3个呈编队匀速运动的目标进行组网探测.
假设3部传感器的笛卡尔坐标分别为(0 km,0 km,0 km),(185.2 km,0 km,0 km)和(285.2 km,0 km,0 km),测距离、测方位和测俯仰分别具有服从高斯分布的白噪声,且精度分别为50m,0.3°(0.005236 rad),0.1°(0.001745 rad);3 部传感器的距离、方位和俯仰测量系统误差分别设置为1500m,0.008727 rad 和0.008727 rad.
3个编队运动目标的初始状态为

仿真结果如表1、图2~图7所示.表1显示了采用本文算法、扩维算法对各传感器以及EX算法对传感器1、传感器2系统误差最终的均方根误差估计结果,而图2~图7分别给出了算法对传感器1及传感器2各测距、测方位角及测俯仰角系统误差实时估计的均方根误差曲线.

表1 系统误差估计均方差(RSME)
从表1中不难看出,在3种算法中,融合估计算法所获得的估计性能最佳,其中各传感器的系统误差估计精度都很大程度地高于其它2种算法,其性能大约比扩维算法提高了30% ~40%,这是由于融合算法建立了目标状态和系统误差的两级融合估计结构,从而在估计中更为充分地利用了多传感器多目标信息;扩维算法虽然基于多部传感器量测对系统误差进行集中式估计,但并没有融合利用多目标的估计信息,从而使得其估计性能低于本文的融合估计算法;而由于EX算法仅能利用2个传感器量测进行系统误差估计,且该算法不输出对目标状态的估计结果,不能基于多目标状态估计利用多传感器组合估计信息进行融合估计,因而表1显示该算法的系统误差估计精度最差.
此外,仿真结果显示融合估计算法对3部传感器系统误差的估计效果也各不相同,其对传感器3的距离测量系统误差估计性能要优于传感器2,对传感器2的距离测量系统误差估计精度又要好于传感器1,而对角度测量系统误差的估计效果则相反.通过仿真发现,当目标航迹出现在x轴以上时又会呈现出与上面完全相反的规律.因此,这说明目标与传感器之间的相对空间位置关系对相应传感器系统误差的估计性能产生了影响,而由于仿真中采用编队匀速运动目标,其运动形式较为单一、目标分布相对集中且和各传感器之间的相对位置关系相当固定,因而各传感器系统误差估计精度差异较为明显.但在实际应用中,当所选取的各目标航迹在空间中分散分布时,算法对各传感器系统误差的估计精度则能够保持相当.
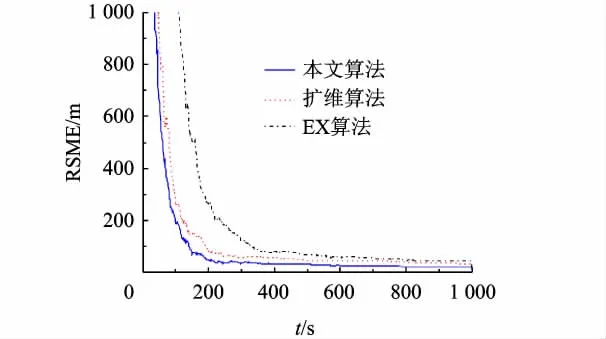
图2 距离测量系统误差估计均方差(传感器1)
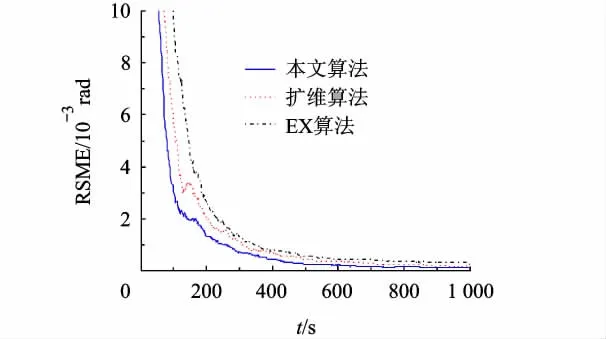
图3 方位测量系统误差估计均方差(传感器1)
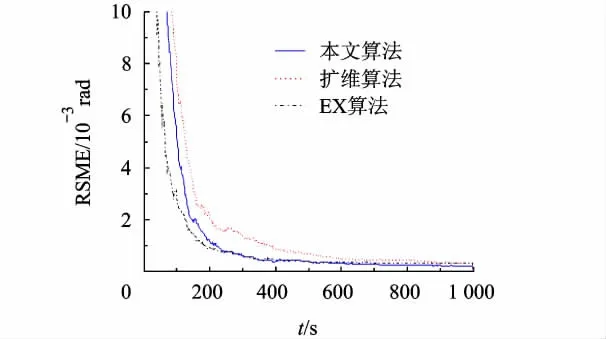
图4 俯仰测量系统误差估计均方差(传感器1)
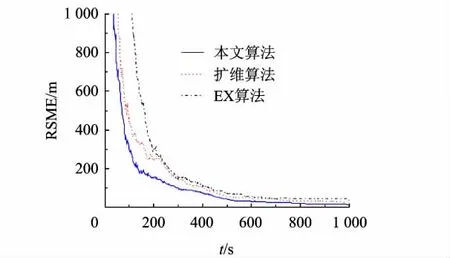
图5 距离测量系统误差估计均方差(传感器2)
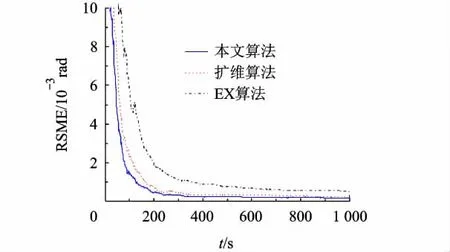
图6 方位测量系统误差估计均方差(传感器2)
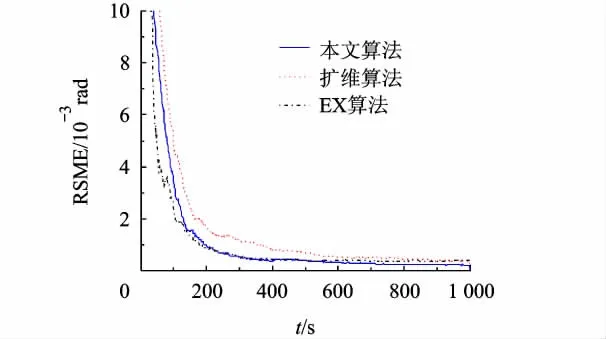
图7 俯仰测量系统误差估计均方差(传感器2)
从对仿真结果图2~图7的分析可以得出,3种系统误差估计算法中,在对测距及测方位角系统误差估计上,融合估计算法具有最快的收敛速度,而在测俯仰角系统误差估计中,其亦能够较快地收敛,且整个仿真中融合估计算法对各传感器系统误差均具有最高的估计性能;而扩维算法由于未能够利用多目标信息,性能稍差于本文算法;EX算法由于未能利用多传感器进行融合估计,性能显示为最差.综上所述,本文提出的融合估计算法能够基于多传感器多目标信息和融合估计结构,对传感器系统误差进行精确有效的实时估计,相较其它算法具有一定的性能优势.
4 结论
本文研究并提出了一种多传感器多目标系统误差的实时融合估计算法,该算法通过构建两级融合结构,能够融合利用多传感器多目标探测信息,实现传感器系统误差的实时组网融合估计.
另外,通过构建不同的状态空间转移矩阵Tlij,本文算法还可实现多异类传感器系统误差的融合估计.
References)
[1]何友,王国宏,陆大金,等.多传感器信息融合及应用[M].2版.北京:电子工业出版社,2007:1-12 He You,Wang Guohong,Lu Dajin,et al.Multisensor information fusion with applications[M].2nd ed.Beijing:Publishing House of Electronics Industry,2007:1 -12(in Chinese)
[2]何友,修建娟,张晶炜,等.雷达数据处理及应用[M].2版.北京:电子工业出版社,2009:274-288 He You,Xiu Jianjuan,Zhang Jingwei,et al.Sensor data processing with applications[M].2nd ed.Beijing:Publishing House of Electronics Industry,2009:274 -288(in Chinese)
[3]董云龙.雷达组网系统中的误差配准技术研究[D].烟台:海军航空工程学院电子信息工程系,2007 Dong Yunlong.Study on sensor registration for radar networking[D].Yantai:Dept of Electronics and Information Engineering,Naval Aeronautical and Astronautical University,2007(in Chinese)
[4] Li Zhenhua,Chen Siyue,Leung Henry.Joint data association,registration,and fusion using EM-KF[J].IEEE Transactions on Aerospace and Electronic Systems,2010,46(2):496 -507
[5] Lian F,Han C,Liu W,et al.Joint spatial registration and multitarget tracking using an extended probability hypothesis density filter[J].IETRadar Sonar Navig,2011,5(4):441 -448
[6]吴泽民,任姝婕,刘熹.雷达系统误差协同配准算法研究[J].兵工学报,2008,29(10):1192 -1196 Wu Zemin,Ren Shujie,Liu Xi.Research oncollaborative registration algorithm for radar system error[J].Acta Armamentarii,2008,29(10):1192 -1196(in Chinese)
[7] Okello N N,Pulford GW.Simultaneous registration and tracking for multiple radars with cluttered measurements[C]//Proceedings of 8th IEEE Signal Processing Workshop on Statistical Signal and Array Processing.Corfu:IEEE Press,1996:60 - 63
[8] Nabaa N,Bishop R H.Solution to amultisensor tracking problem with sensor registration errors[J].IEEE Trans on Aerospace and Electronic Systems,1999,35(1):354 -363
[9] Friedland B.Treatment of bias in recursive filtering[J].IEEE Trans on Automatic Control,1969,AC-14:359 -367
[10] Ignagni M B.An alternate derivation and extension of Friedland’s two-stage Kalman estimator[J].IEEE Trans on Automatic Control,198l,AC-26:746-750
[11] Lin X,Kirubarajan T,Bar-Shalom Y.Exact multisensordynamic bias estimation with local tracks[J].IEEE Trans on Aerospace and Electronic Systems,2004,40(2):576 - 590
[12] Lin X,Bar-Shalom Y.Multisensor target tracking performance with bias compensation[J].IEEE Trans.on Aerospace and E-lectronic Systems,2006,42(3):1139 -1149
[13]何友,熊伟.带反馈分布式不同维传感器状态估计技术[J].宇航学报,2003,24(6):574 -578 He You,XiongWei.State estimation techniques for radars with different observation dimension in one distributed data fusion system with feedback information[J].Journal of Astronautics,2003,24(6):574 -578(in Chinese)
(编 辑:文丽芳)
Multi-sensormulti-target systematic bias fusion estimation algorithm
Song Qiang
(Naval Academy of Armament,Beijing 100036,China)
Xiong Wei He You
(Research Institute of Information Fusion,Naval Aeronautical and Astronautical University,Yantai264001,China)
To solve the problem of sensor systematic bias estimation in sensor network,a systematic bias fusion estimation algorithm was presented based on multi-sensor multi-target information.To solve the forenamed problem,the algorithm was constituted a two layer fusion structure.In order to improve the precision of corresponding combination estimation,the first layer fuses the multi-sensor combination state estimation information with feedback,so the estimation precision of systematic bias can also be improved.While,the second layer fuses the multi-target systematic bias estimation information in order to further improve the estimation precision.The monte-carlo simulation result shows that the algorithm can make sufficient use of the multi-sensor multi-target information with fusion structure,and achieve an exact and real-time estimation of the multi-sensor systematic bias.
systematic bias;sensor network;bias registration;information fusion
TP 953;TN 957
A
1001-5965(2012)06-0835-07
2011-05-06;网络出版时间:2012-06-15 15:43
www.cnki.net/kcms/detail/11.2625.V.20120615.1543.017.htm l
国家自然科学基金资助项目(60801049);全国优秀博士学位论文作者专项资金资助项目(200443)
宋 强(1983-),男,江西新建人,工程师,songqiang8@sina.com.
