空间色噪声下信号频域检测方法性能分析
2012-03-15黄建国焦亚萌
王 静 黄建国 焦亚萌
(西北工业大学 航海学院,西安 710072)
空间色噪声下信号频域检测方法性能分析
王 静 黄建国 焦亚萌
(西北工业大学 航海学院,西安 710072)
水下小孔径阵列的应用环境是色噪声环境,针对超增益波束形成方法在色噪声环境下噪声协方差矩阵估计偏差使阵列空间增益不能达到最大的问题,提出了一种频域超增益波束形成方法(FSD,Super-Directive beam forming in Frequency domain),该方法将宽带接收数据分成多个子带,在每个子带内分别估计噪声协方差矩阵,降低了噪声协方差矩阵的估计偏差,并使用估计得到的噪声协方差矩阵对接收数据解相关.最后使用空间谱检测器检测微弱目标信号.实测噪声数据的仿真结果表明,空间有色噪声环境中FSD方法的检测性能优于传统的时域超增益波束形成方法(TSD,Super-Directive beamforming in Time domain)2 dB,优于频域最小方差无畸变响应(FMVDR,Minimum Variance Distortionless Response in Frequency domain)波束形成方法2 dB.
色噪声;频域;检测;超增益
为了实现对微弱信号的检测,阵列信号处理往往要求获得时间上和空间上的最大增益.时间处理的增益通过噪声抵消、时间预白化等实现,对于水下复杂噪声环境,如果噪声带宽与目标辐射信号带宽重合,这类方法实现难度很大.被动系统中,利用信号和噪声的空域特性的差别,通过阵列接收波束形成,抑制噪声以提高阵元接收端信噪比.提高空域增益的有效方法就是增大阵列孔径,但对于实际应用环境而言,增大阵列孔径要受工作尺度制约,所以往往不现实,因此研究基于小孔径阵列的阵列信号处理方法尤为重要.小孔径阵列是阵元间距远小于半波长的阵列.研究表明,在各向同性均匀噪声场下,当阵元间距-波长比接近于0时,阵增益不趋向1,而是表现出超增益现象[1-3].超增益波束形成方法(SDB,Super-Directive Beam forming)的原理是利用噪声协方差矩阵对阵列接收噪声数据匹配滤波,使基阵增益达到最大,从而提高阵列在低信噪比下的检测概率,因此噪声协方差矩阵的估计至关重要.在实际工作条件下,由于噪声背景的时变性,估计噪声协方差矩阵使用的快拍数有限,造成估计的噪声协方差矩阵偏差较大.
目前常用的噪声协方差矩阵估计方法是极大似然方法(ML,Maximum Likelihood)[4]、归一化采样协方差矩阵估计方法(NSCME,Normalized Sample Covariance Matrix Estimate)[5]和递归似然估计方法(RML,Recursive Maximum Likelihood)[6]等.ML方法直接对阵列接收噪声在时域进行相关运算,原理和计算简单.NSCME方法适用于时域非高斯噪声,将每个阵元上的噪声能量归一化,忽略噪声在不同阵元上的能量差异,仅保留各个阵元接收的噪声序列之间的相关性特征.ML方法和NSCME方法在时域估计噪声协方差矩阵,在阵列接收快拍数小的情况下,其估计偏差很大.RML方法是基于固定点(FP,Fixed Point)估计的迭代ML算法,与NSCME方法相比,该方法使用上一步迭代得到的噪声协方差矩阵的信息将每个阵元上的噪声能量归一化,因此RML方法计算量很大.其他的方法还有最小均方误差(MMSE,Minimum Mean Square Error)[7]和最大后验概率(MAP,Maximum A Posteriori)[7]方法,MMSE和MAP方法是基于贝叶斯准则的估计方法,需要噪声协方差矩阵分布的先验信息,这类信息在实际应用中很难精确获得.
为了实现空间色噪声背景下的最大阵增益,传统方法采用最小方差无畸变响应(MVDR,Minimum Variance Distortionless Response)波束形成方法[8]进行检测,这种波束形成方法可以根据阵列接收数据自适应优化权值,达到对空间有色噪声解相关的效果,从而提高波束形成的空间增益.但是,由于MVDR对目标方向上的功率的约束,输出信号为无失真响应,使得MVDR波束形成器的检测性能受到了限制.
为此,本文针对小孔径阵列的水下有色噪声环境提出了一种FSD(Super-Directive beam forming in Frequency domain)方法,FSD方法将宽带噪声在每个子带上估计噪声协方差矩阵,充分利用了宽带噪声每根线谱的信息,达到了很好对噪声背景解相关的目的.湖试数据的仿真结果证明了其在低信噪比下检测性能的优越性.
1 阵列信号模型
假设M元阵列t时刻接收的窄带信号矢量可以表示为
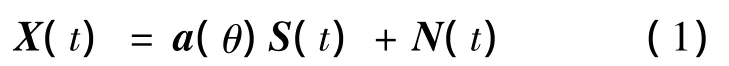
式中,a(θ)表示信号的方向矢量;S(t)=[s1(t),s2(t),…,sM(t)]T为每个阵元接收信号幅值矢量;N(t)=[n1(t),n2(t),…,nM(t)]T为噪声矢量.
式(1)的矩阵形式表示为
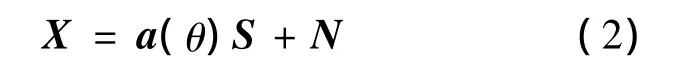
假设噪声和信号是不相关的,则阵列接收数据的相关矩阵为

式中,Rs为有用信号相关矩阵;Rn为背景噪声相关矩阵.
2 波束形成方法
2.1 时域超增益波束形成方法(TSD)
基阵的权向量用 w=[w1,w2,…,wM]T表示,基阵的输出功率P可以表示为
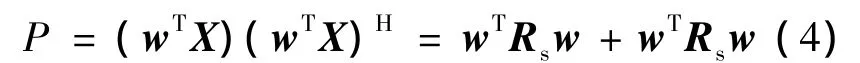
基阵系统的性能由它的空间处理增益来衡量,该基阵系统的增益为
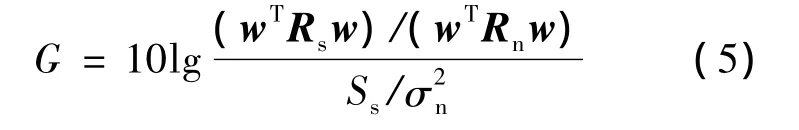
式中,Ss为每个阵元上接收到的信号功率为每个阵元上接收到的噪声功率.
在超增益处理方法中,通过计算找出合适的权系数,使基阵系统的增益达到最大.对式(5)中权系数求导,使d G/d w=0,计算超增益加权系数可得
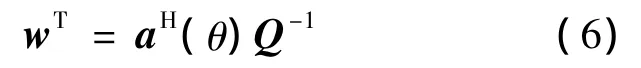
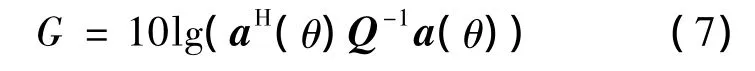
由以上的推导可以看出,超增益方法中使用噪声协方差矩阵对有色噪声背景起到了空域匹配滤波的作用,因而能使基阵的增益达到最大.在超增益算法中噪声协方差矩阵的估计对方法性能起到决定性的作用.
现有常用的噪声协方差矩阵的估计方法是高斯背景下的ML估计方法
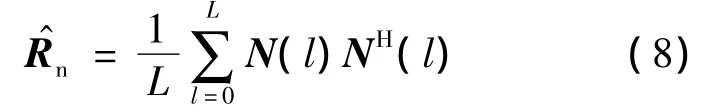
式中,N(l)表示采样得到的噪声序列;L为采样序列长度.将式(8)估计得到的噪声协方差矩阵代入超增益波束形成器,得到TSD(Super-Directive beam forming in Time domain)波束形成器的空间谱输出
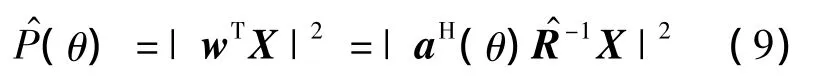
在实际背景下,噪声是时变的宽带噪声,由于ML估计方法仅使用噪声的时域信息,噪声协方差矩阵估计的偏差随快拍数的减小而变大.
2.2 最小方差无畸变响应波束形成方法
MVDR算法中,阵列波束输出的加权系数为[8]
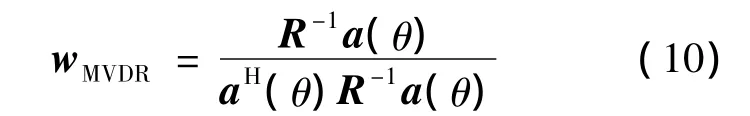
阵列输出功率为[8]
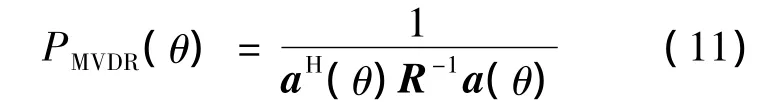
阵增益为[9]
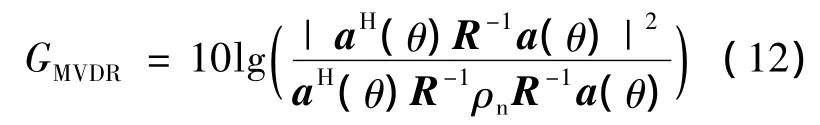
式中ρn表示归一化噪声协方差矩阵.
在MVDR波束形成算法中,采用了阵列接收信号的协方差矩阵求逆,因此能对输入数据解相关,但由于其采用了全部阵列接收信号,包含有用信号和噪声信号,因此解相关的效果损失了一部分的信号能量.在MVDR空间谱输出表达式中,分母表示阵列接收数据在除波束扫描方向θ以外方向上的能量投影,当θ方位存在信号时,分母达到极小值点,空间谱输出出现谱峰,因此可采用MVDR波束形成算法进行空间谱能量检测.
对比式(7)和式(12),超增益波束形成算法和MVDR波束形成算法的阵增益表达形式相近,超增益波束形成算法阵增益只和噪声背景有关,而MVDR波束形成算法和阵列接收数据有关.
3 频域超增益波束形成方法(FSD)
由上小节的推导和分析得出,噪声协方差矩阵的估计在超增益波束形成算法中起着至关重要的作用.由于阵列接收的噪声为宽带有色噪声,在一定的时间范围内,工作频带内噪声在每一频点上的能量基本稳定,为了充分利用噪声在每一频点上的信息,本文提出FSD方法.FSD方法在每个子带内估计噪声协方差矩阵,并将估计得到的噪声协方差矩阵对子带内的阵列接收数据匹配滤波,得到阵列输出,最后将每个子带处理的结果非相干叠加.
接收阵的工作频带为宽带时,阵列接收数据按每L点分K段采样,每段采样数据点数为L/K.对每段采样数据作FFT,根据实际有效工作频段确定相应的J根线谱,每个有效子带频率fi(1≤j≤J)同时得到K个频域采样数据,相应的阵列频域输出模型为
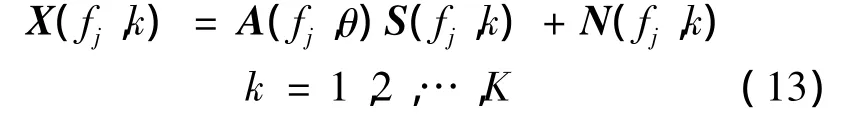
在实际应用中,对一定的子带频率fj,估计阵列接收数据的协方差矩阵
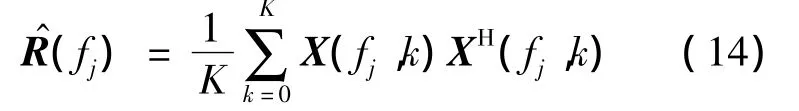
式(14)为阵列接收数据在子带频率fj上的频域估计值.当阵列接收数据仅含有噪声时,估计得到的矩阵为频域噪声协方差矩阵.将式(14)估计的噪声协方差矩阵代入超增益波束形成器,得到子带频率fj上的空间谱输出
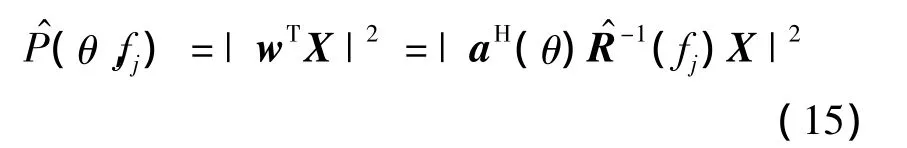
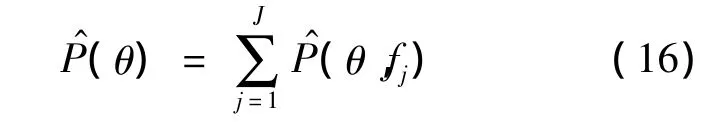
对比式(9)和式(15),TSD方法将阵列接收的宽带数据不分频带地在时域进行波束形成,FSD方法将宽带数据在每个子频带上进行波束形成,再将每个子带的结果做加权平均.FSD方法估计噪声在每个子带内的协方差矩阵信息,频域估计的噪声协方差矩阵充分使用了工作频带内每一频点的噪声信息,因此能更加精确地对阵列接收数据解相关,能获得更大的阵列增益,其检测性能也优于TSD方法.
4 仿真和实验结果
为了验证频域超增益波束形成方法的有效性,采用湖试实测噪声数据做了仿真研究.
目标方位未知时,对基阵接收信号进行波束形成,通过密集波束扫描实现目标的空间谱检测.空间谱检测实验步骤如下:
1)对实测噪声数据多次进行波束形成,学习噪声空间角谱.
2)根据系统预先设定的虚警概率,并考虑噪声空间角谱峰值设定相应的能量检测门限.
3)对以一定信噪比合成的数据按照相应的波束形成方法做空间角谱.
4)将合成数据空间角谱的峰值和检测门限比较,若大于门限值,判断有目标,否则判无目标.
当阵列接收数据为宽带数据时,常采用频域波束形成方法,将宽带数据首先做FFT变换,将宽带数据分成相应的多个子带,在每个子带上分别进行波束形成,并将各个子带的结果综合得到最终频域波束形成输出结果.对于FSD方法,分别学习各个子带上的噪声协方差矩阵,采用各个子带的噪声协方差矩阵对对应子带的阵列接收数据解相关,并计算得到FSD方法的空间角谱.由于FSD方法在阵列的不同方位能取得的阵增益不同,在端射方向取得的阵增益最大,正横方向最小,因此,理论上FSD方法在端射方向的检测性能优于正横方向的检测性能.
本文设计了实验研究,首先研究噪声背景特性,其次研究理论和实测噪声环境下FSD方法在不同束控方向的阵增益,并研究了FSD方法在不同目标来向情况下的检测性能,验证了“FSD方法在端射方向的检测性能优于正横方向的检测性能”的推测,最后,将FSD方法和FMVDR,TSD方法的检测性能做了比较.
实验中使用的阵列为8元均匀线列阵,阵元间距为工作频带中心频率波长的0.1倍,属于小孔径阵列,系统的归一化工作频带为0.2~0.4.设定的虚警概率Pf=0.05,每次检测所使用的数据长度为500快拍,仿真结果为100次蒙特-卡洛仿真结果的平均.
仿真1图1表示实测噪声的功率谱和不同阵元间距阵元之间接收噪声序列的相关系数.从图1的仿真结果得出,噪声的频带为0.2~0.4,工作频带内噪声功率谱起伏不大,表明接收的宽带噪声在工作频段内为时域白噪声.各个阵元和1号阵元接收的噪声序列之间的相关系数在-0.3778~1之间,其中5~7号阵元与1号阵元接收噪声序列的相关系数为负值,表示信号负相关,其绝对值的大小表示相关程度,8号阵元与1号阵元接收噪声序列之间的相关系数为0.148,比2~7号阵元与1号阵元接收噪声序列之间的相关系数的绝对值小,表示8号阵元与1号阵元接收噪声的相关性最小.从图1可以看出实测的噪声数据在各个阵元之间的相关性很强,为空间相关性强的宽带有色噪声.
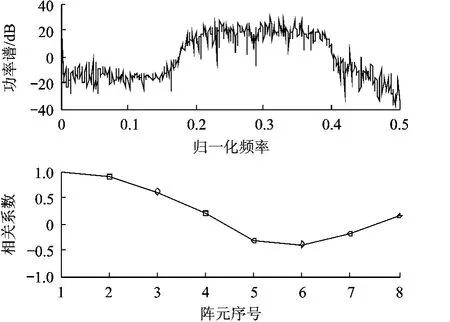
图1 实测噪声频谱与相关系数曲线
仿真2图2表示在仿真1中的实测噪声背景和理想噪声背景[3]下FSD波束形成方法的阵增益与束控方向的关系曲线,其中0°表示正横方向.可以看出,在实测和理想的噪声背景下,FSD方法的阵增益在正横方向达到最小.实测噪声背景下FSD的阵增益在±50°方向左右达到最大,端射方向的增益略微下降,这与超增益波束形成方法在阵增益在各向同性均匀噪声场中正横方向最小,端射方向最大[1]的结论稍不同,这是由于实际的空间有色噪声背景不是理想的各向同性均匀噪声场,而是具有一定空间相关性的有色噪声场.FSD方法在±50°方向左右的阵增益大于正横方向约 2.7 dB.
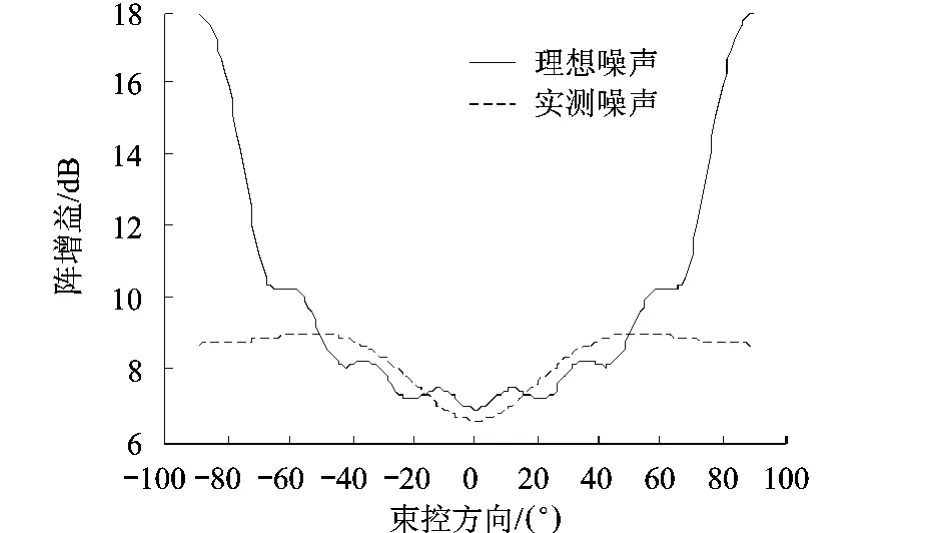
图2 超增益波束形成方法阵增益和束控方向的关系
从图2的结果可以推测得到以下结论:目标来向不同的情况下,FSD波束形成方法的检测能力不同,正横方向上的检测能力最差.
仿真3图3表示在仿真1中的实测噪声背景下,目标来向改变的情况下FSD检测概率随信噪比的变化曲线.其中信号为仿真产生的窄带信号,信号的中心频率与噪声带宽的中心频率重合.可以看出检测概率达到90%时,目标来向为30°时的检测性能优于目标来向为0°时的检测性能,两者相差约1~2 dB.对比图2的仿真结果,当束控方向对准30°和0°时,FSD在两者之间的阵增益相差约1~2 dB,图3的检测结果与图2的仿真结果吻合.
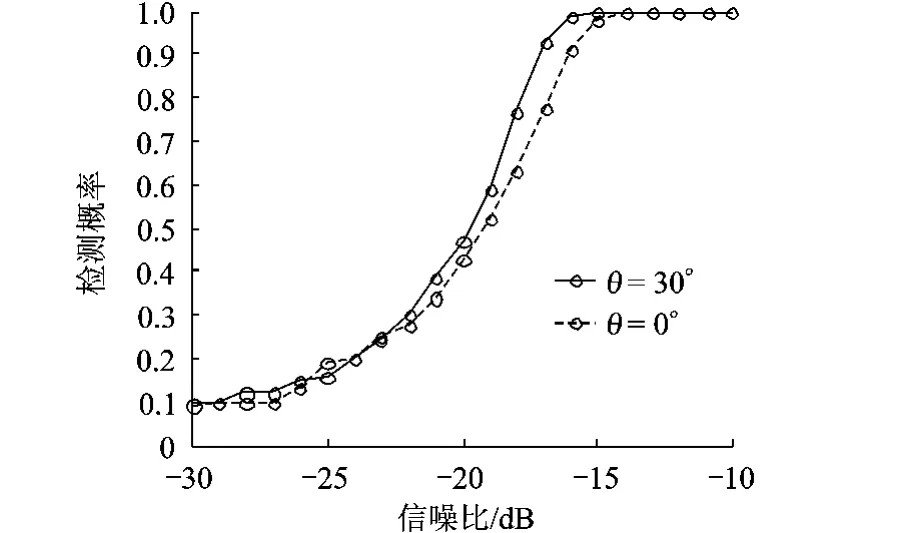
图3 不同目标来向FSD检测概率随信噪比变化曲线
仿真4图4表示FSD和FMVDR波束形成方法检测概率随信噪比变化的曲线.噪声为仿真1中的宽带噪声,目标辐射信号为和噪声同频带的宽带信号,阵元接收数据是两者以一定的信噪比合成的宽带信号.每次检测所使用的数据长度为500快拍,将数据分成10段进行采样,数据重叠率为0.5,其中FMVDR波束形成器为频域宽带波束形成器[8],FSD和FMVDR波束形成方法的频域子带个数相同.从湖试数据结果来看,FSD方法的检测性能远好于FMVDR波束形成方法的检测性能.在达到90%检测概率的情况下,FSD方法的检测性能优于FMVDR波束形成方法约2 dB.影响FSD方法检测性能优于FMVDR方法的因素有以下几点:①宽带信号和噪声背景的时频域特性差异很大,FMVDR方法计算权系数时信号成分起主要作用,对信号的白化程度很大,降低了输出端信噪比;②子带分解个数的影响,不同的子带分解个数方法的检测性能也不同;③信号和噪声平稳性的影响.FSD方法在估计噪声协方差矩阵时采用较长时间序列,估计精度比较高.FMVDR方法估计数据协方差矩阵采用的是短时间序列.
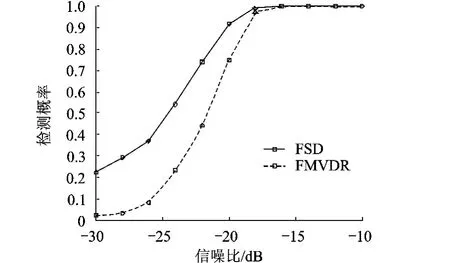
图4 FSD和FMVDR波束形成方法检测概率随信噪比变化曲线
仿真5图5表示FSD和TSD方法检测概率随信噪比变化的曲线.噪声为仿真1中的宽带噪声,目标辐射信号为和噪声同频带的宽带信号,阵元接收数据是两者以一定的信噪比合成的宽带信号.其中每次检测所使用的数据长度为500快拍,FSD和TSD方法估计噪声协方差矩阵所使用的噪声快拍数都为200,为短时间段的噪声数据.TSD方法中对宽带数据预先进行了滤波处理,保证了TSD方法的工作带宽和FSD方法重合.从仿真结果看出,FSD的检测性能优于TSD方法.在达到90%检测概率的情况下,FSD方法优于TSD方法约2 dB.FSD方法检测性能优于TSD方法主要是因为FSD方法在频域估计噪声协方差矩阵,充分利用了宽带数据每一频点上的数据信息,对噪声协方差矩阵的估计精度高于TSD方法,因而对噪声解相关的效果好于TSD方法.

图5 FSD和TSD方法检测概率随信噪比变化曲线
从仿真4和仿真5结果可知,本文所提FSD方法具有以下优点:
1)检测性能优于FMVDR波束形成方法;
2)在估计噪声协方差矩阵的数据长度相同的情况下,检测性能优于TSD方法.
5 结论
本文提出了频域超增益波束形成方法(FSD),仿真结果表明FSD具有以下优点:
1)在达到90%检测概率的情况下,FSD方法的检测性能优于TSD方法约2 dB.与其他波束形成方法的检测性能相比较,在达到90%检测概率的情况下,FSD方法的检测性能优于FMVDR波束形成方法约2 dB.
2)提出的FSD方法仅需要对估计的噪声协方差矩阵一次求逆,计算量小,适合工程应用.
References)
[1] Uzkov A I.An approach to the problem of optimum directive antenna design[J].Compt Rend Acad Sci U R SS,1946
[2] Yan Shefeng,Ma Yuanliang.Robust supergain beamforming for circular array via second-order cone programming[J].Applied Acoustics,2005,66(9):1018 -1032
[3]鄢社锋,马远良.圆环形声基阵低频超增益性能研究[J].西北工业大学学报,2002,20(1):79 -82 Yan Shefeng,Ma Yuanliang.A circular hydrophone array for supergain in low frequency[J].Journal of Northwestern Polytechnical University,2002,20(1):79 -82(in Chinese)
[4] ShuaiXiaofei,Kong Lingjiang,Yang Jianyu.Performance analysis of GLRT-based adaptive detector for distributed targets in compound-Gaussian clutter[J].Signal Processing,2010,90(1):16-23
[5] Bon N,Khenchaf A,Garello R.GLRT subspace detection for range and doppler distributed targets[J].IEEE Transactions on Aerospace and Electronic Systems,2008,44(2):678 -695
[6] Pascal F,Chitour Y,Forster P,et al.Covariance structure maximum-likelihood estimates in compound Gaussian noise:existence and algorithm analysis[J].IEEE Transactions on Signal Processing,2008,56(1):34 -48
[7] Bandiera F,Besson O,Ricci G.Knowledge-aided covariance matrix estimation and adaptive detection in compound-Gaussian noise[J].IEEE Transactions on Signal Processing,2010,58(10):5391-5396
[8]游鸿,黄建国,史文涛.基于宽带分裂阵列的水下远程被动多目标检测与定向[J].声学学报,2009,34(6):527 -532 You Hong,Huang Jianguo,ShiWentao.Long-distance underwater passive multi-target detection and direction finding based on the wideb and split array [J].Acta Acustica,2009,34(6):527-532(in Chinese)
[9]Van Trees Harry L.最优阵列处理技术[M].汤俊译.清华大学出版社,2008:327 Van Trees.Harry L.Optimum array processing[M].Translated by Tang Jun.Beijing:Tsinghua University Press,2008:327(in Chinese)
(编 辑:娄 嘉)
Performance analysis for frequency domain detection method in spatial color noise background
Wang Jing Huang Jianguo Jiao Yameng
(College of Marine Engineering,Northwestern Polytechnical University,Xi’an 710072,China)
Underwater noise environment of small aperture array is spatial color noise background.A super-directive beamforming in frequency domain(FSD)method was proposed to solve the problem that the array gain of super-directive beamforming cannot reach maximum when there exists error in the estimated noise matrix under color noise background.Thewideb and
data were divided intomany subbands,and noise covariance matrix in each sub band was estimated,which reduces the error of estimated noise matrix.Estimated noise covariance matrix was used to de-correlate the received data.At last,spatial spectrum detector was employed to detect weak signal.Experimental results show that the detection performance of FSD is better than super-directive beam forming in time domain(TSD)and minimum variance distortionless response in frequency domain(FMVDR)of 2 dB and 2 dB respectively.
color noise;frequency domain;detection;super-directive
TN 911.7
A
1001-5965(2012)06-0783-05
2011-03-17;网络出版时间:2012-06-15 15:44
www.cnki.net/kcms/detail/11.2625.V.20120615.1544.032.htm l
国家重点实验室基金资助项目(9140C2304080607)
王 静(1986-),女,河南商丘人,博士生,wangjing0407 j039@yahoo.com.cn.
