基于C42+分子的TÄt2系统的频率约化矩阵计算

王仙枝，冯胜奇



基于C42+分子的Ä2系统的频率约化矩阵计算

王仙枝1，*冯胜奇2

( 1. 韩山师范学院数学与信息技术系，广东，潮州 521041；2. 韩山师范学院物理与电子工程系，广东，潮州 521041)

利用群论和微扰论计算了C42+分子的Ä2系统在其4个具有3v对称性势阱中的频率约化矩阵。文中首先探讨了任意的杨-泰勒系统的频率约化矩阵及其计算方法，随后借助Mathematica程序求出了Ä2系统在其4个对称性势阱中的频率约化矩阵，最后利用群论进一步分析了系统的振动频率分解与各向异性现象。结果表明，系统的杨-泰勒畸变导致系统的三重简并振动模式2的振动频率发生了分解，而系统的频率分解就意味着系统的各向同性遭到破坏而呈现出各向异性现象。

频率约化矩阵，Mathematica，频率分解，各向异性

在对分子、团簇分子以及晶体等物质的研究中，有关杨-泰勒（Jahn-Teller，以下简写为J-T）效应的研究是一个非常重要的分支，最近20多年来，人们都对J-T效应进行了广泛和深入的研究[1-7]。研究发现，J-T效应对物质的几何构型及其物理与化学性能都有较大的影响。比如C42+、Pu4+、B2H6分子的几何构型就与J-T效应有着极大的关系[1-5]，而钨钛矿和汞锰矿铁磁材料的物理与化学性质也是与J-T效应有不可分割的联系[6-7]。分析与研究指出[8-11]：如果某种对称性系统(链状分子除外)的电子基态是简并的，则这一系统往往是不稳定的，系统的电子态与声子态之间就会发生耦合作用并导致系统发生J-T效应。J-T效应的发生将会导致系统从一个对称性较高的状态畸变到一个对称性较低的状态，通常还伴随有系统的能级分裂、频率分解以及各向异性等现象发生。有多篇文献对具有T对称性的C42+分子的J-T效应、能级分裂及其对称性破缺进行了分析与研究[1-2,8]，但并没有探讨C42+分子在其势能面上的各个势阱中的频率约化矩阵计算以及频率约化矩阵对系统频率分解的影响等相关问题。本文借助群论和微扰论，利用Mathematica方法探讨了具有T对称性的C42+分子的Ä2系统在其4个对称性势阱中的频率约化矩阵计算及其对系统频率分解与各向异性的影响等相关问题。

1 J-T系统的频率约化矩阵

对于一个任意的J-T系统而言，描述系统原子核振动的势能是其简正坐标Q（=1～）的函数(Q)。由于电声耦合作用的缘故系统通常会发生J-T畸变，畸变将导致系统在其势能面上形成多个势阱[10-11]，探讨系统在势阱中的运动特性是研究J-T效应的主要内容之一，但势阱中的系统运动往往是非常复杂的，为此我们通常采用近似方法进行处理，将系统的势能函数(Q)在势阱附近进行泰勒展开，近似到Q的二次项，结果为：

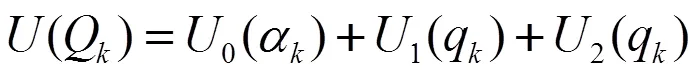
式中的α（=1～）表示系统的势阱位置，而0、1、2分别表示势能函数展开式中的常数项、一次项与二次项，其数学表达式分别为：

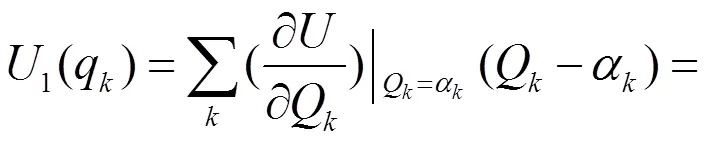
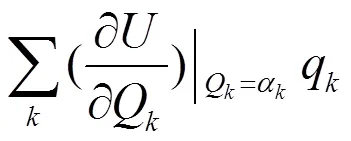
(4)

式中q=Qα（=1~）表示系统离开势阱位置的位移。显然式（1）中的第一项由势阱的具体位置确定，而其余两项则必须作为微扰项来处理。如上所述，系统的电声耦合作用通常会导致系统的势能面发生畸变，畸变的结果就是在系统的势能面上会形成多个对称性程度较低的势阱，这些不同的势阱所对应的势能函数是不一样的。依据微扰论，在势阱附近系统的势能函数可以表示为：

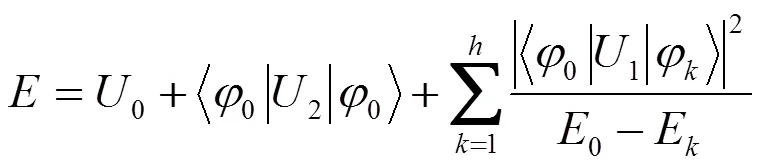
式中0是系统在势阱中的电子基态，而φ（=1,…,）是系统在势阱中的电子激发态，式（5）中仅仅只含有系统位移q的二次方项，而不含有q的一次方项，这是因为系统势能函数在势阱中应该取极小值的缘故。引入矩阵和列向量，式（5）可表示为：

式中上标符号“～”表示转置，而矩阵的矩阵元m（=1,…,）由下式确定：

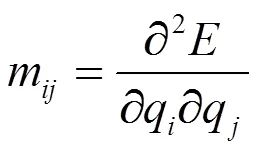
依据物理学原理可知矩阵描述了系统的振动特性，求解矩阵就能够了解系统的固有振动频率等振动特性。一般情况下，矩阵并不是对角化的，但是我们总可以通过一个幺正矩阵将矩阵对角化，也就是说一定存在一个幺正矩阵使得下式成立：

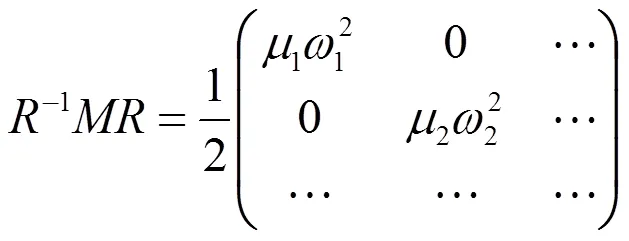
式中ω（=1,2,…）是系统的固有振动频率,而μ为系统的第个振动模式的等效质量，通常称幺正矩阵为系统的频率约化矩阵[11]。

2 C42+分子的TÄt2系统在势阱中的频率约化矩阵计算

2.1 T Ät2系统的对称性势阱及势阱中的电子态

C42+分子的Ä2系统的J-T畸变以及由于J-T畸变而在系统势能面上所形成的势阱分布及势阱特性已有文章进行过探讨[8]，为了便于下面进一步的分析与研究，需要对文献[8]中的结论进行优化。C42+分子的Ä2系统的电声耦合哈密顿量具有如下的形式[8]：

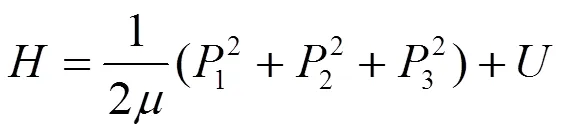
式中的第一项是系统的动能，第二项为系统的势能，其表达式为[8]：

(10)

上式中的12、3是C42+分子的三重简并振动态2的简正坐标，而1、2、3是与之对应的正则动量；、是振动态2的等效质量与等效角频率；1、2、3是系统的等价电子轨道算符；V、V是系统的一次与二次电声耦合系数，它们描述了系统的电子态与振动态之间耦合作用的强弱。用|X>(=1～3)表示系统简并电子基态的三个态矢量，这三个态矢量构成了系统的一个态矢子空间，在这个态矢子空间中，可以将式（10）中的等价电子轨道算符表示为矩阵形式[8]：

(11)

引入如下的幺正平移变换[8]，

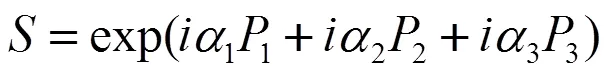
式中的1、2、3是待定物理参量，它们描述了由于电声耦合作用在系统的势能面上所形成的势阱位置。借助幺正平移变换可计算出J-T畸变后的系统在各个势阱中的电子基态与激发态及其能量[8]，结果列于表1中，表1中的符号（,,）是系统电子态|1ñ+|2ñ+|3ñ的缩写形式，系统的基态能量0、激发态能量1以及参数分别为：

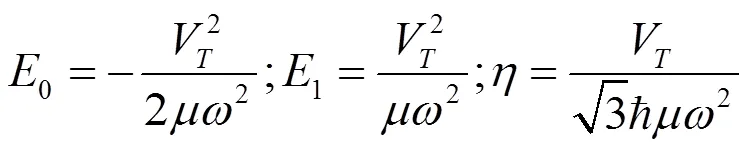
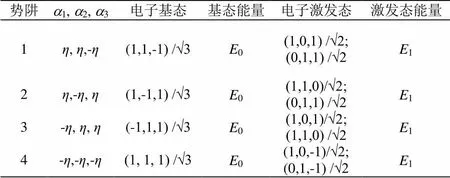
表1 T Ät2系统在各个势阱中的电子基态与电子激发态及其能量

2.2 T Ät2系统在各个势阱中的频率约化矩阵计算

系统的电声耦合作用一定会导致系统发生J-T畸变，畸变结果就是系统的对称性会降低，同时会导致系统的能级分裂、振动频率分解。在探讨系统频率分解的时候就必须要计算系统在势阱中的频率约化矩阵。显然，在不同的势阱中系统的频率约化矩阵是不同的，这是因为在不同的势阱中，系统的电子态是不同的，因而根据式（5）所求得的势能函数就不一样，这就导致在不同的势阱中系统的矩阵就不一样，因而对应的频率约化矩阵也就不一样。下面以Ä2系统在势阱1中为例计算系统的频率约化矩阵,依据式（3）、（4）可求出系统的势能函数1、2分别为：

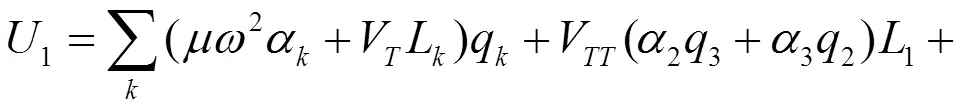
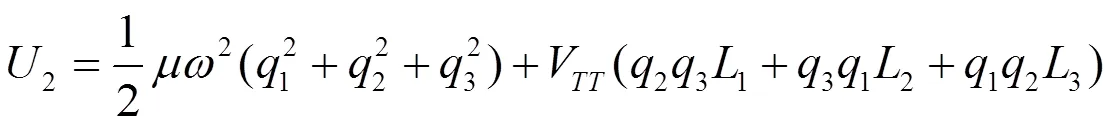
在势阱1中1=，2=，3=-，利用上式以及式（5）就可求出系统在势阱1中的势能函数为：

由此即可求出系统在势阱1中的矩阵，由矩阵就能计算系统在势阱1中的频率约化矩阵，为了简化计算，可借助Mathematica方法，设计一个源程序来计算频率约化矩阵，下面就是这样的一个Mathematica源程序：

ein [A_ ]:=A/Sqrt[A.A]

einvectors [A, n_ ]:=Table[Simplify[ein[A[[i]]]],{i,n}]

Schmidt [A, n_ ]:=Module[{b0,i,j},b0=Table[0,{i,n}, {j,n}];b0[[1]]=A[[1]];Do[b0[[i]]

=Simplify [A[[i]]-Sum[A[[i]].b0[[j]]/(b0[[j]].b0[[j]])

b0[[j]],{j,i-1}]],{i,2,n}];Return[b0]]

Schmidteigenvectors [B, n_ ]:=einvectors [Schmidt [Eigenvectors[B],n],n]

Schmidtsystems [B, n_ ]:={ Eigenvalues [B], Transpose[ schmidteigenvectors [B,n]]}

利用这一源程序和表1中的数据，可求出系统在势阱1中的频率约化矩阵1为：

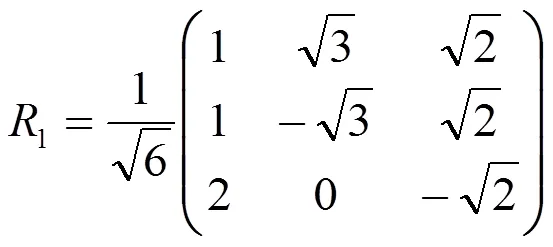
利用类似的方法，同样可计算Ä2系统在系统其余的3个势阱中的频率约化矩阵为：

式中的的R（=2～4）表示系统在其编号为的势阱中的频率约化矩阵。

3 C42+分子的频率分解与各向异性现象

C42+分子的振动自由度是6，在这6个自由度的振动中，并不是所有的振动频率都是互不相同的，因为C42+具有T对称性，因此就会有一些振动具有相同的频率，这些具有相同频率的振动就构成了所谓的简并振动模式。研究表明[8]，C42+分子存在3种不同频率的振动模式，它们分别具有T群下的1、、2对称性，其中振动模式1是非简并的，振动模式是二重简并的，而振动模式2是三重简并的。二重简并的振动模式的存在就意味着在其振动平面上系统具有各向同性，而三重简并的振动模式2的存在则意味着在空间上系统具有各向同性。但是，电声耦合作用将导致C42+分子发生畸变，畸变将导致C42+分子的振动频率由原初的3种增加到畸变后的4种[8]，这就是所谓的系统振动频率分解。我们可以借助前面所求出的系统频率约化矩阵与标度变换并结合微扰论来计算系统的振动频率分解，由于这一计算复杂且冗长，这里不介绍具体的计算过程，仅将计算结果列在下面。计算表明，畸变之后系统的三重简并振动模式2的三个分振动的振动频率1、2、3分别为：

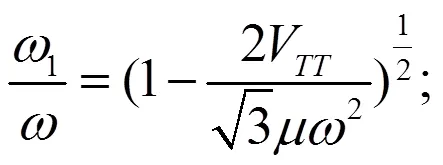
式中是畸变前振动模式2的振动频率。由于畸变后的这三个频率并不相等，这就说明畸变导致简并振动模式2的振动频率发生了分解，畸变后的频率1≠2=3，就意味着频率为1的振动是一种非简并的振动模式，而频率为2=3的这两个振动形成了一种二重简并的振动模式。因此畸变导致系统的三重简并振动模式2从原初的只具有单一频率的振动模式变成了具有两种不同频率的振动模式，也就是说系统的振动频率发生了分解。这与上面利用对称性分析所得到的结论完全一致。进一步的分析表明，畸变后频率为1的振动模式具有3v群下的1对称性，而频率为2=3的这两个振动所形成的二重简并振动模式则具有3v群下的对称性。特别需要指出的是，依据式（18）不难发现：系统在畸变后的三个分振动频率都小于畸变前的振动频率，这就表明畸变后系统的振动基态能量比畸变前的振动基态能量降低了，正是因为这一基态能量的降低就致使系统经过J-T畸变达到了一个更加稳定的状态。

4 结语

文中利用群论和微扰论并借助Mathematica程序计算了具有T对称性的C42+分子的Ä2系统在其4个具有3v对称性势阱中的频率约化矩阵，探讨了系统的频率分解与各向异性现象。计算表明，在系统的4个对称性势阱中其频率约化矩阵是不一样的，但是在这4个势阱中系统的振动频率分解则完全相同，其根本原因就是系统的这4个势阱具有相同的3v对称性。文中的计算与分析进一步地指出，系统的电声耦合作用导致系统发生了J-T畸变，畸变致使C42+分子原初的各向同性遭到破坏而呈现出各向异性特性，同时畸变还导致C42+分子的振动基态能量比畸变之前的振动基态能量降低了，正是这一基态能量的降低致使C42+分子经过J-T畸变达到了一个更加稳定的状态。利用本文的分析与结论，我们还可以进一步探讨系统的许多其它特性，例如分析系统的各向异性对Ham约化因子的影响，探究系统的能级反演分裂等等，这将是我们下一步所要开展的工作。

[1] 汪蓉,朱正和,杨传路. C42+的几何构型和Jahn-Teller效应[J].物理学报, 2001,50(9): 1675-1680.

[2] 冯胜奇, 邱庆春. 具有4h对称性构型的C42+分子的Jahn-Teller效应与能级分裂[J].物理学报, 2011, 60(5): 057106(1-9).

[3] 黄辉,李权.Pu4+的几何构型和Jahn-Teller效应[J].原子与分子物理学报, 2003, 20(7): 409- 412.

[4] 阎世英,马美仲,朱正和. B2H6分子的几何构型[J].物理学报, 2005,54(7):3106-3110.

[5] 冯胜奇, 方海, 邱庆春.具有3h对称性构型的B2H6分子的杨-泰勒效应与能级分裂[J].原子与分子物理学报, 2011,28(2):217-224.

[6] Wu W B, Huang D J, Huang C M, et al. Orbital polarization and Jahn-Teller distortion of strained La0.5Sr0.5MnO3thin films[J]. Magnetism and Magnetic Materials, 2007, 310: 813-815.

[7] Zheng G H, Ma Y Q, Zhu X B, et al. Effects of Cr doping in electron-doped manganites La0.9Te0.1MnO3[J]. Solid State Communications, 2007, 142: 217-222.

[8] 冯胜奇. 具有Td对称性构型的C42+分子的Ä2系统的杨-泰勒效应分析[J].西南大学学报:自然科学版, 2011, 36(2): 39-44.

[9] Bishop D M. Group theory and chemistry [M]. London: Oxford University Press, 1973:151-160.

[10] 冯胜奇, 方海, 邱庆春. 在群论框架下电子三重态与声子耦合的理论研究[J].物理学报, 2011, 60(1): 017105(1-8).

[11] 袁乃荣, 邬鸿彦, 李铮, 等.1uÄgJahn-Teller系统中的频率约化矩阵[J].物理学报, 2000, 49(9): 1769-1777.

Calculation of reduced matrices of vibrational frequencies of theÄ2system for C42+molecules and Mathematica applying

*WANG Xian-zhi1,FENG Sheng-qi2

(1. Department of Math and Information Technology, Hanshan Normal University, Chaozhou, Guangdong 521041, China;2: Department of Physics and Electronic Engineering, Hanshan Normal University, Chaozhou, Guangdong 521041, China)

The reduced matrices of vibrational frequenciesoftheÄ2system for C42+molecules are calculated using group theory, perturbation theory and Mathematica program. Firstly, the reduced matrices of vibrational frequencies of the Jahn-Teller systems and their calculation methods are discussed. Furthermore, the reduced matrices of vibrational frequencies of theÄ2system in the four minima are computed using Mathematica program. Finally, the phonon splitting and anisotropy of the system are further analyzed using group theory. It is found that the Jahn-Teller distortion results in phonon splitting of the triply degenerate vibrational mode2of C42+molecules, and the phonon splitting signifies that the isotropy of the system is destroyed and its anisotropy should appear.

reduced matrices of vibrational frequencies; Mathematica; phonon splitting; anisotropy

1674-8085(2012)03-0021-05

O561.1

A

10.3969/j.issn.1674-8085.2012.03.005

2012-03-07；

2012-04-01

广东省自然科学基金项目(34613)

王仙枝(1973-)，女，湖北浠水人，主要从事计算机教学与应用研究(E-mail:wxz@hstc.edu.cn);

*冯胜奇(1962-)，男，湖北武穴人，副教授，主要从事分子与晶体研究(E-mail:fsq2002@126.com).