广义分裂下的预处理Gauss-Seidel迭代法收敛性的讨论

2012-03-14张仕光

井冈山大学学报(自然科学版) 2012年3期

周婷，张仕光

*周婷，张仕光

(衡水学院数学与计算机学院，河北，衡水 053000)

运用Gauss-Seidel迭代法解线性方程组，讨论了在一类预条件矩阵下的Gauss-Seidel迭代法的收敛性。在更广义的分裂条件下，对预条件Gauss-Seidel迭代法和相应的Gauss-Seidel迭代法的收敛性进行了比较，得到了比较定理。最后给出数值例子验证了所得到的主要结论。

预条件；-矩阵；-矩阵；Gauss-Seidel迭代法

考虑线性方程组

， (1)

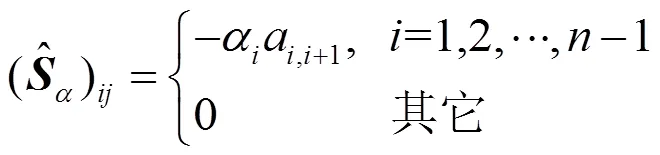
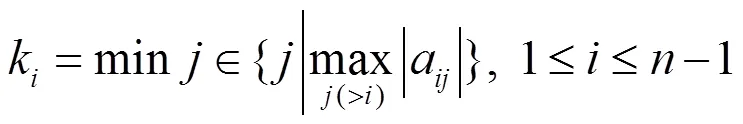
1 预备知识

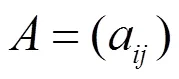
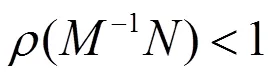
引理 1[7]设是一个-矩阵，那么下面几个命题等价：

(1)是非奇异-矩阵；

(3)的所有主子式都是正的.

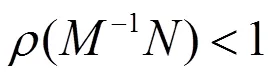
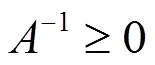
2 主要结果

则预条件Gauss-Seidel迭代法的迭代矩阵为

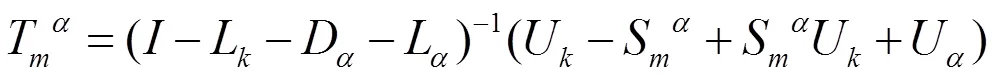
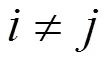
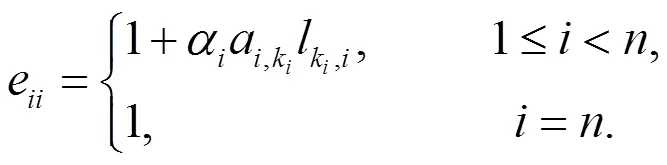
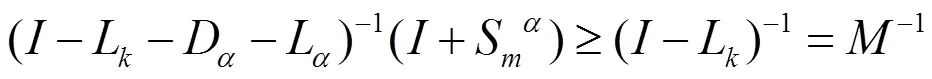
因为是一个非奇异-矩阵，

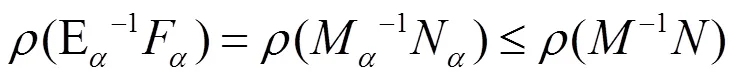
3 数值例子

考虑满足定理1条件的方程组(1)的系数矩阵，

令

[1] Kohno T, Kotakemori H, Niki H. Improving the Modified Gauss-Seidel Method for-matrices [J]. Linear algebra and its applications, 1997, 267: 113–123.

[2] Wu Mei jun, Wang Li, Song Yong zhong. Preconditioned AOR iterative method for linear systems [J]. Applied Numerical Mathematics, 2007, 57(5-7): 672-685.

[3] 刘庆兵,陈果良.预条件AOR和2PPJ迭代法收敛性的注记[J].华东师范大学学报:自然科学版,2009 (4):26-34.

[4] Li Wen, Sun Wei wei. Modified Gauss Seidel type methods and Jacobi type methods for Z-matrices [J]. Linear Algebra and its Applications, 2000, 317(1-3): 227-240.

[5] 周婷，郭文彬.-矩阵及其比较矩阵的预条件Gauss-Seidel法的收敛性[J]. 烟台大学学报:自然科学与工程版，2011，24(4)：260-263.

[6] Varga R S. Matrix Iterative Analysis [M].Berlin: Springer, 2000.

[7] Berman A, Plemmons R J. Nonnegative Matrices in the Mathematical Sciences [M]. SIAM, Philadelphia, PA, 1994.

[8] Frommer A, Szyld D. B.-splitting and two-stage iterative methods[J]. Numer. Math.,1992, 63(1): 345-356.

[9] Elsner L. Comparisons of weak regular splittings and multisplitting methods[J].Numer.Math,1989,56: 283-289.

[10] Li wen. Comparison results for solving precondtioned linear systems [J]. J. Comput. Appl. Math, 2005, 176(2): 319-329.

The convergence disscussion of the preconditioned Gauss-Seidel iterative method with a more general splitting

*ZHOU Ting, ZHANG Shi-guang

(College of Mathematics and Computer Science Hengshui University, Hengshui, Hebei 053000, China)

Using the Gauss-Seidel iterative method for the solution of the linear equations, the convergence of the Gauss-Seidel iterative method is discussed under a type of preconditioned matrix. With a more general splitting, we compare the convergence of the preconditioned Gauss-Seidel iterative method and the corresponding Gauss-Seidel iterative method. Furthermore, we get some comparison theorems. Finally, a numerical example is given to illustrate the validity of the conclusions.

precondition;-matrix;-matrix; Gauss-Seidel iterative method

1674-8085(2012)03-0013-03

O241.6

10.3969/j.issn.1674-8085.2012.03.003

2012-03-06；

2012-04-11

河北省高等学校科学研究计划项目(Z2010188);衡水学院2011年科学研究项目(2011026)

*周婷(1976-)，女，山东临朐人，硕士，主要从事数值计算方法及其应用研究(E-mail: zhouting7606@163.com);

张仕光(1975-)，男，山东平度人，讲师，硕士，主要从事广义逆理论及应用研究(E-mail: shiguang08@yahoo.com.cn).