稳态Y型和Ladder型双光子跃迁的对比

王德鑫，王伟浩，洪 滔

(哈尔滨师范大学)

0 引言

目前，在激光场驱动的多能级量子系统中，由于量子相干效应导致的电磁感应透明(EIT)技术已经取得了相当大的成功，是激光诱导量子相消干涉中控制原子的吸收和色散［1－2］中的一项有效技术.EIT的本质就是调整激光场以满足光与物质共振相互作用时在相关的原子态间建立量子相干和关联.且在很多方面有重要应用，例如光存储和提取［3－4］，无粒子数反转光放大(LWI)［5－6］，控制自发辐射相干，全光快速开关［7－8］，量子信息编码操作［9－10］，等等.因此EIT在不同领域有这么广泛的研究，不仅自由空间［11］，近几年 EIT技术已经发展到光腔中［12－13］，利用腔模的强耦合性与原子作用.到目前为止，大多数EIT系统都是伴随单光子吸收和辐射的原子跃迁.作为单光子EIT的拓展，双光子EIT［14］自1996年由Agarwal和Harshawardhan提出引起了广大学者的关注.很快，高锦岳研究组就分别在钠原子和铷原子气体中成功的实现了由一个耦合场控制两个弱探测场吸收［15］，实验上验证了Agarwal的理论.随后，严敏在倒Y模型系统中实现了基于量子相干抑制双光子吸收［16］.近年来，对双光子EIT的特性及其相关应用的研究也得到了飞速的发展［17－18］.研究范围也已经由封闭的原子系统发展到开放的分子系统［19－20］.

对印度学者Agarwal提出的模型及理论作了进一步的研究并设计一个新的模型与其进行对比.通过对数值结果及坠饰态理的分析，发现，这两种模型具有同样的光学响应.具体的结果和分析会在第二部分给出.

1 理论模型和方程

如图1所示，在三个激光场驱动的的四能级Y模型原子系统中，图1(a)，弱探测场Ep1和Ep2分别耦合|1〉↔|2〉和↔|4〉的跃迁，相应的激光场的频率为ωp1和ωp2.强耦合场Ec驱动|2〉↔|3〉的跃迁，其频率为ωc.在强耦合场作用下劈裂的坠饰态能级|2+〉和|2－〉(|2+〉=如图1(b)所示.单光子失谐Δp1=ω21－ωp1，Δp2= ω42－ωp2，Δc=ω32－ωc为激光场频率和原子能级跃迁频率的差，其中ω21，ω32，ω42是原子的跃迁频率.定义为拉比频率=是表征原子和激光场耦合强度的物理量.图1(c)是提出的一个四能级Ladder模型原子系统.其中，|2〉和|3〉是超精细结构的两个子能级.两个弱的激光场分别耦合了|1〉↔|2〉和|3〉↔|4〉的跃迁.为了方便，定义，相应的单光子失谐为Δp1=ω0－ω11－ωp1，Δp2=ω0－ω44－ ωp2.同样拉比频率定义为 Ωp1=在旋转波近似和偶极近似的条件下，Y模型和Ladder模型系统在相互作用图像下的哈密顿量分别为:

图1 系统模型(a)Y模型原子系统，(b)与Y模型等效的坠饰态结构，(c)Ladder模型原子系统

将其带入密度矩阵方程

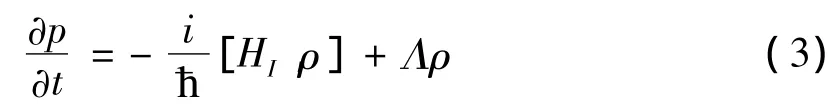
其中，Λρ包括自发辐射弛豫速率和相干弛豫速率.这样，就可以通过数值求解分别得到两个系统中四能级上的粒子数，进而分析双光子跃迁的情况.

在Y模型系统中，由于强场的耦合作用使得能级|2〉劈裂成两个坠饰能级.令方程(1)中的Ωp1=Ωp2=0，Δp1=Δp2=0，可以得到坠饰能级的本征值

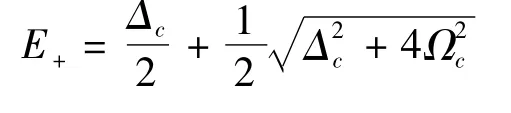
和本征态

两个模型中的双光子吸收率分别为:

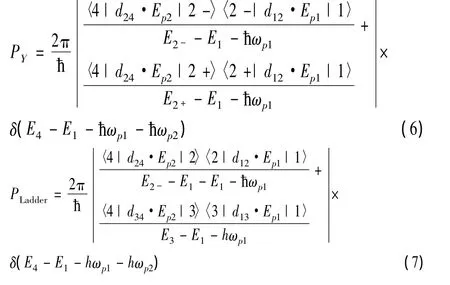
2 数值计算与分析

图2 双光子跃迁几率随探测场失谐Δp1的变化关系Δp2=0，Ωp1=Ωp2=0.01γ.黑色虚线，蓝实线和黑色实线分别对应Ladder模型中Δ1=10γ，30γ，50γ的情况，其中Γ21=Γ32=Γ42=Γ43=γ;红色虚线，粉色实线和橙色实线分别对应Y模型系统中Ωc=10γ，30γ，50γ的情况，其中Γ21=Γ32=Γ42=γ.

如图2所示，在两个弱探测场共振时双光子吸收被很好的抑制(即Δp1=Δp2=0时).同时，发现Y模型系统和Ladder模型系统具有相同的双光子吸收谱线线型，只是谱线的高度略有差别.这可以用坠饰态理论清晰的解释.由方程(4)可知Y模型系统坠饰态能级差ΔEY=E+－E－=2Ωc.通过前面的定义很容易得到Ladder模型系统中两个中间态的能级差ΔELadder=2Δ.在ΔEY=ΔELadder的情况下，两个系统具有相同的光学响应.这样，强场劈裂的坠饰态就被两个超精细结构能级所代替.也就是，在共振的条件下同时满足坠饰能级差与超精细能级差相等，两个中间能级为超精细结构的四能级Ladder模型可以代替在一个强场驱动下的四能级Y模型系统实现控制双光子的吸收和透明.同样，还可以通过双光子吸收率来解释.从方程(6)和(7)可知，当ω41=ωp1+ωp2时，PY=PLadder=0，这就通过控制失谐实现了双光子透明.此时，Y模型中的两个跃迁通道|1〉→|2+〉→|4〉和|1〉→|2－〉→|4〉分别等效于Ladder模型中的|1〉→|2〉→|4〉和|1〉→|3〉→|4〉两个跃迁通道.只是由于强耦合场的作用Y系统中四能级上的粒子数略多于Ladder系统.因此，强场不仅可用来劈裂坠饰态还能够影响粒子数的分布.

图3 光子跃迁几率随探测场失谐Δp1的变化关系黑色实线和黑色虚线分别对应Ladder模型中Δp2=Δ= 5γ，10γ的情况;红色实线，红色虚线分别对应Y模型系统中Δp2=Ωc=5γ，10γ的情况，其他参数与图2相同.

下面研究另外一种情况Δp2=Ωc(Y模型中)和Δp2=Δ(Ladder模型中)，如图3所示.这两个模型中双光子吸收峰不再对称，但是吸收谱线仍具有相同的线型.且在Δp1=Δp2=0处(即满足共振条件又保证共振处于两个坠饰能级之间)双光子吸收依然能被很好的抑制.同时，发现双光子吸收峰(Δp1=－Δp2)远大于单光子吸收峰(Δp1=Δp2处)，也就是在Δp1=－Δp2处双光子吸收被增强.而且，随着Δp2增加和Ωp1场远离共振，单光子吸收也逐渐被抑制.

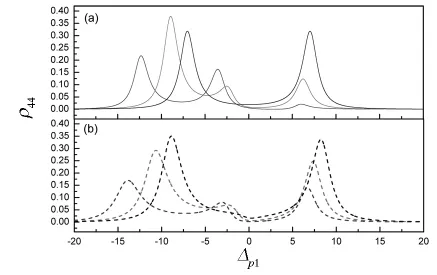
图4 双光子跃迁几率随探测场失谐Δp1的变化关系(a)黑色、红色和蓝色实线分别对应Y模型中Δc=0.0γ，5γ，10γ的情况;(b)黑色、红色和蓝色虚线分别对应Ladder模型系统中Δp2=0.0γ，5γ，10γ的情况.相应参数Ωp2= Δ=Ωc=5.0γ，其他参数与图2相同.

接下来，进一步研究双光子跃迁的吸收线型.将两个系统中第二个弱探测场换成强耦合场，并保证Ωp2=Δ=Ωc=5.0γ.如图4所示，同步改变Δc和Δp2的大小，发现这时两种模型仍具有相似的吸收谱线线型.但Δc=Δp2≠0吸收谱线出现了第三个峰.而且第三个峰的出现还是消失，在Y模型系统中取决于强场与原子的耦合程度.这是因为当Δc很大时，激光场与原子退耦合导致第三个峰消失.在Ladder模型系统中取决于第二个场的强度和两个超精细能级的差.

3 结 论

主要利用数值模拟的方法在相应参量值相同的情况下，对比了Y模型系统和Ladder模型系统的稳态双光子跃迁谱线.具体考虑三种情况.第一种情况:Y模型中强耦合场劈裂的两个坠饰能级等效于Ladder模型中两个超精细能级，同步改变Ωc和Δ的大小，谱线具有对称的吸收和透射;第二种情况:考虑第二个弱探测场与原子不共振时，导致了吸收谱线的不对称;第三种情况:将第二个弱探测场变为强场，同时保证两个系统在广场作用下的中间坠饰能级差始终相等，这样谱线在Δc=Δp2≠0时出现了第三个吸收峰.总之，通过对理论计算和分析发现，这两种模型具有同样的光学响应.

［1］ TewariSP，AgarwlGS.ControlofPhaseMatchingandNonlinearGenerationinDenseMediabyResonantFields［J］. PhysRevLett，1986，56:1811－1814.

［2］ HarrisSE，FieldJE，ImamoLUA.NonlinearOptical ProcessesUsingElectromagneticallyInducedTransparency［J］.Phys.Rev.Lett.，1990，64:1107－1110.

［3］ ChoiKS，DengH，LauratJ，etal.MappingPhotonicEntanglementintoandoutofaQuantumMemory［J］.Nature(London)，2008，452:67－71.

［4］ HamBS.ControlofPhotonStorageTimeUsingPhaseLoc－king［J］.Optics Express，2010，18:1704－1713.

［5］ Ling H Y.Theoretical Investigation of Phenomena in the Closed Raman－driven Four－level Symmetrical Model［J］. Phys Rev A，1994，49:2827－2838.

［6］ Zibrov A S，Lukin M D，Nlkonov D E，et al.Experimental Demonstration of Laser Oscillation without Population Inversion via Quantum Interference in Rb［J］.Phys.Rev.Lett.，1995，75:1499－1502.

［7］ Yan M.，Edwar Dward G.Rickey，Zhu Y F.Observation of Absorptive Photon Switching by Quantum Interference［J］. Phys.Rev.A.，2001，64:041801R－1－4.

［8］ Harris SE，Yamamoto Y.Photon Switching by Quantum Interference［J］.Phys Rev Lett，1998，81:3611－3614.

［9］ Yang G J，Qiu TH，Wang K，et al.Reversible Storage of a Weak Light Pulse in a Thermal Atomic Medium［J］.Physical Review A，2010，81:063817－1－8.

［10］Fleischhauer M，Lukin M D.Dark－state Polaritons in Electromagnetically Induced Transparency［J］.Physical Review Letters，2000，84:5094－5097.

［11］Xu JH，La Rocca GC，Bassani F，etal.Electromagnetically Induced One－photon and Two－photon Transparency in Rubidium Atoms［J］.Opt Commun，2003，216:157－164.

［12］Zhang JP，Hernandez G，Zhu Y F.Slow LightWith Cavity Electromagnetically Induced Transparency［J］.Opt Lett，2008，33:46－48.

［13］Hernandez G，Zhang JP，Zhu Y F.Vacuum Rabi Splitting and Intracavity Dark State in a Cavity－atom System［J］. Chin Phys B，2008，17:2885－2890.

［14］Agarwal G S，Harshawardhan W.Inhibition and Enhancement of Two Photon Absorption［J］.Phys Rev Lett，1996，77: 1039－1042.

［15］Gao JY，Yang SH，Wang D，et al.Electromagnetically Induced Inhibition of Two－photon Absorption in Sodium Vapor［J］.Phys Rev A，2000，61:023401－1－3.

［16］Yan M，Edward RG，Zhu Y F.Suppression of Two－photon Absorption by Quantum Interference［J］.Phys Rev A，2001，64:043807－1－4.

［17］ Chen JF，Lu W X，Wang SY，etal.Two－photon Freeinduction Decay with Electromagnetically Induced Transparency［J］.Opt.Lett.，2010，35:1923－1925.

［18］ Becerra F E，Willis R T，Rolston S L，et al.Two－photon Dichroic Atomic Vapor Laser Lock Using Electromagnetically Induced Transparency and Absorption［J］.J.Opt.Soc.Am. B，2009，26:1315－1320.

［19］ Qi J，Spano F C，Kirova T，et al.Measurement of Transition Dipole Moments in Lithium Dimers Using Electromagnetically Induced Transparency［J］.Phys Rev Lett，2002，88: 173003－1－4.

［20］Li L，Qi P，Lazoudis A，et al.Chem The Role of Doppler Broadening in Electromagnetically Induced Transparency and Autler－TownePhys Lett，2005，403，262.