具有复杂非线性环节的一类严反馈形式非线性系统的鲁棒自适应动态面控制

张秀宇，王建国，孙灵芳，付宏伟

(1.东北电力大学自动化工程学院，吉林吉林132012;2.华北电力科学研究院，北京100045)

磁滞是最重要的非平滑非线性环节之一，广泛存在于实际物理系统和装置中［1］。当一个装置受到磁滞非线性环节影响时，控制系统将产生诸如准确性降低、系统发生抖震甚至变得不稳定等严重问题［2］。工程应用中，磁滞现象的建模与控制是一个极具挑战性的问题。近年来，随着含有磁滞现象的智能材料的广泛使用，该问题亦受到研究人员的广泛重视［3］。

控制系统中磁滞环节的处理方法主要分为两大类:一类方法是在控制系统中引入磁滞现象的逆过程来抵消磁滞现象(详见参考文献［4］);另一类方法是在不建立磁滞你环节的情况下，利用鲁棒自适应控制策略来抵消或抑制系统中的磁滞现象。由于这种方法允许设计者采用各种鲁棒控制策略且便于稳定性分析，引起了控制领域学者的兴趣［5］。

在未建立磁滞逆环节的情况下，大部分控制策略都采用了自适应反推方法，这种方法在过去二十年中被广泛使用并且成为了解决非线性系统控制问题的重要方法［6］。但是，反推法的缺点也显而易见，存在所谓“微分爆炸”问题。

近年来，为了克服反推控制方法的缺点，受多滑模面控制方法的启发，Swaroop等学者最先提出了动态面控制方法［7］。目前，在一些文献中，也有用到动态面技术来处理一些非平滑非线性环节。

针对带有PI模型描述的磁滞现象的一类非线性系统，本文所提出的自适应动态面控制方案克服了采用反推方法所引起的“微分爆炸”问题。

1 系统描述

对于系统(1)有如下假设。

假设1系统中不确定项Δi(x，t)，i=1，…，n，为未知Lipschitz连续函数且满足

其中:ρi()为已知正光滑函数，bi为未知正常数。

假设2参考信号yr光滑、有界且对于t≥0，［yr，］T属于某一紧集。

假设3gi，i=1，…，n，的符号已知且存在一个常数gmin，使得gmin≤gi。不失一般性，我们假定gi＞0。

本文中所用到的PI磁滞模型如下:

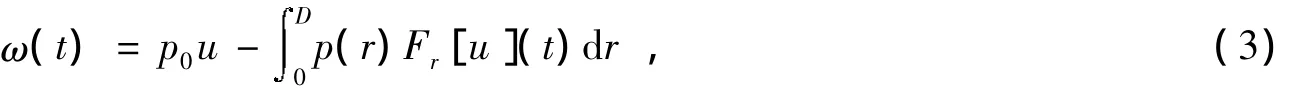
其中:p(r)为磁滞的密度函数，Fr［u］(t)为Play算子。现将(3)式代入(1)式可得，其中:β=gnp0(β＞0)，pg(r)=gnp(r)。

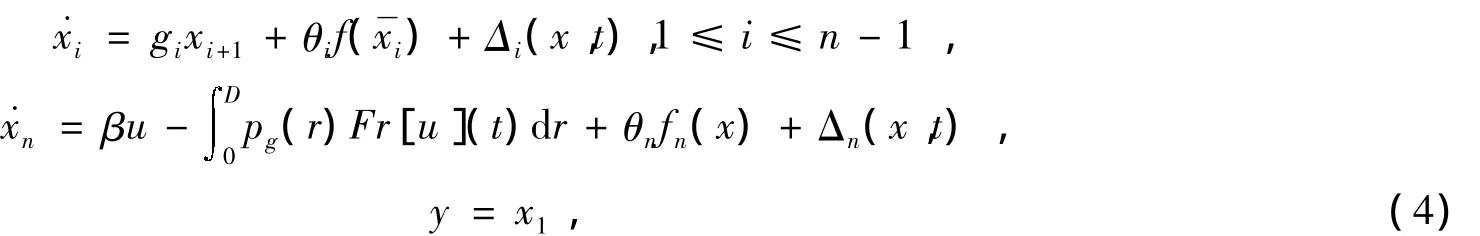
2 自适应动态面控制器设计

本文给出了自适应动态面技术来处理PI模型描述的磁滞现象的控制方案。整个设计过程共包含n步，实际控制律将在最后一步给出。

第1步定义第一个面误差(也是跟踪误差)为

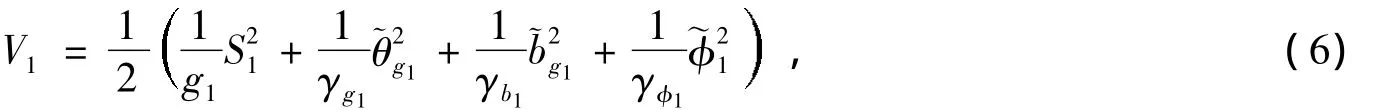
其中，yr为参考信号。考虑如下二次型方程其中，且分别为的估计值;γg1，γb1，γφ1为大于零的设计参数。因下述不等式成立:

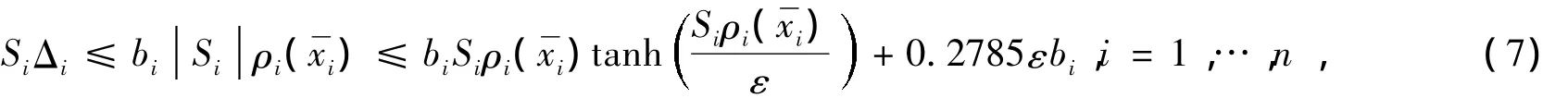
虚拟控制律x2d可设计为

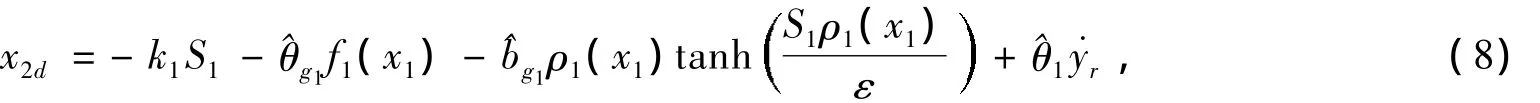
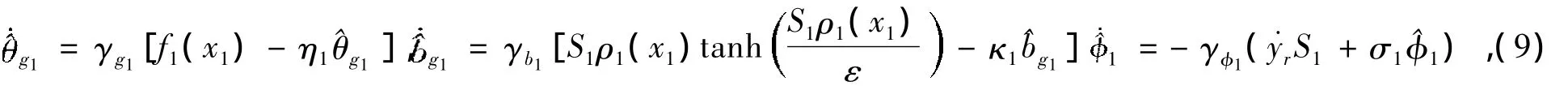
且η1，σ1，κ1为正设计参数。令x2d经过一阶低通滤波器获得的新变量x2，表示如下:

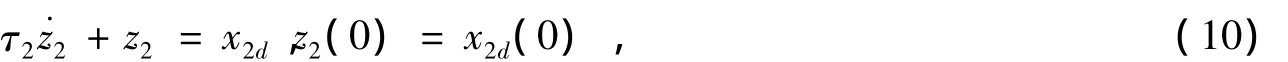
其中，τ2为滤波器时间常数。

第i步(2≤i≤n-1):定义第i个面误差为

其中:ci为正设计参数，c2，…，cn用来保证系统跟踪误差性能指标。考虑如下二次型方程

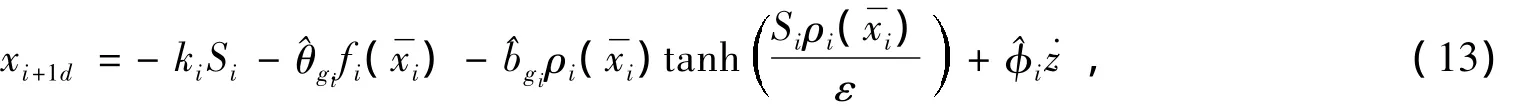
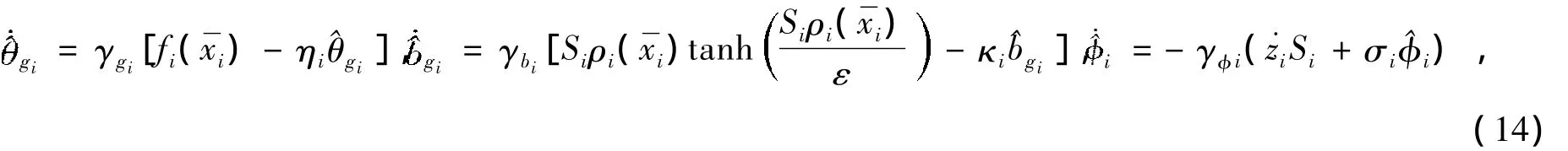
且ηi，σi，κi为大于零的设计参数。令xi+1d经过一阶低通滤波器获得的新变量zi+1如下所示:

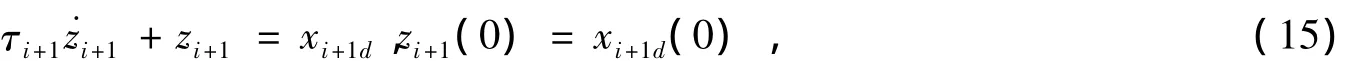
其中，τi+1为滤波器时间常数。

第n步定义第n个面误差为

我们考虑如下二次型方程

将设计u为

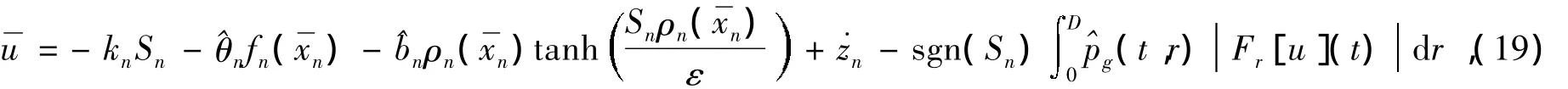
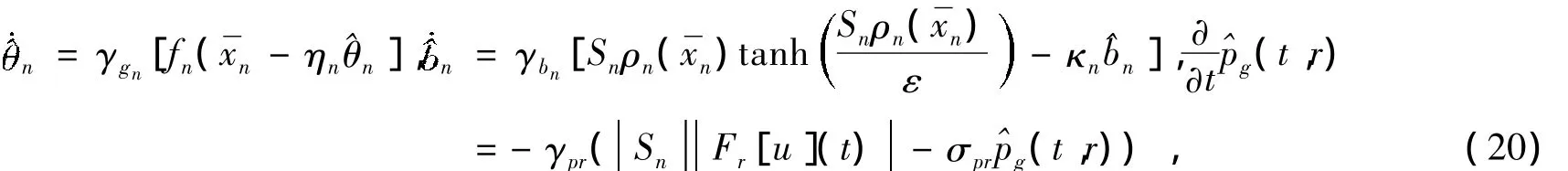
且ηn，σpr，κn为正设计参数。的调参律设计为

且ηζ为正设计参数。

3 稳定性分析

本对所提出的动态面控制方案采用Lyapunov稳定性分析方法进行稳定性分析。

定理1考虑由被控对象，一阶低通滤波器，实际控制律以及调参律所组成的闭环控制系统。若假设1-3成立。令Lyapunov函数定义为如下形式

其中:Vi已分别定义。对于任意给定的正常数p，若V(0)≤p成立，则存在ki，τi+1，γgi，γθi，γbi，γζ，γgn，γpr，γbn，ηi，σi，κi，ηn，σpr，κn，i=1，…，n-1，使得闭环系统所有信号半全局一致有界，且通过合理调整可调参数，系统的跟踪误差可收敛到任意小的邻域内。此外，通过设置系统的初始化条件，系统跟踪误差可满足性能指标。

证明:对Lyapunov函数V求导得

令

则当V=p时˙V≤0。这说明V≤p是一个不变集。若V(0)≤p，那么对于所有t≥0，V(t)≤p恒成立。可得

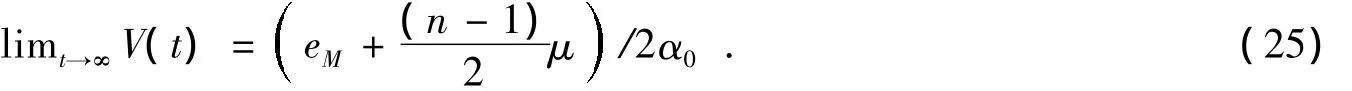
4 仿真算例

现考虑如下具有磁滞输入的二阶非线性系统:

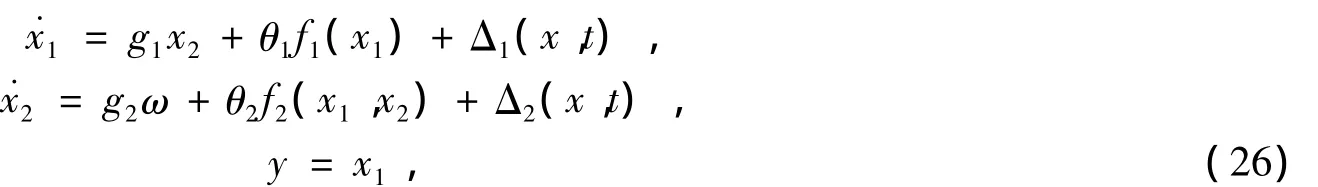
其中ω磁滞环节的输出，g1，g2为未知参数，Δ1和Δ2为扰动项。在仿真中，参数选择为g1=1.1，g2=1.1，θ1=0.12，θ2=0.01，f1(x1)=0.9，f2(x1，x2)=0，Δ1=0.2sin(x2)，Δ2=0.15(+)cos3t。因此b1=0.15，ρ1(x1)=1.5，b2=0.12，ρ2()=0.8+0.95。p(r)=0.5e-0.0014(r-1)2。控制目的是使系统输出y能够跟踪给定参考信号yr=sin(1.5t)。系统设计步骤如本文第三部分所示，这里不再详述。

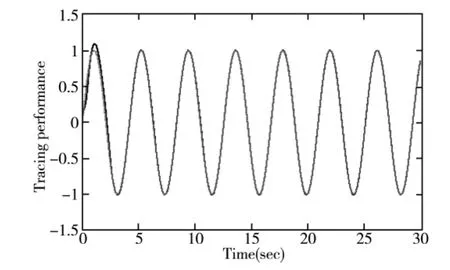
图1 磁滞补偿项存在时系统的输出y与参考信号yr(分别为实线和虚线)

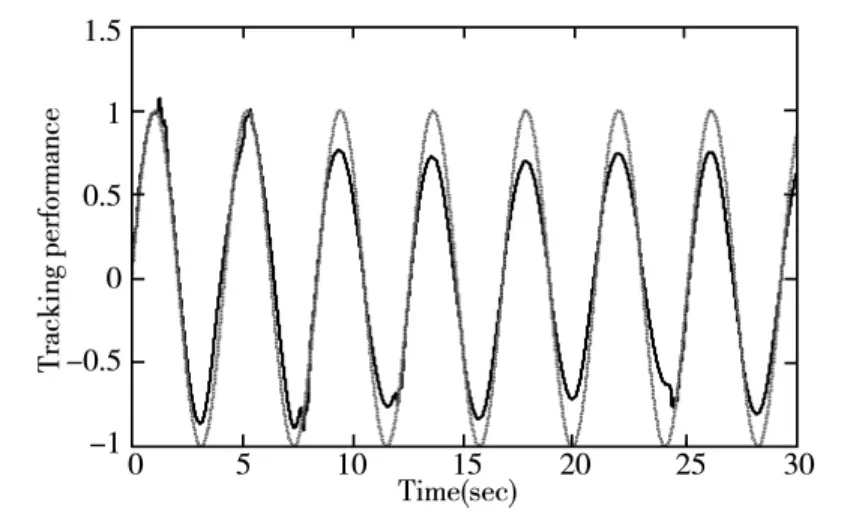
图2 没有磁滞补偿项时系统的输出y与参考信号yr(分别为实线和虚线)

［1］Mittal S.，Menq C.H..Hysteresis Compensation in Electromagnetic Actuators Through Perisach Model Inversion［J］.IEEE Transactions on Mechatronics，2000，5(4):394－409.

［2］Tao G.，Kokotovic P.V..Adaptive Control of Plants with Unknown Hystereses［J］.IEEE Transactions on Automatic Control，1995，40(2):200－212.

［3］Tan X.，Baras J.S..Adaptive Identification and Control of Hysteresis in Smart Materials［J］.IEEE Transactions on Automatic Control，2005，50(6):827－839.

［4］Moheimani S.，Goodwin G.C..Guest Editorial Introduction to The Special Issue on Dynamics and Control of Smart Structures［J］.IEEE Transactions on Control Systems Technology，2001，9(1):3－4.

［5］Zhang Xiuyu.，and Lin Y.A robust adaptive dynamic surface control for a class of nonlinear systems with unknown Prandtl-Ishlinskii hysteresis.International Journal of Robust and Nonlinear Control，2011，21(13):1541－1561，.

［6］Krsic M.，Kanellakopoulos I.，Kokotovic P.V..Nonlinear and Adaptive Control Design［M］.New York:A Wiley-Interscience Publication，1995.

［7］张秀宇，林岩.具有磁滞输入非线性系统的鲁棒自适应控制［J］.自动化学报，2010，36(9):1264－1271，

［8］Zhang T.P.and Ge S.S.Adaptive Dynamic Surface Control of Nonlinear Systems with Unknown Dead Zone in Pure Feedback Form［J］.Automatica，2008，44(7):1895－1903