回转干馏炉内颗粒停留时间的计算机模拟研究

王恭，苗宇，孙灵芳，刘宇峰

(1.东北电力大学自动化工程学院，吉林吉林132012;2.东北电力大学能源与动力工程学院，吉林吉林132012)

目前，随着国际油价的不断上升，人们越来越重视石油替代能源的开发，油页岩因其巨大的储量和广阔的开发前景已成为研究的热点。油页岩资源的开发模式多种多样，其中采用回转式干馏炉的固体热载体(热灰)干馏法具有资源利用效率高，便于维护的特点，在研究与实践中得到了重点关注。油页岩在干馏炉内的干馏过程主要受三方面因素影响:干馏炉的结构特点、油页岩的物料特性和干馏炉的操作参数。其中干馏炉的结构特点包括炉体尺寸、翻料机构型式及安装位置等;物料特性则主要有颗粒粒度、含油率、与固体热载体的混合比例等;操作参数则包括炉体的倾角、转速、填充率等。油页岩与固体热载体在干馏炉内的混合是一个非常复杂的过程，其混合效果决定了颗粒间的传热效果，最终影响到干馏过程的出油率［1］。研究表明，颗粒的混合效果与其在炉内的停留时间密切相关。然而在工程实践中，受工业现场客观条件的限制，无法对颗粒在回转炉内的混合过程进行准确的观察和分析。

随着离散元理论和计算机技术的发展，现阶段对于颗粒混合过程的仿真得到了越来越多的应用，它可以对实验难以实现的过程进行一定程度的分析和补充。乔斌等使用EDEM软件模拟了回转窑内石灰石的运动情况，研究了其停留时间的规律，并利用仿真结果修正了水泥行业回转窑内颗粒停留时间的经验公式［2］。刘安源等利用离散元法仿真分析了颗粒在振动给料机中的运动规律并归纳总结了实验数据，得出了不同振动参数对颗粒运动影响的规律［3］。欧阳鸿武等人则在分析粉体混合过程的基本特征和混合机制的基础上，介绍了数值模拟的理论基础并对近年来数值模拟研究及实验研究进展进行了总结［4］。离散元分析方法与计算流体力学相结合可以发挥各自在建模及数值分析的优势，近年来也得到了重点研究。潘振海等将离散元素法(DEM)与计算流体力学(CFD)方法结合起来，利用DEM的粒子轨迹、碰撞等力学的计算方面的优势以及CFD在流体计算方面的优势，模拟了矩形管内液固两相的流动过程，分析了颗粒在流体的带动下在矩形管中的运动规律［5］。卢洲针对物料在气力输送过程中特别是弯管部分易破碎的问题，采用CFD和DEM耦合模拟弯管内的柱状颗粒气力输送过程，将EDEM与FLUENT耦合，模拟了颗粒在弯管处的输送过程，对球形颗粒与柱状颗粒在弯管处的运动规律进行了比较，分析了不同弯径比下管壁在传送过程中的力学特性［6］。

本文以回转式油页岩干馏实验系统为研究平台，通过合理简化与假设，实现了炉内结构的建模。同时，以离散元素法为理论基础，在设定一定的颗粒特性、填充率及炉体转速的条件下，对三种炉体倾角下的颗粒停留时间进行了仿真研究。仿真分析有助于设备结构型式的改进以及操作工况的优化。

1 离散元素法基本原理

离散元素法的基本思想是将所研究对象划分为一个个相互独立的单元，根据单元之间的相互作用和牛顿第二运动定律，采用动态或静态松弛法等进行循环迭代计算，以确定每个时间步长中对象单元的受力及位移情况，并更新所有单元的位置。通过跟踪计算每个单元的微观运动情况，即可获得整个研究系统的宏观运动规律。离散元的基本假设是:选取的时间步长足够小，使得在一个单独的时间步长内，除了与选定的单元直接接触的单元之外，来自其他任何单元的扰动都不能传播过来;并且规定在任意的时间步长内，速度和加速度恒定［7］。

在离散元素法中，固体颗粒在空间的运动分解为平动和转动两种模型来进行分析处理，单个颗粒的运动行为是这两种运动的叠加。

根据牛顿第二运动定律，颗粒的平动运动方程为

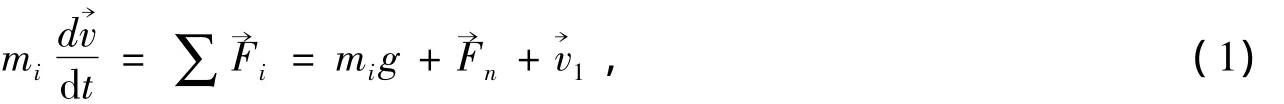
式中:mi为颗粒i的质量(Kg)是其速度(m/s)，∑为其所受的作用力的合力(N)，→Fn表示颗粒i所受的法向接触力(N)，→Fi表示其切向接触力(N)。

颗粒的转动方程为

式中Ii是颗粒i的转动惯量(Kg/m2)是颗粒i的角速度(rad/s)，∑是由颗粒间碰撞而对颗粒i产生的扭矩总和(Kg/m)。/dt即颗粒i的角加速度(rad/s2)。当颗粒j与颗粒i发生碰撞时，作用在颗粒上的扭矩用公式(3)计算。

2 油页岩固体热载体干馏实验系统

油页岩固体热载体干馏实验系统如图1所示。由混合进料系统、回转干馏炉、油气回收系统、角度调节机构等几个子系统组成。混合进料通过变频器调节电机带动螺旋式给料杆将颗粒送入干馏炉。回转干馏炉为圆筒式结构，其中内径D为125 mm、长度L为600 mm;炉体内部沿轴向均匀布置6块抄板:直板段长度为28 mm，弯板段长度为8 mm。干馏炉由电机带动回转，当固体热载体与油页岩在炉内充分混合后，混合物从出口进入集灰器。整个反应过程产生高温油气及含有半焦的灰渣，高温油气经旋风分离器二次分离、冷却收集到集液箱，而半焦及灰分通过集灰器出口送出。

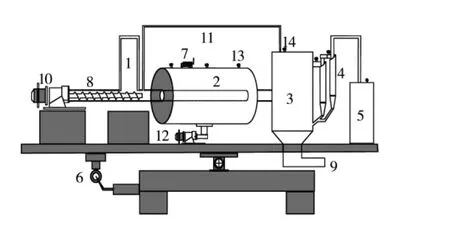
图1 回转式油页岩干馏实验系统

3 仿真模型的建立

根据离散单元法，并结合散体动力学，本文主要做如下假设:①当回转炉内颗粒填充率、转速、倾角等工况不变时，颗粒在炉内各段的运行状况相同;②颗粒参数、炉体及翻料构件材料参数为所设定值，在分析的全过程中不发生变化;③物料在炉内的运动包括升举和抛落两种过程，一个单元内物料的停留时间视为两者之和;④自由面上颗粒的滚落过程仅受重力支配，飘落过程中的轴向位移唯一决定颗粒的轴向移动距离，料床底部物料仅随炉体转动，且不产生轴向位移;⑤忽略横向和轴向扩散及出口效应。

3.1 参数设置

结合上述假设及实际系统工况和结构，选择颗粒半径为2 mm，材料及接触参数如表1、2所示。

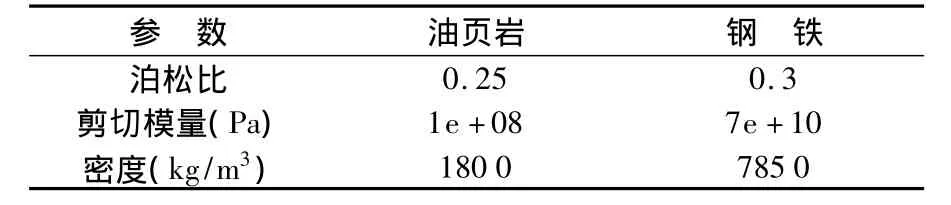
表1 材料参数

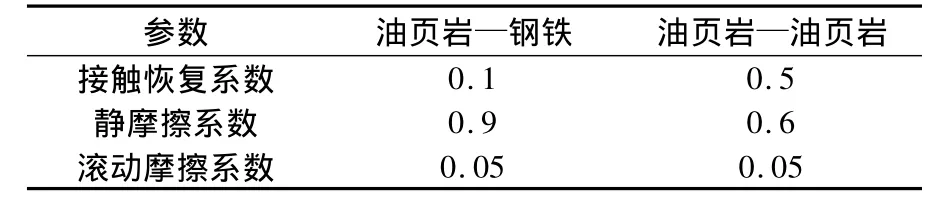
表2 材料接触的相关系数

3.2 系统建模

系统建模主要包括炉体结构建模以及颗粒生成，使用Gambit软件建立几何模型，如图2、3所示。物料由螺旋叶片送入炉内，为加快计算速度，炉体段长度设置为30 mm。通过对数据的观察估算，调整螺旋叶片的送料量，使每秒钟进出30 mm滚筒横截面颗粒数目基本吻合，从而保持炉内填充率。研究表明，颗粒在炉内发生轴向位移主要受抛落运动影响，为模拟实际工况，在炉体出口处设计一内径为28 mm，外径为32 mm的圆环挡板，其法线方向为颗粒运动方向，即仿真坐标系中的Z+方向。

图3 炉内颗粒生成

图2 炉体结构建模

3.3 工况设置

在完成颗粒生成过程后，由于最初颗粒为随机生成，其在滚筒内的分布不太均匀，为与实际情况更为符合，设置炉体在不添加轴向加速度的情况下旋转一定时间以使颗粒均匀混合。混合完成后，炉内约有1 800粒颗粒，填充率约占炉体的30%。同时为保证填充率的稳定，在炉体前方螺旋叶片处生成颗粒以进行补充，如图4所示。

图413 s时颗粒在炉内分布基本均匀

图5 示踪粒子的选取

设置炉体以10 r/min的速度逆时针旋转，炉体倾角分别为2.16°，3.24°，4.33°。由于针对不同倾角进行仿真，因此重力加速度会在Y－以及Z+产生不同的加速度分量，取当地重力加速度为Y－方向9.8 m/s2，则对应三个倾角的各方向重力加速度如表3所示。

表3 不同倾角下重力加速度的设定

4 实验结果及分析

4 .1实验结果

为观察颗粒在炉内的停留时间，在每个工况中选取螺旋叶片中靠近炉体侧的20粒颗粒跟踪观察其运动情况，图5为倾角为3.24°时选取的示踪粒子图。以所选所有颗粒全部离开炉膛为仿真结束时间。

颗粒在炉内升举及抛落时，其运行轨迹类似抛物线，连续的运转实现从炉膛内侧到外侧的Z+方向位移。对于每个倾角下所选择的20个颗粒，为描述方便，按其在各自仿真工况中生成编号从小到大的顺序，编为1－20号。三种倾角下的停留时间统计结果见表4，计算后的平均停留时间分别为9.51 s、8.44 s和6.67 s。

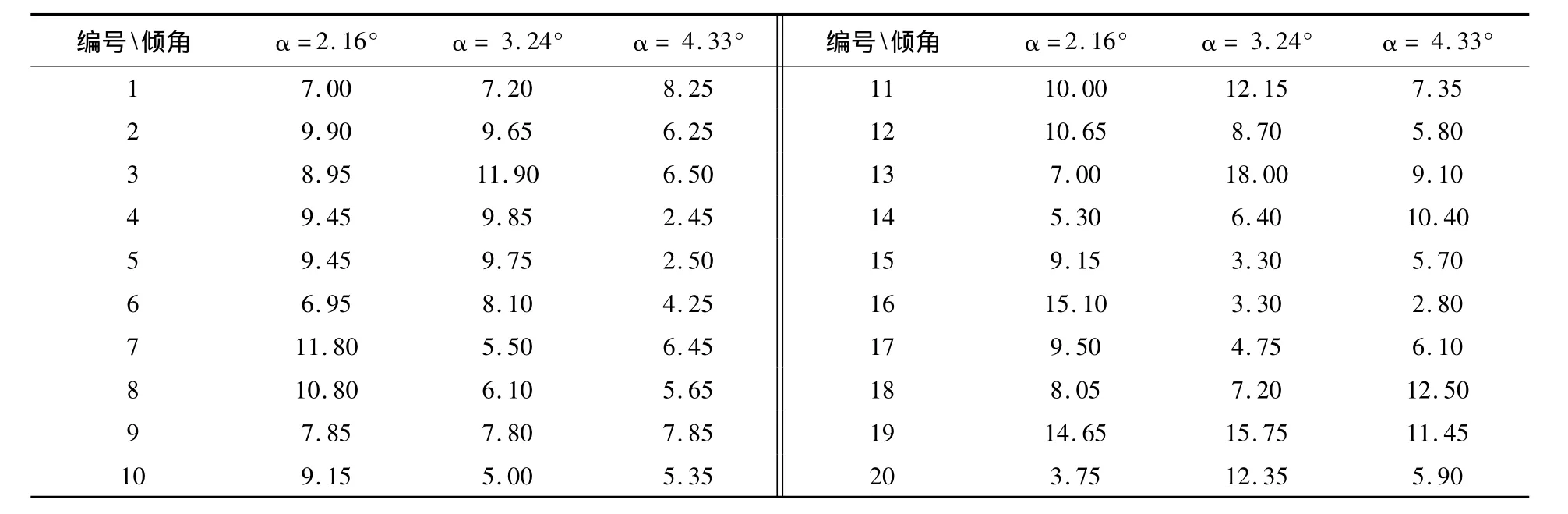
表4 三种倾角下颗粒的停留时间(s)

倾角不同时停留时间分布情况如图6所示。分布结果符合正态分布规律，同时随着倾角的加大，物料的平均停留时间越来越短。根据文中假设，认为颗粒在炉内各段运动规律一致，通过对30 mm的仿真结果预测在600 mm完整长度内颗粒的平均停留时间，则对应2.16°、3.24°、4.33°三种倾角的平均停留时间分别为3.17 min、2.81 min、2.22 min，与文献［10］的实验结果基本一致。

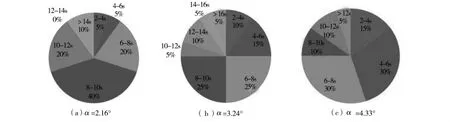
图6 倾角不同时停留时间分布图

5 结论

固体热载体干馏法广泛应用于页岩油的提炼，仿真的方法可以为干馏炉内颗粒混合的分析提供一种新的研究手段。通过对系统的分析及对模型的合理简化，以离散元素法为理论基础，在填充率为30%、炉体转速为10 r/min条件下，分析了炉体3种倾角时的颗粒停留时间。结果表明，炉内颗粒的平均停留时间随着炉体倾角的增大而减少;虽然单个颗粒的停留时间具有一定的随机性，但从总体观察其平均停留时间在一定时间区间内则相对集中。仿真结果对于观察和分析干馏炉内颗粒的运动规律，具有一定的参考价值。

［1］钱家麟，尹亮.油页岩—石油的补充能源［M］.北京:中国石化出版社，2008，81－88.

［2］乔斌，朱玲利，雷晓娟.基于EDEM软件的石灰石在回转窑内停留时间的模拟研究［J］.矿山机械，2012，38(19):83－85.

［3］刘安源，刘石，潘忠刚.振动给料机中固体颗粒物料运动规律的数值研究［J］.中国科学院研究生院学报，2002，19(1):35－42.

［4］欧阳鸿武，刘泳，陈海林，等.粉体混合过程的实验和数值模拟研究［J］.材料导报，2003，17(8):5－7.

［5］潘振海，王昊，王习，等.油砂干馏系统的DEM-CFD耦合模拟［J］.天然气工业，2008，28(12):124－126.

［6］卢洲，刘雪东，潘兵.基于CFD-DEM方法的柱状颗粒在弯管中输送过程的数值模拟［J］.中国粉体技术，2011，17(5):65－69.

［7］胡国明.颗粒系统的离散元素法分析仿真［J］.武汉:武汉理工大学出版社，2010:7－8.

［8］Nakashima H.Discrete Element Method(DEM)and its possible application.SICE 2004 Annual Conference.Japan:Hokkaido Institute of Technology.2004，2:1004－1007.

［9］Zhao L L，Liu C H，Zhang Y，et al.Computer Simulation of Particle Segregation Process Using 3D Discrete Element Method.2009 International Conference on Computational Intelligence and Software Engineering.Wuhan:CISE，2009:1－3.

［10］李少华，张立栋，余侃胜，等.回转干馏炉油页岩颗粒停留时间分布［J］.华北电力大学学报，2011，38(1):98－102.