保费随机收取的二维风险模型的破产概率
2012-03-12黄玉娟于文广
黄玉娟,于文广
(1.山东交通学院理学院,济南250023;2.山东财经大学保险学院,济南250014)
0 引言
在经典的保险风险理论中,复合泊松风险模型U(t)=u+ct-S(t)是主要的研究对象,并且取得了许多经典的结果[1][2]。随后许多学者对该风险模型进行了各种各样的推广,其中之一就是将一维模型推广到多维风险模型。近年来随着保险数学的研究,多维风险模型也越来越受到关注,但是多维风险模型在数学处理上较为复杂,即便是二维风险模型在技术处理上也较为困难。文献[3]构造了一个二维风险模型,定义了三类破产概率,给出了关于破产概率的一个简单的界,得到了理赔额服从phase-type分布时的破产概率的确切表达式。文献[4]对多维风险模型破产概率进行了研究,并将同一索赔事件产生的几种索赔之间的相关关系考虑了进来,应用多维Phase-type分布得到了几种不同形式破产概率的边界。文献[5]、[6]研究了索赔相关的双Poisson二维风险模型的破产概率。文献[7]、[8]分别讨论了索赔为轻、重尾分布的二维风险模型的破产概率。文献[9]把索赔到达过程推广到Poisson过程且每份保单的理赔额也推广为随机变量,得到了相关风险模型的破产概率及其上界。基于上述文献,本文将稀疏过程引入到二维风险模型中,将收取新保单和由续保收到的保单区别开来,即索赔以Poisson流到达到的同时会产生一个强度为λρ(0<ρ<1)续保的Poisson过程,同时新保单也以Poisson流到达。
1 模型的定义与实际背景
定义1设u1≥0,u2≥0,c>0,α>0,在给定概率空间(Ω,F,P)上,定义二维风险模型为:

其中,ui≥0是第i个保险公司盈余过程{Ui(t);t≥0}的初始资本,i=1,2;c为单位时间内收到的保费;{Wi(t);t≥0}为一标准维纳过程,表示第i个保险公司的不确定的收益和支付,i=1,2;α为大于零的常数,表示扩散扰动强度。{Mi(t);t≥0}为直到t时收到的新保单数,服从参数为 βi的泊松过程,i=1,2;{N1(t);t≥0}表示[0,t]内的总理赔次数,其速率为 λ1的泊松过程;{Yik≥0;k=1,2,...}表示第i类险种第k次的理赔额,且独立同分布,E[Yik]=μiy,Var[Yik]=σ2iy,i=1,2;{Xik≥0;k=1,2,...}表示第i类险种第k次续保费,且独立同分布,E[Xik]=μix,Var[Xik]=σ2ix,i=1,2,并设μiy>μix;{N2(t);t≥0}表示[0,t]内续保保单以速率λ1ρ (0<ρ<1)的泊松过程到达,即{N2(t);t≥0}是{N1(t);t≥0}的ρ-稀疏过程。ρ的实际意义为考虑这样一类险种,它由两个相关的风险类构成。每一类都有两种理赔方式,主理赔与次理赔,即某一类风险理赔的发生会以某概率ρ的可能性产生次理赔。例如,在一次交通事故中,车辆发生意外造成损坏,同时人身也可能受到伤害,那么可以把车险看作主理赔,人身保险看作次理赔。
令


则(1)式可以改写为
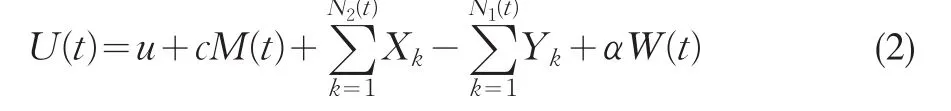
假设1{N1(t);t≥0}与{Yk≥0;k=1,2,...}、{Xk≥0; k=1,2,...}、{M(t);t≥0}和{W(t);t≥0}是相互独立的。{Y1k≥0;k=1,2,...}和 {Y2k≥0;k=1,2,...}相互独立;{X1k≥0;k=1,2,...}和{X2k≥0;k=1,2,...}相互独立。
以上我们定义了稀疏过程下的二维风险模型,但二维风险模型的破产定义与一维风险模型的情况是有区别的。首先,给出一维风险模型两个盈余过程{U1(t);t≥0}和{U2(t);t≥0}的破产时刻和破产概率的定义。定义Tj为第 j个盈余过程的破产时间 j=1,2,即Tj=inf{t|Uj(t)<0}及第 j个盈余过程的破产概率ψj(uj)= Pr(Tj<∞|Uj(0)=uj)。
下面给出二维风险模型的三类破产时刻的定义:
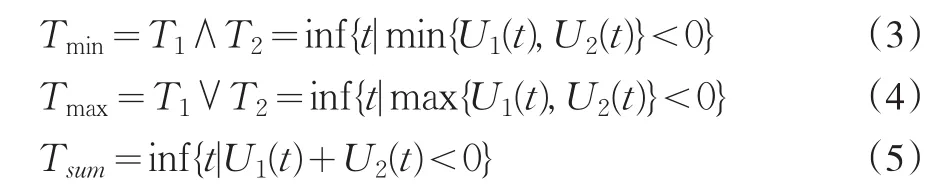
相应的破产概率分别定义为:

注以上定义的实际背景为,{Tmin<∞}表示U1(t)和U2(t)中至少有一保险公司的盈余过程为负值,即在将来的某个有限时刻t,至少会有一个保险公司发生破产;{Tmax<∞}表示在将来某个有限时刻t,其盈余U1(t)和U2(t)都会为负值,即两个保险公司在将来有限时刻t均会发生破产;{Tsum<∞}表示U1(t)与U2(t)的和会为负值,即两个风险过程的和将来在有限时刻t会为负值,即破产发生。因此,与一维保险风险模型相比,其破产概率满足如下关系:

且根据定义有
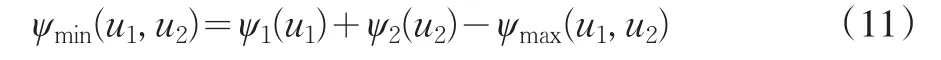
下面对Tmin进行讨论。首先考虑其对应的生存概率:
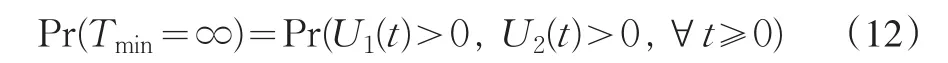
引理1给定两个实数{x1,x2},则如果它们都为严格正值当且仅当对所有严格正实数{a1,a2},都有 a1x1+a2x2>0。事实上,引理条件只需要a1>0, a2>0及a1+a2=1。

所以,由引理1和(12)式可知:下面定义一个参数为a={a1,a2}的一维风险模型:

令

定义盈余过程{Ua(t);t≥0}的破产时刻为Ta=inf {t≥0|Ua(t)<0},则其想应的破产概率定义为:

运用现代概率论相关知识,可得Tmin和Ta如下关系:

类似地,(7)式中定义的破产概率ψmax(u1,u2)满足:

特别的,当 a1=1/2,a2=1/2,可以得到 Pr(Tsum<∞)=Pr(T{1/2,1/2}<∞)。因此,破产概率Pr(Tsum<∞)可以简化为一维风险模型的破产概率。
2 主要结果
定理1盈利过程{Sa(t),t≥0}具有下列性质:
(1)Sa(0)=0;(2){Sa(t),t≥0}平稳独立增量;(3)存在正数r>0,使得E[exp(-rSa(t))]<∞。
定理2对于盈利过程{Sa(t),t≥0},存在函数g(r)使得E[exp(-rSa(t))]=exp(tg(r))。
证明:E[exp(-rSa(t))]

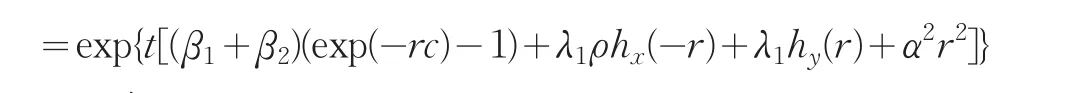
令
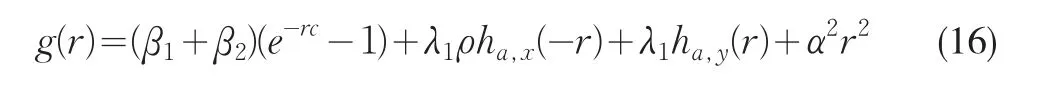
即可。
定理3方程g(r)=0在r>0内有唯一正解Ra,Ra称为模型(14)的调节系数,而g(r)=0称为调节系数方程。
证明:只需证明g(r)具有以下4条性质即可。

显然g(0)=0,则①式成立。
由于

则g′(0)<0,而

故g(r)在r的非负半轴上是下凸函数,所以g(r)=0至多有两个解,而r=0为平凡解,故r>0内有唯一正解r=Ra。
定理4设Ra为调节系数,A为X和Y的上界,则调节系数Ra满足如下不等式

证明方法类似文献[10]。
对于盈利过程{Sa(t),t≥0},定义=σ{Sa(v);v≤t}为{Sa(t),t≥0}的自然σ-域流。
定理5Ta是的停时。
定理6{Mˉa(t),t≥0}是鞅,其中:

定理7对于任意实数r,其最终破产概率满足:

证明:对任意固定常数t0,t0∧Ta为有界停时,从而由鞅的停时定理可得:
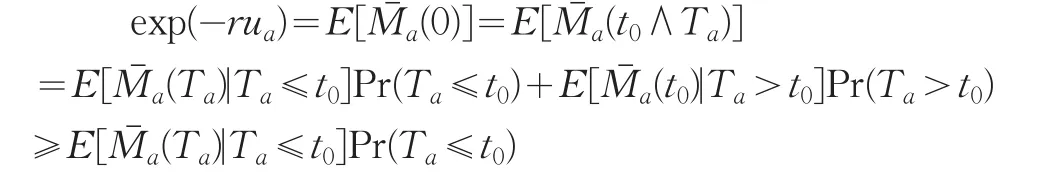
所以

对上式两边取期望并令t0→∞,则可得(18)式。
定理8盈余过程{Ua(t);t≥0}的最终破产概率满足:
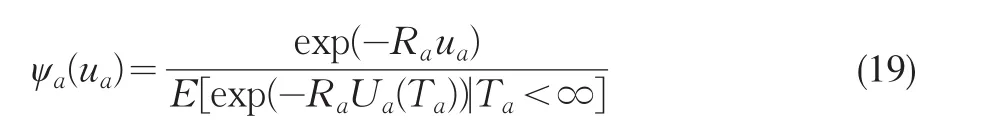
证明对任意的固定常数t0,t0∧Ta为有界停时,从而由有界停时定理可得:

在上式中,取r=Ra得:

若令I(C)表示集合C的示性函数,则有:

由于0≤exp(-RaUa(t0))I(Ua(t0)≥0)≤1,根据大数定理可证明当t0→∞时,Ua(t0)→∞(几乎处处),由控制收敛定理有(几乎处处),从而当t0→∞时,式(20)即可化为(19)式。
推论1{Ua(t);t≥0}的最终破产概率所满足的Lundberg不等式为:

其中,Ra为调节系数。

[1]Grande J.Aspect of Risk Theory[M].New York:Spring-Verlag,1991.
[2]Gerber H U.数学风险论导引[M].成世学,严颖译.北京:世界图书出版发行公司,1997.
[3]Chan Wai-Sum,Yang Hailiang,Zhang Lianzeng.Some Results on Ruin Probabilities in A Two-dimensional Risk Model[J].Insurance: Mathematics and Economics,2003,(32).
[4]Cai J,Li H J.Multivariate Risk Model of Phase Type[J].Insurance: Mathematics and Economics,2005,(36).
[5]马学思,刘次华.双Poisson二维风险模型的破产概率[J].统计与决策,2006,(8).
[6]陶金瑞,张永珍,刘俊先.二维相依泊松风险模型的破产概率[J].南开大学学报(自然科学版),2009,42(4).
[7]李祥发,宋会杰,郭鹏江.扰动的二维风险模型的破产概率[J].西北大学学报(自然科学版),2009,38(6).
[8]颜荣芳,潘欢.重尾环境下二维风险模型在有限时间内的破产概率[J].兰州大学学报(自然科学版),2008,44(2).
[9]杨恒,黎锁平.改进后的二维相关风险模型[J].甘肃科学学报, 2010,22(1).
[10]于文广,黄玉娟.随机利率因素下的多险种破产模型[J].临沂师范学院学报,2006,28(6).
