基于图形的黑体辐射三大基本定律关系阐述

徐代升 王元樟

（厦门理工学院数理系；厦门理工学院光电工程技术研究中心，福建 厦门 361024）

某一温度目标的光谱辐射出射度分布曲线、给定波段辐射出射度、总辐射出射度、给定波段辐射出射度与总辐射出射度比、指定波长辐射出射度、峰值辐射波长及峰值辐射出射度等这些光电探测系统设计过程中，对探测对象——目标热辐射特性的分析计算所必须知晓的参数，是光电探测系统设计中首先要涉及的技术问题.黑体辐射的三大基本定律，即普朗克辐射公式、维恩位移定律和斯忒藩－玻尔兹曼定律，是分析光源辐射特性的理论基础.因此在光电技术、光辐射测量原理与技术、光学传感与测量、照明工程等许多课程中都会涉及三大基本定律的教学.但是，近年出版的许多教材［1～3］，在论述上述三大定律时，篇幅都比较少，大多直接给出结论，没有充分阐明每一个定律的物理含义及它们之间的相互关系.如果教师在教学时照本宣科，那么学生掌握黑体辐射三大基本定律的效果肯定不佳，更谈不上在处理光电工程问题时，灵活应用这三个基本定律了.笔者应用相关课题研究成果，在有关课程中讲述三大定律时，从普朗克辐射公式作图出发，结合图形阐述三大定律的物理含义、彼此间的相互关系以及在工程实践中灵活应用的问题.

1 普朗克辐射公式及其作图

现在的教材在讲述普朗克辐射公式时，基于课时和学生基础不够的缘由，一般都不对其作推导（如采用经典量子统计方法），而是直接给出公式的表达式.普朗克辐射公式所表达的是黑体的光谱辐射出射度，其表达式为

其中，Mbλ为黑体的光谱辐射出射度（W·m－2·μm－1）；λ 为波长（μm）；T 为温度（开尔文温度、K）；k为玻尔兹曼常数（k＝1.380662×10－23J·K－2）；c1为第一辐射常数（c1＝3.741832×10－16W·m2）；c2为第二辐射常数（c2＝1.438786×10－2m·K）.

教学时若只是对着式（1）来解释普朗克辐射公式，一般来说学生会听得“云里雾里”.为了真正让学生了解普朗克辐射公式，下面通过编程作图来阐明.前面已说明普朗克辐射公式所表达的是黑体的光谱辐射出射度，为此以波长λ为横坐标，Mbλ为纵坐标，辐射温度T 为变量，用Matlab［4］编程给出的Mbλ、λ、T 三者的关系图.

程序代码如下［5］：

图1是上述Matlab代码编译后给出的Mbλ、λ、T 三者的关系图，图中所有的标注、连线都是由程序给出的.

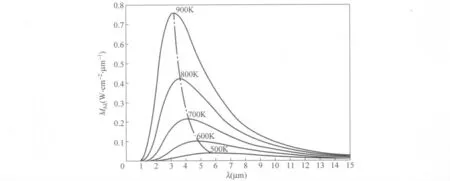
图1 各种温度下的黑体光谱辐射出射度曲线

从图1中的曲线可以明显地看出黑体辐射的一些特性，并由此建立普朗克辐射公式与维恩位移定律和斯忒藩－玻尔兹曼定律的关系.

2 维恩位移定律

由图1可知，黑体光谱辐射出射度Mbλ随波长λ 连续变化，某一辐射温度下对应的一条曲线有一个极大值，即该辐射温度下黑体的峰值辐射出射度，峰值所对应的波长叫峰值波长λm.对于连续曲线，由数学知识可知，对其求导并令其为零，可求出曲线的极值点.因此用普朗克公式对波长求导，并令其为零，可推导出峰值波长λm与黑体绝对温度T 的关系表达式

此式即维恩位移定律.图1中的点划线就是峰值波长的连线.从峰值波长的连线可以看出，随着温度的升高，峰值波长减小，即随温度升高，黑体辐射中包含的短波部分所占的比例增加.

在光电探测系统中，可利用维恩位移定律计算出辐射源（目标）某一温度下的峰值波长，从而确定选用的红外探测器响应的峰值波长，实现所谓“光谱匹配”.从图1中还可以看出，峰值波长左右两边一定波长范围内，是给定温度下黑体或近似黑体物体辐射出射度最多的波段，因此，维恩位移定律还有助于选用探测器实现所谓“波段匹配”.通常把地面目标看成辐射温度为300K 的灰体，则其峰值辐射波长为9.6593μm，所以通常选用在波长范围为8～12μm（也考虑了大气窗口因素）响应度较高的探测器，如MCT，作为其探测装置的优选传感器.关于这点，下面论述波段辐射出射度如何计算时还将进一步说明.

3 斯忒藩－玻尔兹曼定律

从图1还可以看出，黑体的辐射特性只与黑体的绝对温度有关.图1中各条曲线彼此不相交，温度越高，在所有波长上的光谱辐射出射度也越大.反之亦然.由积分概念可知，图1 中每条曲线下的面积代表黑体在给定温度下总的辐射出射度.因此把普朗克公式对波长从0到∞积分，就可得出黑体总的辐射出射度与温度的关系

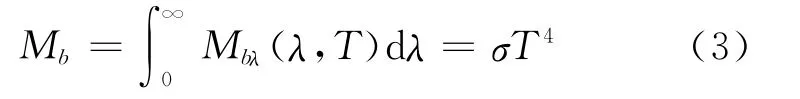
其中，σ＝（5.67032±0.00071）×10－12（W·cm－2·K－4），是斯忒藩－玻尔兹曼常量.式（3）即斯忒藩－玻尔兹曼定律.该定律表明，黑体总的辐射出射度与温度的四次方成正比，因此，当温度T 有很小的变化时，就会引起辐射出射度的很大变化.这一点从图1每条曲线下的面积也可以看出，随着温度的升高，曲线下包围的面积显著增大，即意味着黑体总的辐射出射度随温度升高而迅速增大.

4 黑体目标波段辐射出射度计算

式（3）斯忒藩－玻尔兹曼定律给出的是黑体目标总的辐射出射度.实际工程应用中，更关心的是得到某一温度下某一波段λ1～λ2范围内的辐射出射度以及该波段内的辐射功率占总辐射功率的百分比.从的本意来讲，它应为

但是上式的实际积分十分复杂，写不出显性表达式.为了计算这一参数，人们探索了许多巧妙的方法，甚至出版了厚达几百页的黑体辐射特性数据表这样的书［6］，供设计者在工程实践中查表使用.

数值积分方法可通过构造函数调用所选程序设计语言中的相关函数来进行，这里在保证计算精度的要求下，通过设定积分步长选用矩形积分法进行，具体实现方法可参考笔者研究成果，参见文献［7］.图3是由文献［7］所述热辐射可视化计算软件给出的4980K 黑体辐射目标、辐射波段为0.2～4.2μm 的波段辐射出射度的结果.对于4980K 黑体辐射目标，辐射波段为0.2～4.2μm时，其，占总辐射出射度的比例为98.69%.

在进行光电探测器选择时，“光谱匹配”一般不可能完全满足，这时就应尽可能使选用的探测器响应的波段范围位于目标辐射体峰值辐射波长的两侧，响应波段范围内的辐射出射度占总辐射出射度的比例尽可能多，即“波段匹配”.目前在聚光光伏太阳能系统中，正大力开发三界面InGaP/GaAs/Ge太阳能电池，来扩大对太阳光波长的吸收范围（可吸收300～1500nm 波长）以提高太阳能电池的转化效率，就是具体的应用例子.

图2 波段辐射出射度计算区域

图3 4980K黑体目标辐射特性计算结果

5 结束语

黑体辐射三大定律及目标辐射体波段辐射出射度的计算问题解决，有助于光电探测系统的优化设计.文中从普朗克辐射公式出发，先运用可视化编程语言对公式作图，然后对Mbλ、λ、T 三者的关系从图像上进行深刻阐述，不仅较为直观地建立了普朗克辐射公式和维恩位移定律、斯忒藩－玻尔兹曼定律之间的联系，而且进一步加深了对三个定律物理意义的理解.特别是从图形出发，运用数值计算方法，求解得到工程实践中所关心的某一温度下某一波段λ1～λ2范围内的辐射出射度Mλ1～λ2.将上述科研工作的思路在课堂教学时非常明白地告知学生，这对激发学生学习兴趣、引导学生深刻领会所学知识、灵活在工程中运用所学知识，拓展学生的创新思维都是大有裨益的.

［1］金伟其，胡威捷.辐射度 光度与色度及其测量［M］.北京：北京理工大学出版社，2009.36～39

［2］肖辉，汪镭，金立军等.电器照明技术［M］2版.北京：机械工业出版社，2010.28～30

［3］江文杰，曾学文，施建华.光电技术［M］.北京：科学出版社，2009.51～54

［4］张兆礼，赵春晖，梅晓丹.现代图像处理技术及Matlab实现［M］.北京：人民邮电出版社，2001

［5］徐代升，陶家友，陈松.基于Matlab的黑体辐射特性分析［J］.湖南理工学院学报，2008，21（4）：35～38

［6］朱焕文，刘贤诗，郑亲波等.黑体辐射数据表［M］.北京：科学出版社，1984

［7］徐代升，贾明，朱华杰等.目标热辐射特性的可视化计算［J］.大气与环境光学学报，2007，2（4）：284～289