基于分离粒子随机扩散理论的色谱模拟

郭 彦 傅应强 孙寅璐 陈天南 赵健伟,*

(1南京信息工程大学环境科学与工程学院,江苏省大气环境监测与污染控制高技术研究重点实验室,南京210044; 2南京大学化学化工学院,生命分析化学国家重点实验室,南京210093)

1 引言

分子扩散,尤其是在微纳米尺度受限空间内的分子扩散是化学学科中的核心问题之一,微化学反应器、分子筛催化、晶体生长、分离富集等基本化学过程都与之密切相关.1-6分子扩散行为对于这些化学过程中产物的组成和分布具有决定作用.了解该过程对提升器件性能、优化操作以及新型反应器件的设计等都尤为关键.对分子扩散行为的研究,除了利用一些先进的实验方法外,随着计算技术的进步,模拟仿真也成为有力的研究手段.计算机模拟在研究分子扩散过程中有显著的优势,它可以从微观模拟每个粒子的扩散行为,动态追踪并显示扩散过程,分析各种环境因素对扩散行为的影响,了解不同操作条件下的扩散机制,进而解释实验中所观察到的现象,为实验化学提供微观理论基础.

分子动力学在描述微观扩散行为方面具有独特的优势,7,8但其计算工作量巨大,现有的计算技术水平还不能为模拟较大的扩散体系提供软硬件支撑.而随机行走的优势在于提取了制约扩散行为的关键信息,对该行为进行了合理近似,从而有效简化了计算工作量,使从微观角度模拟分离扩散成为可能.随机行走模型已在一些扩散问题的研究中得到较为广泛的应用,如土壤介质、生物组织、药物输运、神经元传导和晶体生长等.9-13

气相色谱以其高灵敏度、高分辨率和高选择性已成为最为常用和重要的分离分析方法.基于宏观的扩散理论,人们对于色谱的保留值规律、峰形规律、色谱条件的优化等已有大量的实验研究.14-16色谱理论的发展,亟需从微观角度对色谱的分离规律以及条件控制开展模拟研究,Siepmann等17应用蒙特卡罗方法模拟了烃类在气液色谱界面上的吸附和分配情况.OʹConnell等18应用格子-偶极模型在介观尺度上模拟了肽链在反相色谱上的吸附行为. Thornton等19应用MM+力场和AM1半经验方法计算了脂肪族和芳香族溶质的范德华半径、与固定相和流动相的相互作用,及这些作用情况在反相色谱分离中的应用.Sun等20应用分子动力学研究了配体密度对于蛋白质在疏水电荷诱导色谱上的吸附、脱附、构象变化的影响.Sarti等21应用数学模型研究了蛋白质在膜亲和相色谱中的吸附平衡和流出曲线.值得注意的是,这些模拟研究尽管对色谱的吸附热力学、待分离物质的物性以及溶剂化环境等作了较为深入的研究,但尚未涉及到色谱动力学的内容,如追踪每个分离粒子的运动轨迹,验证速率理论方程和流出曲线方程,研究粒子在色谱柱内分布平衡和迁移过程等.这些动力学方面的研究将有助于进一步了解色谱的分离本质,提升分离器件性能和优化分离条件.

气相色谱中分子扩散既有随机运动特征,又受限于微尺度空间的具体环境.基于这两个特点,本文采用粒子在排布周期性势垒的二维空间中随机行走的方法模拟了色谱中粒子的扩散行为,利用粒子与势垒的弹性碰撞简化了色谱中待分离粒子与固定相之间的相互作用.重点考察了固定相的填充率、固定相的形状和柱长因素对色谱动力学行为的影响.

2 模拟与计算方法

采用自行开发的随机行走软件,22,23对色谱填充柱中粒子扩散过程进行模拟(如图1所示):粒子在给定的初速度条件下在二维受限空间内按照随机的方式运动,在预设时间后粒子运动停止,根据给定的条件计算粒子的运动轨迹并分析粒子的运动行为.

2.1 分离柱

图1 算法模型示意图Fig.1 Schematic diagram of the simulated modelThe tetragonal region,the blank area,the dashed box,the dot,and the curve represent the stationary phase,the cavity,the cell, the particle,and its trajectory,respectively.

分离柱定义为二维平面空间,该空间在x方向上无限延伸,y方向上有上下两个边界.空间内周期排布着单元格,如图1b中的虚线框所示.单元格中的多边形为势垒,用来模拟色谱中的固定相,如图1b中的正方形所示,势垒粒径为正方形对角线长度.用势垒面积除以单元格面积可以求出势垒填充率.二维空间内粒子可以在空腔内(无势垒区域)自由运动但不能进入这些势垒.基于色谱分离的特点,其热力学和动力学过程都发生在曲线流出方向,也就是色谱可以近似看成为一维体系,因而本模拟主要关注粒子扩散的x方向.如无特别说明,分离柱均是长度为1 m的填充柱.

2.2 分离物

以忽略质量和体积的粒子作为分离物,如图1b中的圆点所示.粒子的位置用其所在单元格当中的相对于单元格中心点的相对位置来描述:

其中,Parrel是粒子的相对位置对应的位矢,Parabs是粒子的绝对位置对应的位矢,Cellabs是单元格中心点的绝对位置对应的位矢.在预设时间后,粒子在二维平面空间内的运动完全停止,即相对于所在单元格的绝对位置不再发生变化.

粒子的速度由两部分组成.一是粒子的扩散速度,该速度为温度相关的一个变量.模拟中温度采用室温298 K,根据气体布朗运动估算,粒子的扩散速度设定为2×10-3m·s-1.粒子扩散的运动方向随机生成,在以粒子为中心的0≤α＜2π范围内等概率分布,α为方向角.当粒子达到色谱边界上时,将按照弹性碰撞模型,即粒子的扩散速度大小不变,方向按照反射定律进行反射后继续在色谱柱中运动.

另一个速度为给待分离粒子施加的横向速度,用来模拟载气流速,在程序中定义为沿x轴方向的线速度(Vx,单位为mm·s-1).

2.3 扩散过程

粒子和势垒的相互作用可以用多种模型来描述,本模拟中采用弹性碰撞模型简化了粒子与固定相的作用.假定粒子在某段时间之内速度的方向和大小不发生变化,即速度和时间步(即粒子的实际行走物理单位与在模拟程序中的时间单位之间的比值,程序中采用0.005 s·step-1)决定了粒子一步随机行走的步长;在不受到势垒阻碍的情况下,根据速度、每步时间和粒子的当前位置即可确定粒子完成一步行走之后所处的位置.若粒子与势垒发生碰撞,则可计算出粒子运动到碰撞点所需要的运动时间,将当前时间减去运动时间更新当前时间,将速度按照反射定律进行反射,据此可以确定碰撞之后的粒子运动轨迹.根据粒子若干个时间段内位置参数的时间积分,即可以确定整个时间段内粒子运动的轨迹,如图1c所示.

3 结果与讨论

应用如上描述的模拟程序,研究了气相色谱中待分离粒子在固定相中的扩散行为.重点考察了固定相的填充率、固定相的形状和柱长等结构特性因素对于色谱动力学行为的影响.

3.1 固定相的填充率

固定相填充质量的优劣直接影响到色谱填充柱的分离效果,在模拟程序中势垒填充率大小可以反映出色谱中固定相的填充情况.在周期单元一定的条件下,势垒粒径设置小,则填充率小,相当于一般实验经验中采用固定相填充的较为疏松的色谱柱;势垒粒径大,填充率大,相当于固定相填料粒度小,填充的紧实.模拟中势垒粒径大小分别设置为0.80、0.84、0.88、0.92、0.96和0.98 mm,相对应的填充率为32%、35%、39%、42%、46%和48%,考察粒子在500 s时间内的扩散行为.图2给出了相同的载气流速(Vx=2 mm·s-1)条件下,随着势垒粒径的变化,粒子沿x轴向扩散的统计分布图.每个粒径条件下的柱状图都分别为1000个粒子扩散的统计结果.图中曲线为对统计数据点的拟合曲线,由图可见,在所设定的填充率下,粒子在柱内x轴向上的浓度分布符合高斯正态分布,峰形对称性好,与实际色谱中粒子的扩散行为非常吻合.当势垒粒径从0.80增大到0.98 mm,相当于固定相填料粒度由大变小,图2显示峰形逐渐变窄变尖锐,柱效增加,同时峰的中心位置即粒子在柱内x轴向上浓度分布的平均距离减小.

图2 相同载气流速(Vx=2 mm·s-1)条件下,粒子在预定时间(500 s)内沿x轴向扩散随势垒粒径(0.80、0.84、0.88、0.92、0.96和0.98 mm)变化的统计分布图Fig.2 Statistical distribution graph of the x axial distances passed by the particles(500 s)with the barrier sizes(0.80, 0.84,0.88,0.92,0.96,and 0.98 mm)under the fixed carrier gas flow rate(Vx=2 mm·s-1)

半峰宽是色谱分离流出曲线的一项重要参数,涉及到色谱动力学和组分分离方程.图2中统计峰的半峰宽随着势垒粒径的增大,总体变化趋势是在减小,说明柱效有增大趋势.我们也系统考察了在其它载气流速下,相应的半峰宽特征,均表现为随势垒粒径的增大而减小,而在相同粒径条件下,不同载气流速对半峰宽基本没有影响.色谱柱参数中,固定相的填充情况可以用涡流扩散项A来描述:24

上式中,λ为填充不均匀性因子,随机行走模拟中,势垒都是以相同的密堆方式堆积,因而势垒粒径的改变对λ的影响可以忽略.dp为填料粒径,当设置的势垒粒径变大时,对应于一般实际实验时使用了小颗粒的填料,填充得紧实密集,使得粒子在扩散中迁移路径较为接近.由经典的van Deemter方程可知dp的减小将导致塔板高度变小,柱效提高,半峰宽减小.在固定相填充率与色谱柱效研究方面,该模拟结果与一般实验经验一致.

图3 在不同的载气流速条件(Vx=4,2,1 mm·s-1)下,粒子在预定时间(500 s)内x轴向扩散平均距离随势垒粒径(0.80、0.84、0.88、0.92、0.96和0.98 mm)变化的关系图Fig.3 Mean x axial distances passed(500 s)versus the barrier particle sizes(0.80,0.84,0.88,0.92,0.96,and 0.98 mm)under fixed carrier gas flow rates(Vx=4,2,1 mm·s-1)

势垒粒径对粒子扩散行为的影响还体现在粒子在x轴向上的扩散,也就是粒子在x轴向上的浓度分布,实质上描述了粒子的色谱流出曲线.图3为在不同的压力条件,即不同载气流速(Vx分别为4、2和1 mm·s-1)下粒子在预定时间(500 s)内在x轴向扩散距离的平均值与势垒粒径大小的关系图.由图可知,在相同压力条件下,势垒粒径越小,粒子沿x轴向扩散距离越大,对应于色谱中使用大粒径的填料,填充率减小,粒子在扩散时与固定相的碰撞作用减少,粒子可以沿相对较直的路径较快地通过色谱柱.在相同势垒粒径条件下,载气流速越大,粒子的轴向扩散距离越大,相当于在实验过程中增加了轴向驱动力,粒子的流动行为更加越明显.Darcy法则给出对于粒径较小的填料,可以观察到流动相线速度与粒径平方的线性关系,由于模拟条件设定粒径相对较大,相同时间下的轴向距离与势垒粒径呈一元回归响应.

粒子位移平方的平均值称为均方位移(MSD),是用来表征粒子运动性质的微观物理量.在模拟程序中定义为

其中N是总步数,dk表示粒子在k步后的位置矢量(d0是初始位置),|dk+t-dk|表示k步到k+t步的位移矢量.

图4为在相同的载气流速(Vx=2 mm·s-1)条件下,填充物粒径大小从0.80增大到0.98 mm时MSD变化图.由图可见,当填充物粒径较大时,MSD随时间线性变化,表明粒子的运动行为为自由扩散过程,由斜率可以求出扩散系数.如势垒粒径为0.96 mm时,扩散系数为0.049 mm2·s-1,这个值比实际气体扩散系数略大.25,26当势垒粒径减小,MSD随时间呈曲线变化,表明粒子除了在固定相中有扩散行为,还有明显的流动行为,27该流动行为的驱动力来自于外加载气压力和固定相对粒子扩散阻力的综合作用.因而势垒粒径越小,流动行为越明显,这也与图3的结果相一致.

图4 相同载气流速(Vx=2 mm·s-1)条件下,不同势垒粒径大小(0.80、0.84、0.88、0.92、0.96和0.98 mm)的均方位移(MSD)Fig.4 Mean square displacement(MSD)of several barrier particle sizes(0.80,0.84,0.88,0.92,0.96,and 0.98 mm)with the fixed carrier gas flow rate(Vx=2 mm·s-1)

3.2 固定相的形状

本文也考察了固定相填料的形状(势垒从四边形到接近圆形的二十边形)对色谱的影响,模拟结果如图5插图所示.图中尽管固定相形状不同,但粒子扩散的峰形和浓度分布的平均距离都非常接近,表明在模拟中固定相形状对粒子的扩散行为并没有明显的影响.在一般色谱实验经验中,色谱柱采用圆形填料,是由于圆形填料更容易填充紧实,在模拟中,由于固定相都是以预设的密集方式排布,因而形状影响没有实际中重要.

不同固定相形状对应的半峰宽也都在0.2 m左右的范围内波动,如图5所示,也说明密集排布的固定相形貌对粒子的扩散行为影响不大,但要注意到,当固定相填料形状开始接近于圆形如十二、十六和二十边形时,半峰宽略有变小,相应于在固定相密集排布的基础上,填充的不均匀性因子λ减小也起到了一定作用,使得柱效略有增加.

尽管本文对色谱模拟条件进行了适当的简化,这种固定相排布相同但形状不同对分子扩散微弱的影响,为有些如载体相同固定液不同且分离效果相近的实际实验,提供了部分理论支持.28,29

3.3 柱 长

图5 半峰宽与势垒形状的关系图Fig.5 Relation between FWHM and the barrier shapesThe inset is statistical distribution graph of the x axial distances (500 s)with the barrier shapes(polygon n=4,6,8,12,16,20)under the fixed carrier gas flow rate(Vx=2 mm·s-1)and barrier particle size(0.88 mm).FWHM:full width at half maximum

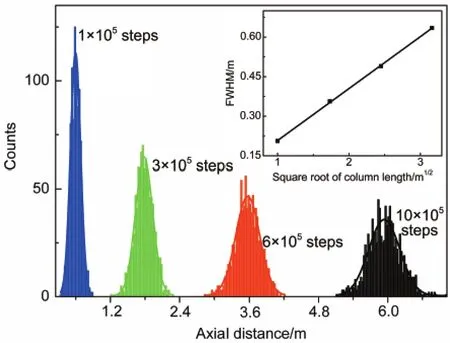
图6 给定载气流速(Vx=2 mm·s-1)和固定相粒径大小(0.88 mm),固定相形状(四边形),粒子沿x轴向扩散随分离时间(500、1500、3000和5000 s)变化的统计分布图Fig.6 Statistical distribution graph of the x axial distances with the different of calculation times(500,1500,3000 and 5000 s)under the fixed carrier gas flow rate(Vx=2 mm·s-1), barrier size(0.88 mm)and barrier shape(tetragon) Inset is the FWHM versus square root of column length.

进一步考察了柱长对粒子分离扩散的影响.图6为在相同的载气流速下(Vx=2 mm·s-1),相同的固定相填充率及固定相形状条件下,通过计算步长的增加(1×105、3×105、6×105和10×105步),即在分离时间分别为500、1500、3000和5000 s时考察粒子的扩散行为.在设定的分离时间条件下,相当于色谱柱长分别为1、3、6和10 m.由图6可以看出,分离时间设定越长,即柱长越长,粒子的浓度分布峰越钝越宽.理想的气相色谱通常满足以下条件:色谱柱内任何点上两相的比例恒定;载气流在色谱柱内任何部位均一样;在两相中均不发生分子的纵向扩散作用;组分分子的分配平衡能瞬间完成.30一般的实验经验中,通常分子的纵向扩散和分配平衡是峰展宽的决定因素.本模拟中,为了能够追踪粒子的扩散过程,简化了粒子与固定相的作用,因而峰展宽的主要因素为粒子的纵向扩散.图6中柱长越长,在相同起点上的粒子由于纵向扩散作用,使得峰展宽严重.图6插图为图6中粒子浓度分布峰的半峰宽随柱长平方根的变化图,两者呈线性变化,符合色谱流出曲线及质量平衡规律.随着柱长的增加,半峰宽指数级的增大,相应于柱效变差,这也为在达到完全分离前提下尽量用短柱的实验经验,提供了可靠的模拟基础.

4 结论

利用随机行走的算法对气相色谱中粒子在固定相中的扩散行为进行了模拟,模拟了粒子扩散的运动轨迹和流出曲线,流出曲线均呈高斯分布,与实际色谱粒子的扩散过程一致.文中重点考察了固定相的填充情况、固定相的形状和柱长等性能指标对粒子扩散行为的影响,模拟结果表明固定相填充情况和柱长对色谱出峰的影响与实际经验相符,而在相同的密堆排列下,固定相形状基本对色谱动力学无明显影响.

(1) Grill,L.;Dyer,M.;Lafferentz,L.;Persson,M.;Peters,M.V.; Hecht,S.Nat.Nanotechnol.2007,2,687.doi:10.1038/ nnano.2007.346

(2)Yariv,E.;Ben-Dov,G.;Dorfman,K.D.Europhys.Lett.2005, 71(6),1008.doi:10.1209/epl/i2005-10171-6

(3) Corma,A.;Díaz-Cabañas,M.J.;Jordá,J.L.;Martínez,C.; Moliner,M.Nature 2006,443,842.doi:10.1038/nature05238

(4) Ridgway,D.;Broderick,G.;Lopez-Campistrous,A.;Ruaini, M.;Winter,P.;Hamilton,M.;Boulanger,P.;Kovalenko,A.; Ellison,M.J.Biophys.J.2008,94(10),3748.doi:10.1529/ biophysj.107.116053

(5) Persson,A.I.;Larsson,M.W.;Stenström,S.;Ohlsson,B.J.; Samuelson,L.;Wallenberg,L.R.Nat.Mater.2004,3,677.doi: 10.1038/nmat1220

(6) Chou,C.F.;Bakajin,O.;Turner,S.W.P.;Duke,T.A.J.;Chan, S.S.;Cox,E.C.;Craighead,H.G.;Austin,R.H.Proc.Natl. Acad.Sci.U.S.A.1999,96(23),13762.

(7)Wang,F.Y.;Liu,Y.H.;Yin,X.;Wang,N.;Wang,D.X.;Gao,Y. J.;Zhao,J.W.J.Appl.Phys.2010,108,074311.doi:10.1063/ 1.3477323

(8)Liu,Y.H.;Zhao,J.W.;Wang,F.Y.Phys.Rev.B 2009,80, 1154117.

(9) Rao,P.S.C.;Jessup,R.E.;Addiscott,T.M.Soil Sci.1982,133, 342.doi:10.1097/00010694-198206000-00002

(10) Safford,R.E.;Bassingthwaighte,E.A.;Bassingthwaighte,J.B. J.Gen.Physiol.1978,72,513.doi:10.1085/jgp.72.4.513

(11) Santamaria,F.;Wils,S.;De Schutter,E.;Augustine,G.J. Neuron 2006,52,635.doi:10.1016/j.neuron.2006.10.025

(12) Saltzman,W.M.Drug Delivery:Engineering Principles for Drug Therapy;Oxford University Press:New York,2001;pp 1-30.

(13) Zubarev,E.R.;Pralle,M.U.;Li,L.;Stupp,S.I.Science 1999, 283,523.doi:10.1126/science.283.5401.523

(14)McNair,H.M.;Miller,J.M.Basic Gas Chromatography;John Wiley&Sons:Hoboken,New Jersey,2009;pp 1-267.

(15) Poole,C.F.The Essence of Chromatography;Elsevier Science B.V.:Amsterdam,the Netherlands,2003;pp 80-86.

(16) Heftmann,E.Fundamentals and Applications of Chromatography and Related Differential Migration Methods, in Chromatography;Elsevier Science B.V.:Amsterdam,the Netherlands,2004;pp 319-364.

(17)Wick,C.D.;Siepmann,J.I.;Schure,M.R.Anal.Chem.2002, 74,3518.doi:10.1021/ac0200116

(18) Makrodimitris,K.;Fernandez,E.J.;Woolf,T.B.;OʹConnell,J. P.Anal.Chem.2005,77,1243.doi:10.1021/ac048812r

(19)Turowski,M.;Yamakawa,N.;Meller,J.;Kimata,K.;Ikegami, T.;Hosoya,K.;Tanaka,N.;Thornton,E.R.J.Am.Chem.Soc 2003,125,13836.doi:10.1021/ja036006g

(20) Zhang,L.;Zhao,G.;Sun,Y.J.Phys.Chem.B 2010,114,2203. doi:10.1021/jp903852c

(21) Dimartino,S.;Boi,C.;Sarti,G.C.J.Chromatogr.A 2011,1218, 1677.doi:10.1016/j.chroma.2010.11.056

(22) Fu,Y.;Chen,L.;Ke,J.;Gao,Y.;Zhang,S.;Li,S.;Chen,T.; Zhao,J.Mol.Simul.2012,38(6),491.doi:10.1080/ 08927022.2011.649427

(23) Ke,J.Y.;Fu,Y.Q.;Chen,L.L.;Chen,T.N.;Zhang,S.J.; Wang,H.B.;Zhao,J.W.J.Fudan Univ.2012,51(2),251. [柯佳颖,傅应强,陈莉莉,陈天南,张世界,王洪波,赵健伟.复旦大学学报,2012,51(2),251.]

(24) van Deemter,J.J.;Zuiderweg,F.J.;Klinkenberg,A.Chem. Eng.Sci.1956,5,271.doi:10.1016/0009-2509(56)80003-1

(25) Schwander,J.;Stauffer,B.;Sigg,A.Ann.Glac.1988,10,141.

(26) McAfee,M.;Lindström,J.;Johansson,W.J.Soil.Sci.1989,40 (4),707.doi:10.1111/ejs.1989.40.issue-4

(27) Saxton,M.J.;Jacobson,K.Annu.Rev.Biophys.Biomol.Struct. 1997,26,373.doi:10.1146/annurev.biophys.26.1.373

(28) Sander,L.C.;Wise,S.A.Anal.Chem.1995,67(18),3284.doi: 10.1021/ac00114a027

(29) Welsch,T.;Michalke,D.J.Chromatogr.A 2003,1000,935.doi: 10.1016/S0021-9673(03)00503-X

(30)Keulemans,A.L.M.;Kwantes,A.Vapour Phase Chromatography;Academic Press:New York,1957;p 15.