表面电荷及外电场对液固界面热阻的影响

葛 宋 陈 民

(清华大学工程力学系,北京100084)

1 引言

当热流流过液固界面时,界面处会存在温度的不连续.这种温度的不连续是由液固两相间的界面热阻所引起.液固界面热阻由Kapitza在1941年首先发现,因此也被称为Kapitza热阻.1在常规条件下,界面热阻往往可以忽略.但是近年来,随着微纳米技术的发展,界面热阻由于其在微纳米尺度热传递现象中的相对重要性而受到越来越多学者的关注.2界面热阻的影响可由热阻长度来衡量.3实验测量和分子模拟的结果都表明,在液固相互作用较弱的界面,热阻长度可达数十纳米.4,5因而,在微纳米系统及含有大量液固界面的体系(如纳米流体)中,界面热阻均不可忽略.

使固体表面带电荷及施加外电场是改变液固界面性质的有效手段,有着广泛的应用前景.6-13朱素华等6的分子动力学模拟研究显示,外电场会影响水分子在膜材料中的电渗迁移运动.李海兰等7对不同电量修饰的碳纳米管中水分子行为的模拟表明电荷对水分子的密度分布和扩散速率以及水通量有显著影响.在微纳机电系统中,通常通过外加电场和通道表面的电荷来驱动微通道内液体流动.8Powell等9的研究显示电场可以控制水分子在纳米孔中的通过与阻断.此外,通过调整施加在液体/固体间的电势来改变两者间接触角的电润湿现象,10可以实现液体在表面上亲水与疏水的可逆转换,在显示技术及微液滴操控和流动控制等领域有广泛的应用.11-13表面电荷和电场能改变界面以及水分子体系本身的一些性质,14,15有可能对液固界面间的能量输运产生影响.Lee等16的研究表明纳米颗粒的表面电荷对纳米流体的导热系数有重要影响,并认为表面电荷能增强液固间的热输运.但目前对于表面电荷和电场对界面热阻的影响还没有直接的报道.本文利用分子动力学方法模拟了固体表面电荷和外加电场对水与固体间界面热阻的影响,在加深对界面热阻影响机制理解的同时,也能为实际应用提供有益参考.

2 模拟方法与细节

本文所有模拟都采用了分子动力学模拟软件Large-Scale Atomic/MolecularMassively Parallel Simulator(LAMMPS).17模拟中,水分子采用常用的extended simple point charge(SPC/E)模型.18,19水分子间的相互作用可表述为

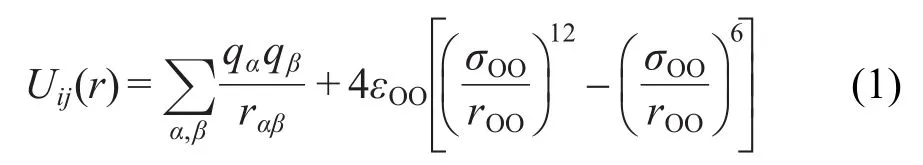
式(1)中前半部分为电荷间的静电作用,后半部分为氧原子间的Lennard-Jones(LJ)作用.其中qα、qβ分别表示不同水分子中的点电荷,rαβ为两电荷间的距离. εOO、σOO分别表示氧原子间LJ作用的能量参数和长度参数,rOO为氧原子间的距离.固定SPC/E水分子模型假设只有氧原子间存在LJ作用,且水分子的构型在模拟中保持不变,即键长和键角固定.固体采用以铜为原型的LJ固体,其势能参数为ε=6.64× 10-20J,σ=2.277×10-10m.20固体原子按面心立方(face-centered cubic)结构排列,晶格常数取a0= 1.56σ.21由于LJ固体熔点正比于能量参数ε,在本文模拟的温度下此模型能很好地维持固体状态而无需人为引入弹簧力来维持,并且能很好地描述固体的热学性质.5水分子与固体间的相互作用由氧原子与固体原子间的LJ势来描述,势能参数εSO=2.78× 10-21J,σSO=(σOO+σSS)/2＝2.782×10-10m.

液固界面热阻的模拟体系如图1所示,由液体区域和固体区域两部分构成.模拟盒子的尺寸为15a0×15a0×32a0,其中液体区域尺寸为15a0×15a0× 20a0.水分子的密度设为994 kg·m-3.体系共含有6700个水分子和11700个固体原子.如图1所示,在沿z方向的两端分别设定两个固定的原子层,以维持模拟体系稳定.在紧邻固定原子层的液体和固体图示区域分别设置热源和热沉,以此在体系中形成热流和温度梯度.液体中热源区域和固体中热沉区域的大小均为15a0×15a0×a0.在x和y方向均采用周期性边界条件.模拟中为了提高效率,只有当原子间的距离小于截断半径(1.0 nm)时才计算LJ相互作用.而库仑力为长程相互作用,在本文中采用particle-particle particle-mesh(PPPM)方法22来处理.模拟中采用SHAKE算法23来固定水分子的键长和键角.粒子运动方程的积分采用速度Verlet算法24,积分步长取为0.5 fs.模拟首先采用NVT系综,利用Nose-Hoover控温方法25使体系在300 K下演化50万步,随后将控温移除,使体系在NVE系综中演化.在热源中不断输入热量,在热沉中移走相等的热量,其具体做法是在每一步先通过坐标来确定所有处于热源和热沉中的原子,然后通过重新调整热源和热沉区域中原子的热运动速度来分别输入和移出能量.26体系整体将保持能量守恒.每一步加入和移出热量ΔE,体系中的热流将为J=ΔE/AΔt(其中A为界面的横截面积,Δt为时间步长).此过程持续80万步令体系达到稳定,体系中建立起稳定的温度分布,界面温度跳跃ΔT及热流J.界面温度跳跃ΔT定义为界面处液体层和固体层的温度差.继续计算200万步以完成统计采样.将体系沿z方向划分成条状区域,其厚度为a0,每个条状区域中含有超过300个原子以减小温度统计的涨落.将总的模拟时间分成10个时间块,利用块平均的方法27来确定温度的平均值及误差.统计各区域中的温度可获得温度分布和界面温度跳跃.液固界面热阻RK则可由其定义RK=ΔT/J来获得.

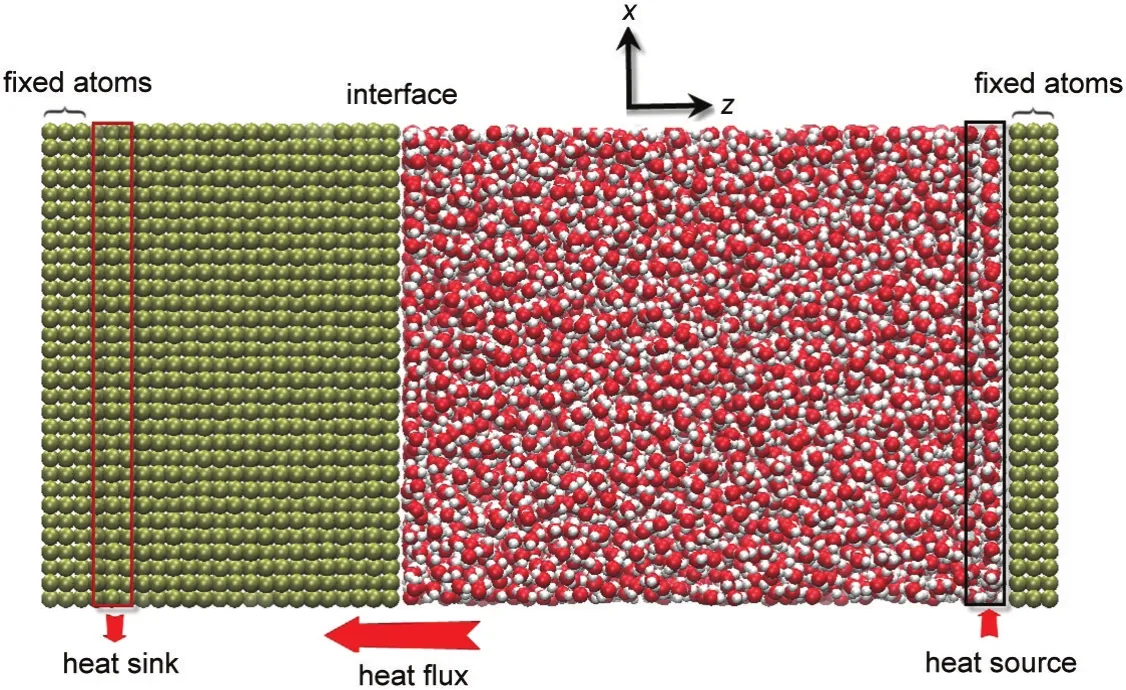
图1 液固界面热阻的模拟体系Fig.1 Simulation system for the liquid/solid interfacial thermal resistance

3 结果与讨论

首先我们讨论无表面电荷和外电场的情况.模拟需要先设定体系的热流密度.设定的热流密度不能太大以保证体系维持在线性响应区域,又要保证能产生足够强的温度信号.Hu等28对水与硅胶界面热阻的模拟结果显示在热流较大(＞6000 MW·m-2)时,界面热阻几乎与设定的热流大小无关.因此本文中采用的热流为J=7350 MW·m-2.稳定后体系内的温度分布如图2所示.在给定的热流密度下,稳定后固体和液体体系内的温度分布均较好地满足线性分布,体系处于线性响应区,傅里叶导热定律仍然成立.可以看到液体中的温度梯度要明显大于固体中的温度梯度,这是由于固体热导率远大于液体热导率.液体与固体在界面处存在显著的温度不连续.由热流密度和界面温度跳跃计算得到固体与水之间的界面热阻RK=3.73×10-9K·m2·W-1,与之相对应的界面热导(界面热阻的倒数)为268 MW·m-2· K-1.此界面热导与Ge等29实验测量得到的水与AuPd双金属纳米粒子间的界面热导(100-300 MW·m-2·K-1)处于同一量级.

图2 稳定后体系内的温度分布Fig.2 Temperature distribution of the system after equilibrium

为考虑固体表面电荷对界面热阻的影响,模拟中设定与水分子接触的最外层原子分别带0.01e-0.05e的正负电荷,对应的表面电荷密度为1.6-8.0 mC·cm-2.体系中除增加了水分子上的电荷与表面电荷间的静电作用外,其它势能均保持不变.图3所示为表面电荷对界面热阻的影响.采用简单的函数形式对此关系进行拟合,发现二次函数能较好地描述表面电荷密度与界面热阻的关系,拟合曲线如图3所示.

可以看到,无论表面带正电荷还是负电荷,界面热阻都随着表面电荷密度的增加而减小.表面电荷可有效减小界面热阻,促进界面处的能量输运.

当考虑外加电场对界面热阻的影响时,由于水分子模型中点电荷的存在,电荷将受到电场力F=qE的作用,其中q为点电荷电量,E为电场强度.我们考虑电场的两种不同布置方式,即垂直于界面与平行于界面,其中垂直于界面还可以分为垂直于界面指向液体和垂直于界面指向固体.为了表述方便,我们将指向液体记为正方向,指向固体记为负方向.图4所示为电场垂直于界面时对界面热阻的影响.同样采用二次函数拟合能较好地描述电场强度与界面热阻的关系,拟合曲线如图4所示.

图3 界面热阻随表面电荷的变化Fig.3 Interfacial thermal resistance as a function of surface charge

由图4可见,电场垂直于界面时,无论电场方向指向液体还是固体,界面热阻都随着电场强度的增加而减小.电场强度与界面热阻的关系也同样能通过二次函数来较好地拟合,电场和表面电荷对界面热阻的影响存在类似的效果.值得一提的是,在电润湿现象中,接触角的余弦与外加电压之间也存在二次函数的关系.10由于界面热阻和表面湿润性间存在一定的联系,30电场和表面电荷对界面热阻和湿润性两种界面现象的影响可能存在相似的机理,还有待进一步探究.

当电场平行于界面方向时界面热阻的变化情况则有所不同.图5所示为电场平行于界面时界面热阻的变化,界面热阻几乎不受外加电场的影响.

图4 电场垂直于界面时界面热阻随电场强度的变化Fig.4 Interfacial thermal resistance as a function of electric field strength when the electric field is perpendicular to the interface

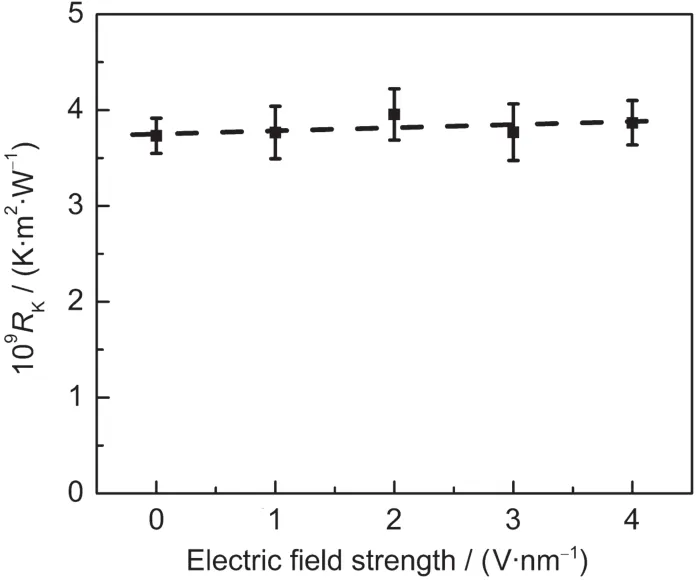
图5 电场平行于界面时界面热阻随电场强度的变化Fig.5 Interfacial thermal resistance as a function of electric field strength when the electric field is parallel to the interface

由上面的结果可以看出通过施加表面电荷和特定方向上的外电场确实可以改变液固间的界面热阻.由于水分子本身带有等量的正负电荷,呈电中性,在外电场或电荷的作用下整体受力为零,因此不会产生水分子在界面处的聚集等现象.在静电力不是非常强的情况下也不会对水分子的整体结构性质(如长程有序度等)产生影响.我们分析不同电场强度下液体水中氧原子的径向分布函数gOO(r) (径向分布函数表征的是距离目标原子为r的球壳内另一种原子的密度与平均密度的比值,其可以反映液体体系的结构特征).如图6所示,电场对氧氧原子的径向分布函数几乎没有产生可见的影响,这也与Evans等14的结论一致.因此可排除界面水分子聚集和长程结构变化的影响.考虑到水分子虽然呈电中性,但由于水分子的结构特征,水分子中存在偶极矩,从而使得水分子的取向会受到表面电荷和外电场的影响.在无表面电荷和外电场的条件下,由于水分子取向的随机排列,水分子体系的平均偶极矩为零,而正负表面电荷或垂直于界面的正负电场将导致水分子垂直于界面向上或向下排列.此现象已得到了模拟的验证,如Evans等14分析了电场作用下水分子的结构,表明水分子会发生沿电场方向的定向排列,平均偶极矩会随电场的增大而增加.考虑液固间能量传递的机理,液体中的能量传递与固体有所不同,由于液体不能承受剪切,液体中的能量传递主要以纵向声波为主.1水分子在电场和表面电荷影响下的排列方式可能会明显增强液体水中的纵向声波的能量输运,从而促进水分子与固体间的能量交换.而平行于界面施加的电场引起的偶极矩排列可能对热量输运不产生明显影响.但其中的机理还有待进一步研究.

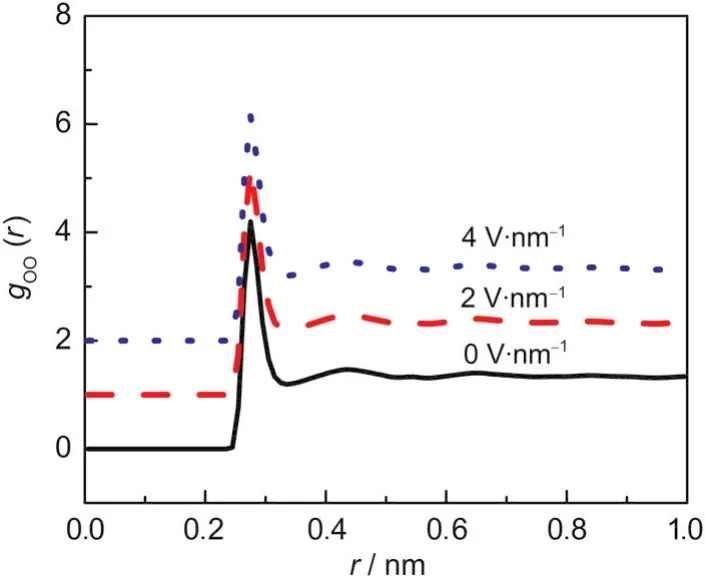
图6 垂直界面施加电场时水分子中氧氧径向分布函数Fig.6 Radial distribution function for oxygen atoms in water when the external electric field is perpendicular to the interface

4 结论

采用非平衡分子动力学模拟分析了固体表面电荷及外电场对水与固体间界面热阻的影响.模拟结果表明,壁面带正电荷或负电荷都将使得界面热阻减小,且界面热阻与表面电荷密度满足二次函数关系;外加电场平行于界面时,其对界面热阻几乎没有产生可见的影响,而垂直于界面时,界面热阻将随着电场强度的增大而减小.界面热阻与电场强度也满足二次函数关系.界面热阻对表面电荷和电场的影响可能与水分子偶极矩的定向排列有关.本文的模拟结果表明改变电场和施加表面电荷是控制界面热阻的有效方法.

(1) Swartz,E.T.;Pohl,R.O.Rev.Mod.Phys.1989,61,605.doi: 10.1103/RevModPhys.61.605

(2)Cahill,D.G.;Ford,W.K.;Goodson,K.E.;Mahan G.D.; Majumdar,A.;Maris,H.J.;Merlin,R.;Phillpot,S.R.J.Appl. Phys.2003,93,793.doi:10.1063/1.1524305

(3) Barrat,J.L.;Chiaruttini,F.Mol.Phys.2003,101,1605.doi: 10.1080/0026897031000068578

(4) Ge,Z.B.;Cahill,D.G.;Braun,V.Phys.Rev.Lett.2006,96, 186101.doi:10.1103/PhysRevLett.96.186101

(5) Xue,L.;Keblinski,P.;Phillipot,S.R.;Choi,S.U.S.;Eastman, J.A.J.Chem.Phys.2003,118,337.doi:10.1063/1.1525806

(6) Zhu,S.H.;Yan,L.M.;Ji,X.B.;Shao,C.L.;Lu,W.C.Acta Phys.-Chim.Sin.2010,26,2659. [朱素华,严六明,纪晓波,邵长乐,陆文聪.物理化学学报,2010,26,2659.]doi:10.3866/ PKU.WHXB20100934

(7) Li,H.L.;Jia,Y.X.;Hu,Y.D.Acta Phys.-Chim.Sin.2012,28, 573.[李海兰,贾玉香,胡仰栋.物理化学学报,2012,28, 573.]doi:10.3866/PKU.WHXB201112191

(8) Li,Q.L.;Chen,L.X.Prog.Chem.2008,20,1406.[李清岭,陈令新.化学进展,2008,20,1406.]

(9) Powell,M.R.;Cleary,L.;Davenport,M.;Shea,K.J.;Siwy,Z. S.Nat.Nanotech.2011,6,798.doi:10.1038/nnano.2011.189

(10) Mugele,F.;Baret,J.C.J.Phys.:Condes.Matter 2005,17,R705.

(11) Hayes,R.A.;Feenstra,B.J.Nature 2003,425,383.doi: 10.1038/nature01988

(12) Bhushan,B.;Pan,Y.Langmuir 2011,27,9425.

(13) Wang,Y.L.;Bhushan,B.Langmuir 2010,26,4013.doi: 10.1021/la903460a

(14) Evans,W.;Fish,J.;Keblinski,P.J.Chem.Phys.2007,126, 154504.doi:10.1063/1.2723071

(15) Xu,G.L.;Xiao,X.H.;Liu,Y.F.;Sun,J.F.;Zhu,Z.H.Acta Phys.-Chim.Sin.2007,23,746. [徐国亮,肖小红,刘玉芳,孙金锋,朱正和.物理化学学报,2007,23,746.]doi:10.3866/ PKU.WHXB20070524

(16)Lee,D.;Kim,J.W.;Kim,B.G.J.Phys.Chem.B 2006,110, 4323.doi:10.1021/jp057225m

(17) Plimpton,S.J.Comp.Phys.1995,117,1.doi:10.1006/jcph. 1995.1039

(18)Ge,S.;Zhang,X.X.;Chen,M.J.Chem.Eng.Data 2011,56, 1299.doi:10.1021/je101138g

(19) Ge,S.;Zhang,X.X.;Chen,M.Int.J.Thermophys.2010,31, 2176.doi:10.1007/s10765-010-0863-0

(20)Agrawal,P.M.;Rice,B.M.;Thompson,D.L.Surf.Sci.2002, 515,21.doi:10.1016/S0039-6028(02)01916-7

(21) Chen,G.Nanoscale Energy Transport and Conversion;Oxford University Press:New York,2005;pp 85-86.

(22) Deserno,M.;Holm,C.J.Chem.Phys.1998,109(18),7678. doi:10.1063/1.477414

(23) Ryckaert,J.P.;Ciccotti,G.;Berendsen,H.J.C.J.Comp.Phys. 1977,23,327.

(24)Allen,M.P.;Tildesley,D.J.Computer Simulation of Liquids; Clarendon Press:Oxford,1997;pp 87-89.

(25) Evans,D.J.;Holian,B.L.J.Chem.Phys.1985,83(8),4069. doi:10.1063/1.449071

(26) Jund,P.;Jullien,R.Phys.Rev.B 1999,59(21),13707.doi: 10.1103/PhysRevB.59.13707

(27) Frenkel,D.;Smit,B.Understanding Molecular Simulation: From Algorithms to Application;Academic Press:New York, 1996;pp 529-532.

(28) Hu,M.;Goicochea,J.V.;Michel,B.;Poulikakos,D.Appl.Phys. Lett.2009,95,151903.doi:10.1063/1.3247882

(29) Ge,Z.B.;Cahill,D.G.;Braun,P.V.J.Phys.Chem.B 2004, 108,18870.doi:10.1021/jp048375k

(30) Shenogina,N.;Godawat,R.;Keblinski,P.;Garde,S.Phys.Rev. Lett.2009,102,156101.doi:10.1103/PhysRevLett.102.156101