风场环境下主动建模无人直升机改进LQG控制

李一波，刘婉竹，宋崎，2，赵树

(1.沈阳航空航天大学自动化学院，辽宁沈阳 110136;2.沈阳自动化研究所第一研究室，辽宁沈阳 110016;3.中航工业西安飞机工业(集团)有限责任公司 第31厂，陕西 西安 710089)

引言

无论是高大建筑物的屋顶平台，还是高山峡谷的狭小平地，小型无人直升机均能起降自如，实施多种作业。这样一来就使得执行任务的环境信息常常是不完全透明的，文献［1］把这种信息不完全透明的环境称作不确定环境。目前国内外对于无人直升机飞行控制系统的研究，尤其是对于不确定环境下的研究还不是很充分，主要有以下几种［2］:(1)用特征结构配置法;(2)定量反馈理论(QFT);(3)H∞控制;(4)线性二次型高斯/传递回路恢复(LQG/LTR)方法。LQG方法是用来处理有随机噪声干扰或模型状态无法直接测量情况下的状态反馈最优化设计方法［3］，其本质是附带卡尔曼滤波器的最优二次型控制器。由于传统的LQG控制方法只能对模型中的状态进行估计，而主动建模技术可以对模型中的参数和状态进行在线估计［4］，因此本文将主动建模技术与传统的LQG控制相结合，为系统实时地建立相对准确的模型。

本文所考虑的不确定环境主要指风场环境。在飞行控制系统设计中，大气扰动的各种参数(如风速、风向等)是变化的，当风速非常大，与飞行器的飞行速度接近一个数量级时，大气扰动不能再被看作小扰动事件，为了对飞行器进行有效控制，需要获知大气扰动的模型。大气扰动表现为变化风，其对飞行器的影响主要有风切变和大气紊流［5］。其中大气紊流是一种随机现象，通过抑制紊流干扰改善飞行品质，提高飞行器性能。

目前大气紊流模型有Dryden模型和Von Karman模型，但二者的建模理论体系却截然相反［6］。本文采用改进的Von Karman模型，即对该模型进行有理化逼近，直接基于简化的模型生成大气紊流。

1 直升机半解耦模型的建立

直升机的全状态空间模型包括直升机的刚体动力学模型、旋翼和机身耦合模型、旋翼稳定杆的耦合模型、航向增稳回路模型［7］。

由于直升机全状态空间模型含有耦合参数，且有13个状态量和4个控制输入量，为了简化计算和便于稳定性分析，将纵向和横向的耦合参数设为零，并加入一些自由控制参数以补偿耦合动力学模型，这样得到半解耦之后的3个运动方程:纵向运动方程、横向运动方程和航向运动方程［8］。表达式如下:

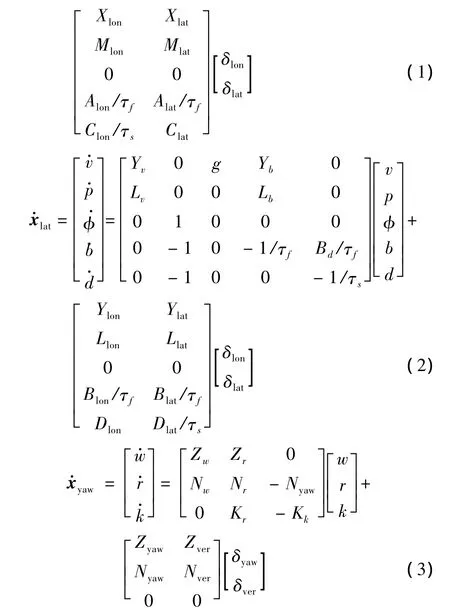
2 风场模型的建立

2.1 大气紊流的模型

自然界中的风从来不以纯净的形式出现，由于摩擦、旋涡等原因，在风出现的同时，也往往伴有紊流。大气紊流现象的形式和出现与很多因素有关，例如风切变、热交换、地形诱导等。大气紊流可以看作是叠加在常值风上的连续随机脉冲。通常认为紊流是一种平稳、均匀、各态遍历及各向同性的随机过程。该过程的统计特性不随时间变化。由于Von Karman模型的使用较广泛，所以本节针对该模型进行介绍。

Von Karman模型的能量频谱函数为:

2.2 数值仿真实现

由于得到的Von Karman模型在飞行仿真实验中不能直接使用，所以首先进行共轭分解，而后使用有理化的方法将其简化，形式如下:

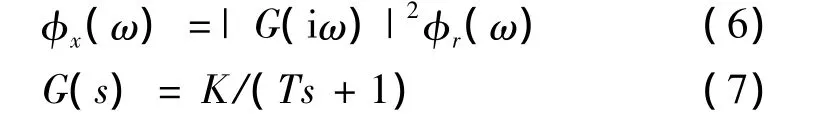
用简化后的Von Karman模型进行数值仿真时，将计算机产生的随机信号作为输入端的信号源，而后将其送入到已按给定频谱设计好的滤波器中，在线实时生成仿真中所需要的大气紊流数据。本文通过计算机产生的随机信号是均值为零、方差为1的高斯白噪声。

在计算机仿真中所用到的递推公式为:

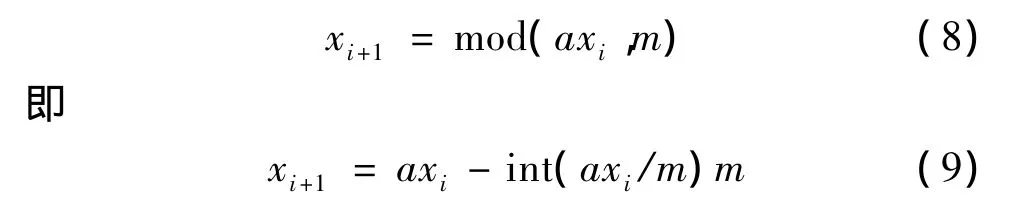
在飞行实时仿真中，以h为步长(即采样周期)将成形滤波器的传递函数G(s)离散化，生成x(t)离散序列的欧拉前差分公式为［9］:

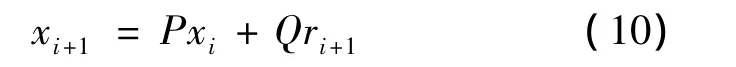
式中，xi为离散序列x第i点的值，即当t=ih时的x值;ri+1为高斯白噪声序列;P和Q与采样周期有关，为待定系数。

按式(10)不断递推产生大气紊流随机信号x(t)，从而实现在线实时仿真。

3 基于主动建模的改进LQG控制

3.1 LQG控制

3.1.1 LQG 介绍

LQG控制方法采用卡尔曼滤波估计状态，并采用线性二次型控制器来设计反馈调节器，它常用来处理有随机噪声干扰存在的或模型状态无法直接测量的控制系统，这样能够保证系统的鲁棒性能。

一个典型的LQG控制系统如图1所示，其中控制器Gc就包含了待设计的卡尔曼滤波器和二次型补偿器。

图1 典型的LQG控制系统

3.1.2 LQG 设计

设控制系统的方程有如下表达式:

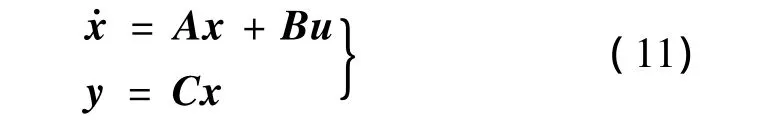
式中，x为飞行器的状态量;u为控制输入量。如果用z表示期望输出量，则误差量可表示为:

LQR的设计方法可描述为:首先确定飞行器期望的时域性能指标，并以二次型的形式定义状态调节性能指标J，即:

设计反馈调节器K，使式(12)最小，并保证所用的控制能量以及飞行器状态的振荡最小。

3.1.3卡尔曼滤波

为了克服数据无法处理的问题，20世纪60年代卡尔曼将状态空间模型引入到滤波理论中，推导出了一套递推估计算法，后人称之为“卡尔曼滤波理论”。卡尔曼滤波器采用含有噪声的系统信号状态空间模型，利用当前时刻的观测值和上一时刻的估计值来更新对状态变量的估计，从而求出当前时刻的估计值。

设随机线性离散系统的方程为:

式中，xk，yk和 uk－1分别为状态量、观测量和输入量;F为状态转移矩阵;G为输入转移矩阵;wk－1为系统过程噪声矩阵;Hk为测量矩阵;vk为测量噪声矩阵。其算法流程如图2所示。

图2 卡尔曼滤波算法流程

3.2 基于主动建模的改进LQG控制

3.2.1联合估计

主动建模是指在对模型中的状态进行估计时采用在线估计的方法，为系统实时地建立相对准确的模型。设含有时变参数的离散系统状态空间方程

如下:

式中，xk为状态量;sk为时变参数。

若在估计式(14)中xk与sk的值时采用了同一种估计算法，则这种估计方法就称为“联合估计”。为了便于估计将式(14)中的xk与sk组合在一起成为增广的状态量，即 x'k=［xk，sk］，那么式(14)可写为如下的形式:

用卡尔曼滤波估计算法对式(15)中的x'k进行估计，从得到的增广状态量估计结果中即可得到时变参数的估计值。

3.2.2控制器重构

将风扰动的估计值反馈给控制器，实现控制器的重构，从而实现有效控制。图3给出了控制器重构的原理示意图。

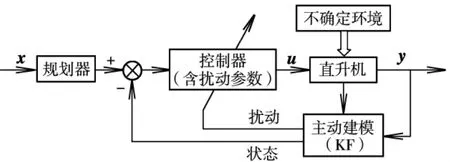
图3 控制器重构原理

4 仿真实验

4.1 纵向仿真

文献［8］中给出了纵向运动方程中参数数值的大小，将其带入式(1)后得到下列矩阵:

通过矩阵A求得纵向运动方程的零极点，如图4所示。

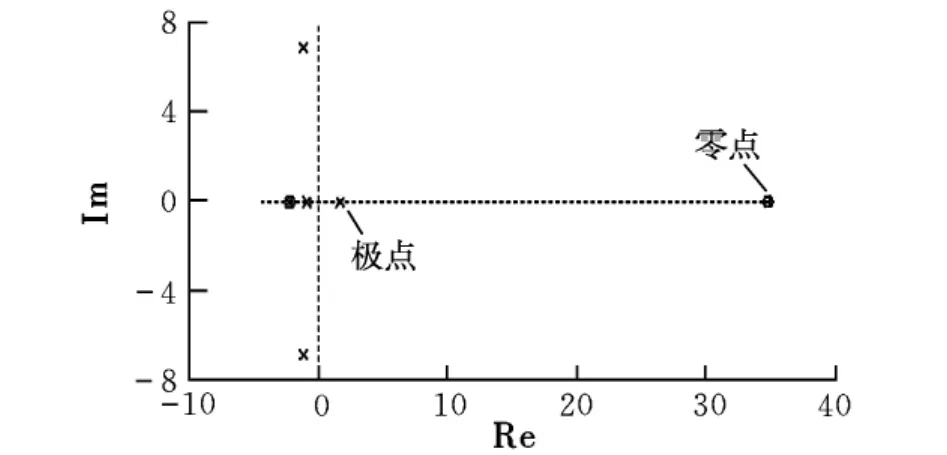
图4 纵向运动方程的零极点图

从图4可以看出，有一个零点和一个极点位于s复平面的右半平面，说明系统是不稳定的。经过多次反复的试验，得到LQR控制器中的q和r的参数取值如下:

当直升机处于大气紊流场中时，紊流的大小和方向是未知的，可由式(10)仿真得到。图5给出了卡尔曼滤波对大气紊流的估计结果。

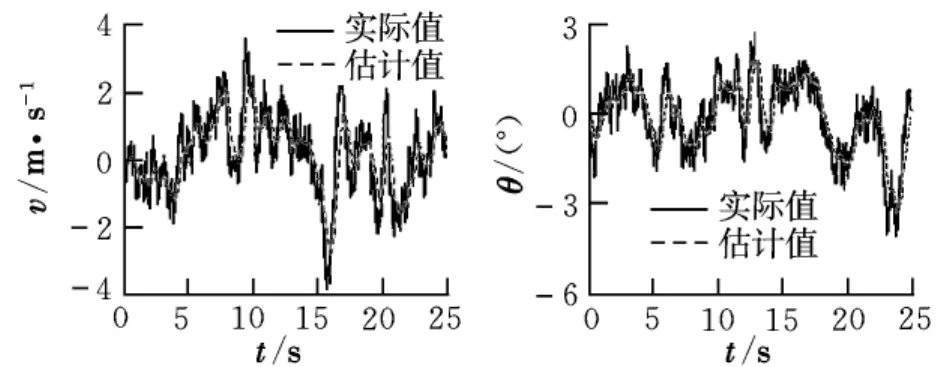
图5 卡尔曼滤波对大气紊流的估计

从图5可以看出，卡尔曼滤波能实时跟踪上大气紊流的变化情况。图6给出了大气紊流对纵向运动的影响。

图6 大气紊流对纵向运动的影响

从图6可以看出，大气紊流使直升机偏离原来的平衡位置，本文提出的控制方法对俯仰角的控制效果良好，且稳态误差在10%之内，而对纵向线速度的控制效果不是很理想。

4.2 横向仿真

文献［8］中给出了横向运动方程中参数数值的大小，将其带入式(2)后得到下列矩阵:

通过矩阵A求得横向运动方程的零极点如图7所示。

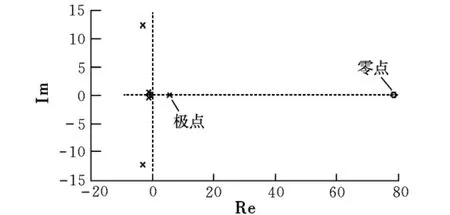
图7 横向运动方程的零极点图

从图7可以看出，有一个零点和一个极点位于s复平面的右半平面，说明系统是不稳定的。经过多次反复的试验，得到LQR控制器中的q和r的参数取值如下:

当直升机处于大气紊流场中时，紊流的大小和方向是未知的，可由式(10)仿真得到。图8给出了卡尔曼滤波对大气紊流的估计结果。

图8 卡尔曼滤波对大气紊流的估计

从图8可以看出，卡尔曼滤波能实时跟踪上大气紊流的变化情况。图9给出了大气紊流对横向运动的影响。

从图9可以看出，大气紊流使直升机偏离原来的平衡位置，本文提出的控制方法对横向线速度的控制效果良好，且稳态误差在5%之内，而对滚转角的控制效果不是很理想。

5 结束语

针对大气紊流环境下无人直升机飞行稳定性问题，提出了一种将主动建模技术与LQG控制相结合的控制算法。通过仿真实验可以看出，该种控制方法中的卡尔曼滤波能够实时跟踪大气紊流的变化情况，并且对大气紊流有一定的抑制作用。该种控制方法的控制效果并不是十分理想，仍需要更深入的研究与思考。

［1］ 阮颖铮，田军.飞行器翼身结合部的散射特性分析［J］.航空学报，1992，20(3):51-55.

［2］ 张文明，代冀阳，吴剑.采用LQR方法的纵列式直升机悬停控制与仿真［J］.微计算机信息(测控自动化)，2010，26(9):172-174.

［3］ 刘冰，艾剑良.基于LQG/LTR方法的飞机自动着陆系统设计［J］.动力学与控制学报，2010，8(1):92-96.

［4］ 姜哲，赵新刚，齐俊桐，等.基于主动建模的无人直升机增强LQR控制［J］.吉林大学学报(信息科学版)，2007，25(5):553-559.

［5］ 肖业伦，金长江.大气扰动中的飞行原理［M］.北京:国防工业出版社，1993.

［6］ 汪沛，张峰，赵振鹏.飞行性能仿真中风场模型的研究［J］.微计算机信息(测控自动化)，2008，24(10):302-304.

［7］ 沈福生.小型无人直升机飞行力学参数化模型辨识研究［D］.南京:南京航空航天大学，2008.

［8］ Dalei Song，Juntong Qi，Lei Dai，et al.Modeling a smallsize unmanned helicopter using optimal estimation in the frequency domain［C］//15th International conference on Mechatronics and Machine Vision in Practice.Auckland，New-Zealand，2008:97-102.

［9］ 王文龙.大气风场模型研究及应用［D］.长沙:国防科学技术大学，2009.