一种CCD工作寿命预计方法

李立，李晓潮

（重庆光电技术研究所，重庆 400060）

一种CCD工作寿命预计方法

李立，李晓潮

（重庆光电技术研究所，重庆 400060）

介绍了一种适用于电荷耦合器件 （CCD）的工作寿命预计方法。对CCD的失效模型进行了分析，并进行加速寿命试验，试验结果与理论分析结果较好地吻合。试验结果表明，对于一款成熟应用的CCD，其工作寿命值与其质量等级有直接的关系；质量等级越高的器件，其工作寿命值也越长。

电荷耦合器件；工作寿命；预计

0 引言

电子产品的寿命预计是在设计阶段，根据设计中所选用的电路程式、元器件、可靠性结构模式、工作环境、工作应力等统计数据，可以推测产品可能达到的寿命水平。

工作寿命预计作为一种设计工具，主要目的在于检查产品研制方案的合理性。预计可从可靠度、性能、重量、费用和研制周期等条件来选择最佳的设计方案，用于了解设计中的薄弱环节，有助于设计人员及时改进。

通过对工作寿命预计，设计人员可以推测产品能否达到规定的可靠性要求，并且寿命预计结果不仅用于指导设计，还可以为转阶段决策提供信息，为可靠性试验制定维修计划、保障性分析、安全性分析和生存性评价等提供信息，帮助提出和确定可靠性实施计划，并为可靠性指标的分配和可靠性保障设计提供依据。

对于电荷耦合器件 （CCD）来说，由于是半导体光电成像器件，相对于其它半导体器件来说，在考虑光电参数的同时，还对成像质量有严格的要求，如漏光、残像等[1]，而CCD的通用规范中只规定了2 000 h的稳态寿命试验[2]。因此，对CCD的工作寿命预计应考虑到器件的特点来制定相应的方法。

1 CCD工作寿命预计理论计算

对CCD的工作寿命预计采用的是GJB/Z 299C-2006《电子设备可靠性预计手册》中的方法[3]，确定其中可以改进的薄弱环节，在设计与制造流程当中不仅要予以特别注意，而且要选择适当的方法进行改进，以提高整个器件的工作寿命。

本文选取一款1 024×1 024全帧转移CCD作为试验对象，根据GJB/Z 299C-2006标准的规定，CCD属于半导体单片集成电路中的存储器类器件，其工作失效率预计模型表示为：

式 （1）中：λp——器件工作失效率，10-6/h；

πQ——质量系数；

πT——温度应力系数；

πV——电压应力系数；

πE——环境系数 ；

πL——成熟系数；

C1及C2——电路复杂度失效率；

C3——封装复杂度失效率。

通过具体的应用环境、设计工艺水平等条件来确定式 （1）中的各个参数。

环境系数πE选定为地面良好GB，故可得πE＝1.0。

在GJB/Z 299C-2006中，规定质量系数πQ与器件的质量等级相关，而质量等级主要分为A、B、C 3级，该器件的质量等级为A4级，则质量系数πQ取0.25。

在GJB/Z 299C-2006中规定的 “成熟系数”πL也分为3个等级，该器件作为稳定生产的产品，因此质量系数πL取1。

温度系数πT取决于器件的工艺和器件工作的结温Tj，对应关系可在标准GJB/Z 299C-2006中查出。器件工作的结温可由式 （2）表示：

式 （2）中：Tc——管壳温度，℃；

Rth（j-c）——结到管壳的热阻，℃/W；

P——器件的工作时的最大功率。

按照GJB/Z 299C-2006的规定，在地面良好条件下TC取35℃，器件的封装形式为PGA，则Rth(j-c)取38，器件工作时的最大功率P为1.5W，可以得到器件工作时的结温Tj＝35+38×1.5=92℃，由GJB/Z 299C-2006标准中表5.2.2-12可得当Tj=92℃时πT取4.83。

由于本器件实际工作时的电源电压为15 V，按GJB/Z 299C-2006中表5.2.2-14及5.2.2-15的规定，电压应力系数πv＝1.81。

本器件的规模为1 024×1 024=1 048 576，按照GJB/Z 299C-2006的规定，电路复杂系数C1＝2.304 0，C2＝0.224 0，封装形式为PGA非气密性封装，引出端数为68，则封装复杂度失效率C3＝0.639 6。

将以上数值带入，最后可以计算出失效率

可得到器件寿命为1/λp=188 870 h。

2 加速寿命试验

寿命试验是寿命预计的一个重要内容，通过这种试验，借助寿命-应力关系模型[4]，可以了解产品的寿命特征、失效规律，计算出产品的失效率和平均寿命等可靠性特征量，以验证理论计算的合理性。

从提高统计分析的准确度来说，最好是做到全部样品失效才结束试验，这就要求产品的数量要足够多，试验时间要足够长，但从产品的研制角度来看一般很难满足这两点要求。但从统计分析的角度来看，只要有一部分试验样品失效就可以停止试验，再采用一定的统计方法就可以计算出其寿命值而不必等到全部样品都失效，这种方法被称为截尾法，现在寿命试验大部分采用的都是截尾法。

截尾法分为定时截尾和定数截尾。定时截尾法是在规定的时间内进行寿命试验，在试验结束后统计失效的器件概率来计算其寿命；而定数截尾则是先规定器件的失效率，在失效率达到规定值后停止试验并计算其寿命。

本文对器件的寿命试验采用的是定时截尾法。定时截尾法的优点是由于预先规定好试验时间，因此能够控制试验的时间进度，适合于时间节点要求比较紧的研制项目。同时为了进一步缩短试验时间，还采用了加速寿命试验的方案，选用的加速应力的温度，具体的试验条件如下：

a）试验器件为8只1 024×1 024全帧转移CCD。

b）寿命试验时器件为正常工作状态，工作频率为10 MHz。

c）温度加速应力为125℃。首先，125℃作为半导体器件的常用存储温度，不会存在因过大应力使器件迅速失效的现象；其次，125℃作为半导体器件性能的一种常用评价温度，也可了解器件在经历长时间该温度水平的应力下的参数水平，对器件的高温工作状态具有一定的指导意义。

d）失效判据。针对该器件的特点，在寿命试验中采取了如下的失效判据：

1）暗信号幅度：≥10 mV/s；

2）饱和电压：≤450mV；

3）水平转移效率：≤0.999 95；

4）图像质量：有行缺陷或列缺陷出现，或新的点缺陷产生。

e）试验时间。从理论上讲，试验时间越长，试验的置信度就越高，所获得的结果就越精确。本次寿命试验的时间约定为4个月。

试验前8只器件的参数如表1所示。

试验结束后器件的参数如表2所示。

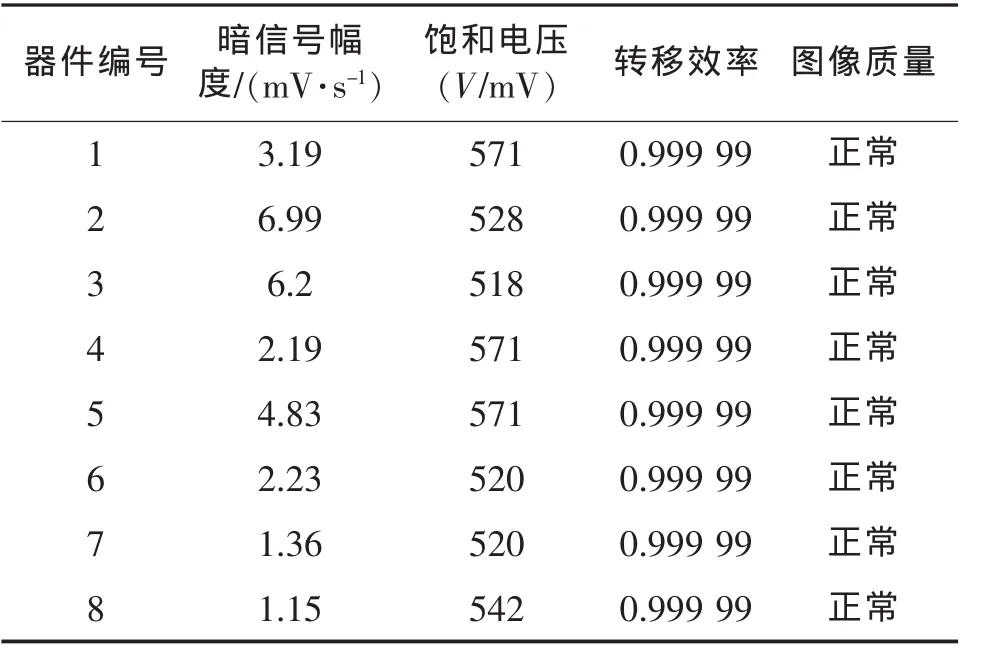
表1 寿命试验前器件参数

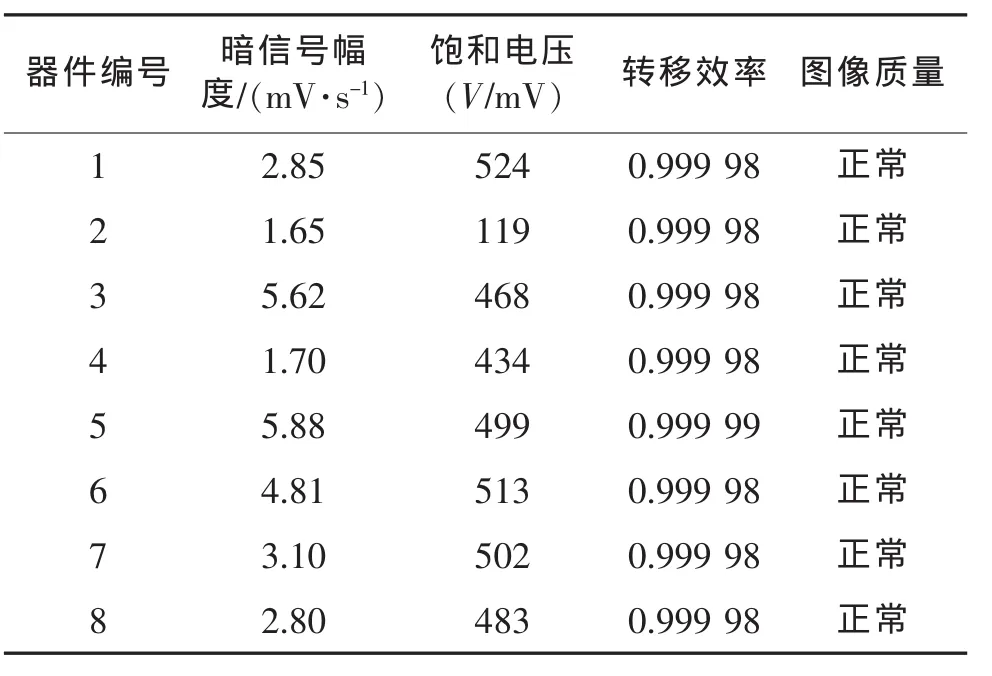
表2 寿命试验后器件参数

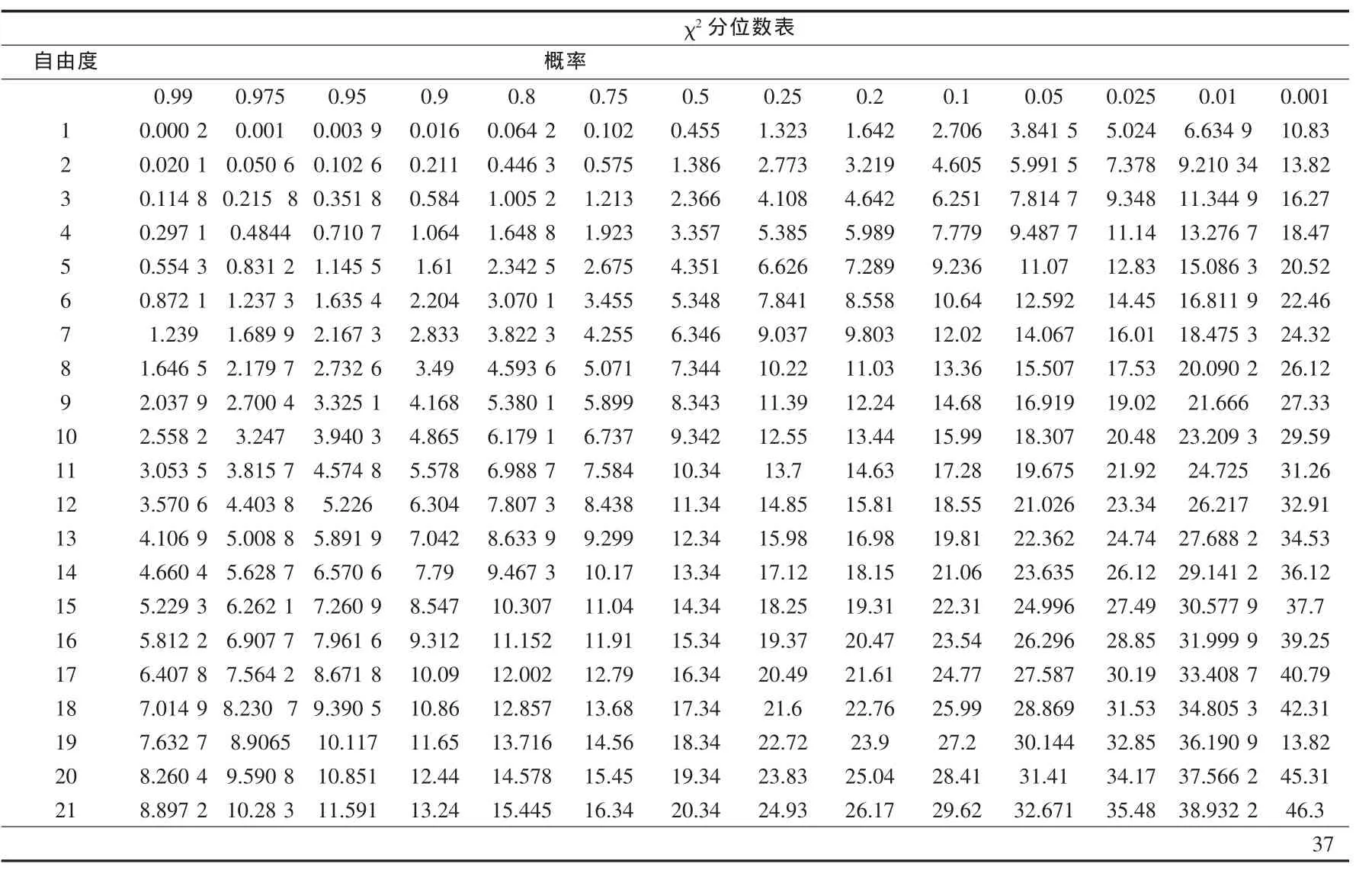
表3 分位数分布表

根据试验前规定的失效判据，编号2和4两只器件的饱和电压低于450mV，故判定8只器件中有两只出现失效。

根据上述试验结果，可以计算出125℃下器件的寿命，如式 （3）所示：

式 （3）中：M——125℃下器件的寿命值；

T——试验时间；

N——试验器件数；

χ2(1-c，2r+2)为分位数分布表，如表3所示；其中c是置信水平，r是失效数。

将试验条件及试验结果带入式 （3）：试验时间T=3 264 h，试验器件N=8只，失效只数r=2只；取置信度c=0.95。

可求得125℃下器件的寿命下限M=4 147 h。

下面再通过计算加速因子来推算器件在常温下的寿命。依据阿伦斯方程：

对于CCD来说，激活能ΔE的选取范围为0.4～1.4 eV，为了求取寿命下限，选取加速因子为0.4 eV。T1为正常工作温度25℃，T2为加速试验时的工作温度125℃，k为波尔兹曼常量，通过计算得出加速因子大小为48。

常温下器件工作时的寿命值=M*加速因子 = 199 056 h。

从试验结果中可以看出，通过CCD寿命模型得到了寿命预计值与实际对器件进行加速试验得到了寿命值能够较好地吻合，说明了该CCD寿命预计模型的合理性以及对CCD的适用性。

3 结束语

通过以上分析及试验可以看出，根据CCD寿命预计模型的原理，CCD的寿命与器件的质量等级、使用环境、电应力环境、结构规模、工作模式以及封装方式的因素有关。通常一个成熟应用的产品，其使用环境、电应力环境、结构规模、工作模式以及封装方式等参数都是固定的。在这种情况下，器件的寿命最主要是受质量等级的影响，质量等级越高，器件的寿命也越长。因此，对于一款成熟应用的CCD来说，若要获得更长的使用寿命，则应选择质量等级更高的器件。

[1]米本和也.CCD/CMOS图像传感器基础与应用 [M].北京：科学出版社，2006.

[2]GJB 5968-2007，电荷耦合成像器件通用规范 [S].

[3]GJB/Z 299C-2006，电子设备可靠性预计手册 [S].

[4]罗雯.电子元器件可靠性试验工程 [M].北京：电子工业出版社，2005.

Prediction of the Operating Life for CCDs

LILi，LIXiao-chao
（Chongqing Optoelectronics Research Institute，Chongqing 400060，China）

In this paper,a prediction method for the operating life of CCDswas introduced.The failure mode of a CCD was analyzed and the accelerated life test was performed.The test results fit well with the theoretic prediction results.It is shown that for a mature CCD，its operating life is directly related to its quality level.The quality level is higher，the operating life is longer.

CCD；operating life；prediction

TN386.5

A

1672-5468（2012）03-0049-05

2011-12-16

2012-06-12

李立 （1981-），男，重庆人，重庆光电技术研究所工程师，硕士，从事CCD的设计及可靠性研究工作。