半平面Poisson方程边值问题分析
2012-02-28郭时光
郭时光
(四川理工学院理学院,四川 自贡643000)
其中:G(M,M 0)是区域V的Green函数;n M0是边界∂V上点M 0(x 0,y 0,z0)处关于区域V的向外法线方向。
0 前 言
设有上半平面Poisson方程边值问题[1-6]

其中:f与g均为连续且可积的函数。
对于问题 (1),在目前众多的数学物理方程著作中,有的未能给出其解[1,2],有的直接采用Poisson方程Direchlet问题的Poisson公式,从而得出其解的积分表达式[3,4]为

其中G(x,y;x0,y0)是上半平面0≤y的Green函数

然而,一方面,问题 (1)不是严格的Direchlet问题,因为上半平面的边界可视为由四条直线

组成的,该问题的边界条件是不完整的。因此,从逻辑上来说,这个问题用Poisson方程Direchlet问题的Poisson公式来定解是说不通的;另一方面,在式 (2)中,如果代入y=0,或者令y→0,则均得u(x,0)=0。可见,这个解不能满足问题 (1)中的边界条件,因而人们难以接受这个解。那么,这个问题到底应该如何来解呢?鉴于这个问题的重要性,下面讨论这个问题。
1 引 理

引理[5,6]在Poisson方程 Direchlet问题中,设定解区域V具有逐片光滑的边界∂V,自由项f(M)与g(M)均为连续可积函数。如果V是二维区域,则问题 (4)存在解的积分表达式

其中:G(M,M0)是区域V的Green函数;nM0是边界∂V上点M0(x0,y0,z0)处关于区域V的向外法线方向。
2 问题的解
考虑如式 (3)所示的Green函数G=G(x,y;x0,y0)。计算它关于边界直线y=0的向外法线方向导数,因为上半平面关于边界直线y=0的向外法线方向为n=(0,-1),故得

分别计算Green函数G关于上半平面其它三个边界直线的向外法线方向导数,得

所以,如果用∂V表示上半平面的四条边界直线,则无论将目标函数u在其中三条边界直线y=+∞,x=±∞上赋予任何连续的值,总有
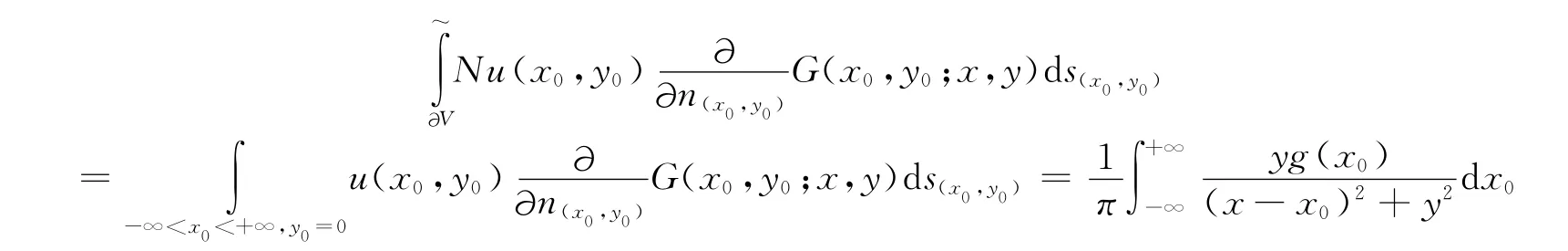
这样,将问题 (1)视补足边界条件而成为Direchlet问题之后,则可用引理的二维Poisson方程Direchlet问题Poisson公式计算。将上式中参变点坐标(x0,y0)与变点坐标(x,y)互换,然后代入公式 (5),最后将积分化为重积分,于是得到解的积分表达式 (2)。
为了改变式(2)不满足边界条件这一状况,如果y>0,将式(2)中的前面一个积分作变换x0=x+ys,则得
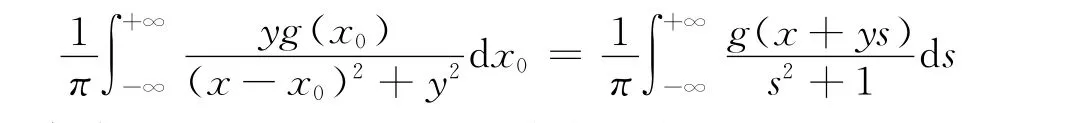
如果y=0,也用上式右边代替左边,这样,解的积分表达式 (2)变为

3 解的正规性
证 根据条件,可以将y=0代入式 (6)中,用G(x,0;x0,y0)=0,得

当y>0时,式 (6)可以表示为式 (2)。将式 (2)作关于自变数x,y的Laplace运算△,则用条件,等式 △G(x,y;x0,y0)=-δ(x-x0,y-y0),以及δ函数的筛选性质,得

由此可见,这时表达式 (6)是问题 (1)的正规解。
[1] 查中伟.数学物理偏微分方程 [M].成都:西南交通大学出版社,2005:139-140.
[2] 郭玉翠.数学物理方法 [M].北京:北京邮电大学出版社,2003:313.
[3] 王元明.数学物理方程与特殊函数 (第三版)[M].北京:高等教育出版社,2003:95-97.
[4] 郭时光.数学物理方程 [M].成都:西南交通大学出版社,2005:112.
[5] 谷超豪,李大潜.数学物理方程 [M].北京:人民教育出版社,1979:115.
[6] 严正军.数学物理方程 [M].合肥:中国科学技术大学出版社,1996:34.
