单轴荷载下饱水岩石静态和动态抗压强度的细观力学分析*

王 斌，李夕兵

(1.湖南科技大学能源与安全工程学院，湖南 湘潭411201;2.中南大学资源与安全工程学院，湖南 长沙410083;3.煤矿安全开采技术湖南省重点实验室，湖南 湘潭411201)

自然界中的岩石是一种存在着大量微观裂隙等缺陷的非均质不连续体，由于这些裂隙的存在，在水压力的作用下，水会渗透到岩石裂隙中成为孔隙自由水，水成为影响岩石力学性质的重要因素。在跨流域调水、修建水库和海峡隧道、受地下水影响的地下采矿等工程中岩石常处于水饱和状态，工程岩体在水渗流与应力相互作用下的变形、损伤破坏及稳定性是许多工程学科共同关心的课题［1］。关于饱水岩石力学性质的影响越来越被重视。A.B.Hawkins 等［2］对35 种砂岩的单轴抗压实验表明，饱水强度是干燥强度的0.759 倍，受水岩化学作用和孔隙水压力等的影响，岩石遇水静态强度降低已成为工程地质学界不争的事实［3-5］。许多重大工程均面临岩石动力学特性与动力稳定性问题，如地震、滑坡等地质灾害的发生都涉及到岩石类脆性材料的动态力学特性问题［6］，饱水岩石动态强度研究日益受到关注。研究表明，岩石处于水饱和条件下的动态强度特性比静态条件有所改善。A.M.Rubin 等［7］和楼沩涛［8］的分离式霍布金森压杆实验研究表明，饱水花岗岩比干燥时更难拉断。葛洪魁等［9］结合声波技术测得饱和砂岩静态与动态杨氏模量比值约0.6，从侧面反映出饱水砂岩动态强度大于静态强度。王斌等［10］采用改进的SHPB 实验装置对饱水砂岩进行实验，结果表明动态加载条件下饱水动态抗压强度与风干动态强度相近，这与静载条件下饱水砂岩强度降低的结果相反。可见，岩石处于水饱和条件下动态与静态强度特性存在差异，但这种差异从传统的宏观力学实验和理论分析方面是难以解释的。

细观力学方法以断裂力学理论为基础，能描述微裂纹的成核、扩展和汇合，并据此反映材料宏观力学性能的变化，适合研究含固有裂纹的岩石材料，因此采用细观力学方法来分析岩石破裂演化过程及破坏规律的研究成果较多。但对于饱水岩石，现有的研究微裂纹的模型较多是从静态加载条件出发［4-5，11］，而动态加载条件的岩石断裂研究的却主要是不含水的干燥岩石［12-13］，因此从岩石细观结构将饱水岩石动态强度特性与静态强度特性进行对比分析具有理论和现实意义。

1 岩石全应力应变曲线的细观机制分析

岩石材料的宏观力学特性是材料内部细观力学特性的综合反映。宏观上根据岩石室内压缩实验获得应力应变曲线来研究岩石单轴抗压强度是常用的方法，并通过曲线的斜率变化从岩石细观角度进行解释。根据文献［14-15］，随着外载荷的逐渐增大，与微裂纹扩展情况相对应的4 个宏观特征应力为:闭合应力σcs、起裂应力σci、破损应力σcd、峰值应力σc(单轴抗压强度)，如图1 所示。对于单轴荷载条件，该曲线通常分为为5 个阶段:

(1)加载初期，当σ ＜σcs时，微裂纹压密阶段(OA 段)。岩石试件刚度逐渐增大，岩石原生裂纹形状会发生变化，甚至会完全完闭合。

(2)当σcs≤σ＜σci时，线弹性变形阶段(AB 段)。岩石材料表现为理想弹性体。

(3)当σci≤σ＜σcd时，微裂纹稳定扩展(BC 段)。部分裂纹发生摩擦滑动和自相似扩展，出现翼形裂纹。

(4)当σcd≤σ＜σc时，微裂纹不稳定扩展(CD 段)。翼形裂纹的扩展方向趋向于外力加载方向，逐渐扩展到临界长度，相邻微裂纹将迅速串接为连续裂纹。

(5)当σ≥σc时，微裂纹失稳扩展(DE 段)。出现宏观裂缝带，岩石发生破坏，干燥岩石易出现劈裂破坏模式，含水岩石破坏模式较复杂，表现为拉剪或压剪破坏模式［11］。因贯通裂缝的结构效应，破裂的岩石具有残余强度。

动态加载条件不会改变岩石破裂的这种基本模式，同时饱水岩石和干燥岩石破坏都可归结为内部裂纹的起裂、扩展和连通［6，11］。

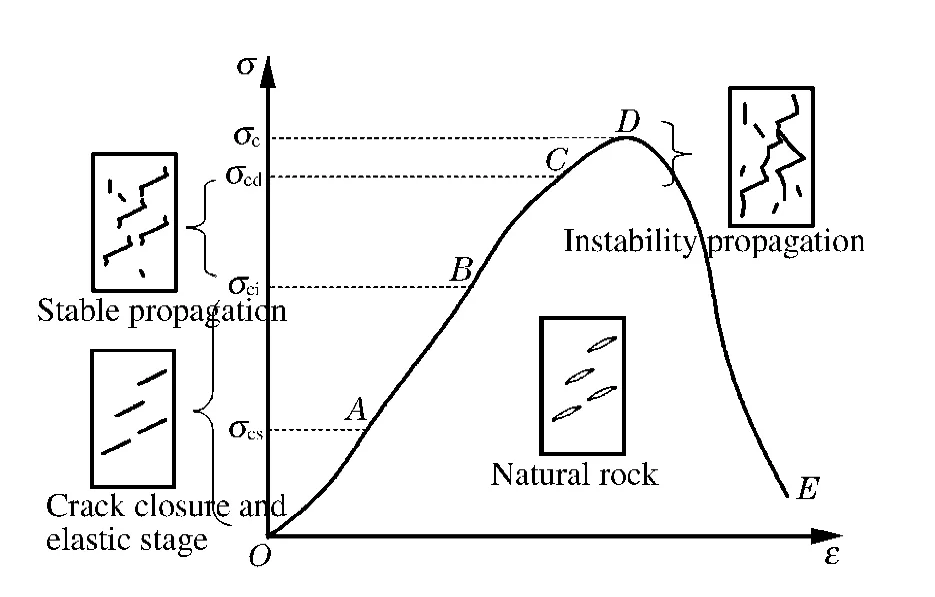
图1 岩石全应力应变曲线的细观机制分析Fig.1 Meso-mechanism of rock stress and strain curve

2 岩石裂纹静、动态断裂准则

2.1 静态载荷和动态载荷的区分

对于岩石静、动力学的区分至今尚无统一和严格的规定，一般根据应变率作为区分静态与动态的指标。当＜10－5s－1时，为蠕变荷载，介于10－5～10－1s－1时，为静态荷载，介于10－1～101s－1时，为准动态荷载，介于10 ～103s－1时，为动态荷载，＞104s－1时，为超动态荷载［6］。静态荷载可以通过普通液压伺服试验机实现，动态荷载一般采用霍普金森压杆实现，超动态荷载可由轻气炮或平面波发生器加载等获得。

2.2 裂纹静态和动态断裂准则及关系

岩石裂纹断裂准则中常用的基本参量是应力强度因子和断裂韧度，这2 个量控制着静态或动态断裂过程的发生和发展，在外载荷作用下，当岩石内部固有裂纹应力强度因子达到材料的断裂韧度时，固有裂纹开始扩展，直到岩石材料宏观上发生破坏。

岩石类材料一般简化为Ⅰ型断裂问题，不考虑亚临界状态，在静载荷作用下的裂纹扩展准则为

式中:Ks表示裂纹的静态应力强度因子，KC，s表示材料的静态断裂韧度。

在动载荷作用下，常用的裂纹扩展准则

式中:Kd表示裂纹的动态应力强度因子，KC，d表示材料的动态断裂韧度。

动态断裂问题相对复杂，动态应力强度因子的大小不仅与裂纹尺寸和远场应力有关，还是时间的函数，涉及复杂的非线性运动边界问题，处理上非常复杂，目前尚无统一的数学理论［16］。一种常用的近似方法是将动态应力强度因子表示为静态应力强度因子的函数［17］

式中:K(t)表示裂纹扩展速度为v 时的动态应力强度因子，K(0)是K 的静态值，k(v)是一个普适的、与裂纹几何形状无关的速度影响因数

式中:cR为介质的瑞利波波速，cP为介质的纵波波速。

裂纹动态扩展与静态扩展的区别，从能量的角度说，是由动载引起的惯性力产生动能，进而导致裂纹按速度v 作动态扩展。当v=0 时，k(v)=1;当裂纹的扩展速率达到极限速率即材料的瑞利波波速cR时，k(v)=0。

通常，k(v)常用以cR相关的近似表达式［18］，考虑到介质纵波波速cP在岩石研究中应用更广泛，采用与cP相关的k(v)近似计算更方便。纵波波速cP和瑞利波波速cR与介质的弹性性质存在如下关系［19］

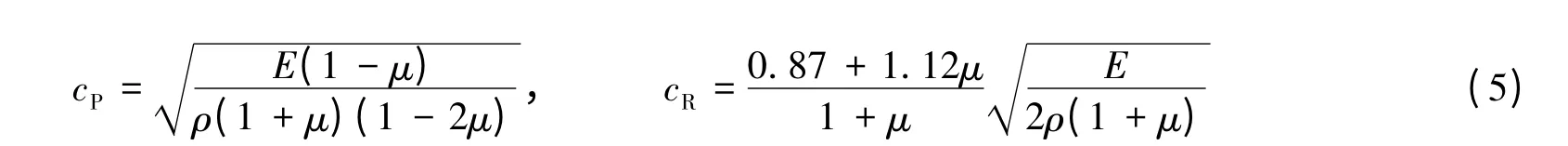
式中:E 为弹性模量，ρ 为材料介质密度，μ 为泊松比。

则可得

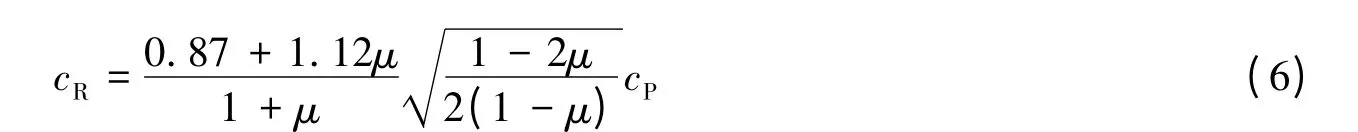
根据式(6)可得cR/cP随泊松比变化的关系曲线，如图2 所示。

当μ=0.25 时，cR=0.531cP，代入式(4)可得

根据式(7)可得k(v)随裂纹扩展速度的变化，如图3 所示。实测砂岩纵波速度cP=4.5 km/s。

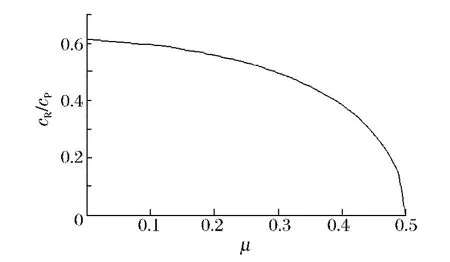
图2 cR/cP 与泊松比的关系曲线Fig.2 Relationship curve of cR/cP and poisson ratio

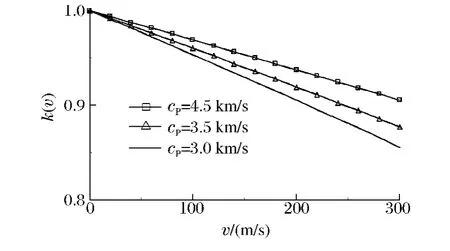
图3 k(v)与裂纹扩展速度的关系曲线Fig.3 Relationship curves of k(v)and crack expansion speed

2.3 裂纹扩展的翼形滑动模型

翼形裂纹扩展和串接是削弱岩石试件承载强度的根本原因［12］，因此采用图4 所示的岩石断裂常用的滑动模型来分析饱水岩石动态和静态强度的差异。该模型假设裂纹面的摩擦力和正压力满足莫尔-库仑定理，当外载在裂纹面上引起的剪应力超过摩擦力时，裂纹面将滑动从而引起裂尖应力集中，并最终导致张开型翼形裂纹的萌生和扩展。H.Horii 等［20］、P.S.Steif［21］、王元汉等［22］和李银平等［23］进行了相关研究。根据文献［23］，假设翼裂纹长度l 适中，引入文献［20］中提出的翼形裂纹应力强度因子计算公式

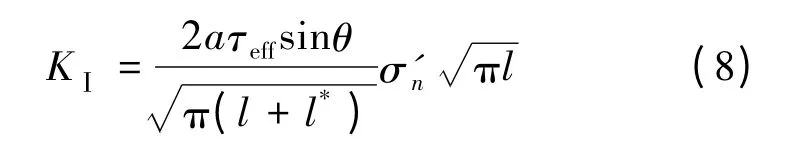
式中:2a 为初始裂纹长度;l*为当量裂纹长度，l*=0.27a;τeff和σ′n分别为主裂纹面上的剪应力和翼裂纹面上的法向应力(假定压应力为正)。

无水单轴静载条件时，有

式中:fs为静态无水条件下裂纹面摩擦因数。

为便于分析饱水状态的岩石，根据文献［24］，不考虑微裂纹之间的相互作用，认为当图4 所示的翼裂纹长度l 达到临界长度lc时，岩石裂纹发生串接，试件发生断裂，此时所需的外载即岩石试件的抗压峰值应力。

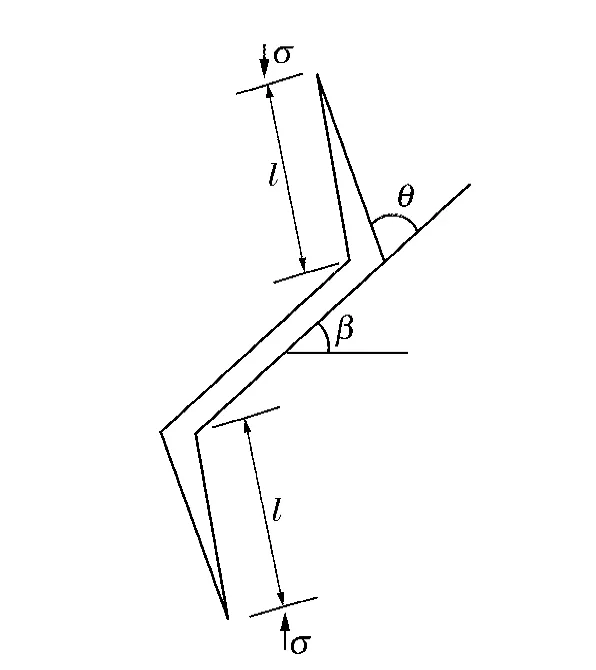
图4 滑动裂纹模型Fig.4 Sliding crack model

3 饱水岩石静、动态裂纹扩展分析

3.1 受静、动态载荷的饱水初始裂纹

为了分析饱水岩石中孔隙自由水对静、动状态下裂纹扩展的影响，须从饱水初始裂纹开始分析。饱水岩石内初始裂纹分布一般是随机的，也呈三维分布，同时饱水岩石需考虑裂纹中充满自由水，为研究方便，对于任意含水的初始裂纹设为平面穿透，其长度为2a，角度为β，分别受静载σs和动载σd作用，如图5 所示。

3.2 静态条件下水促进裂纹扩展

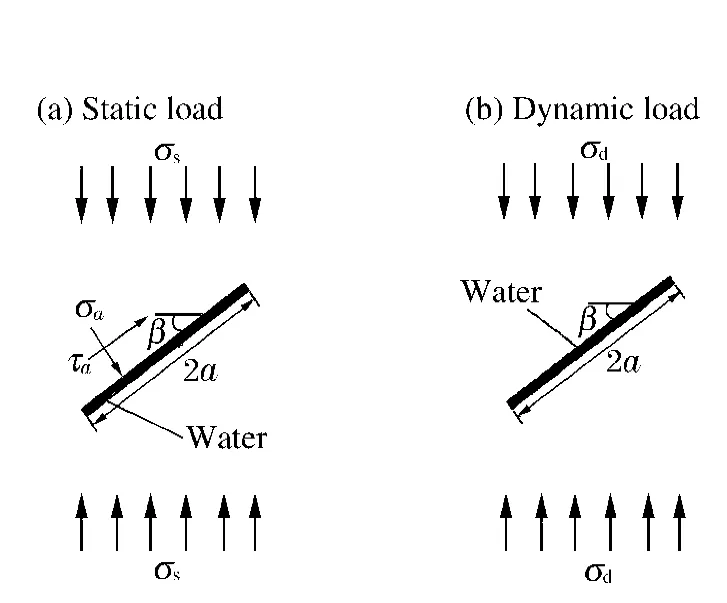
图5 单轴载荷下含水初始裂纹Fig.5 Initial crack fracture with water under uniaxial load

由图1，在静态加载条件下的体积压缩阶段，岩石初始裂纹受压闭合，使自由水产生孔隙水压力，H.Oshita 等［25］研究表明，孔隙水压力逐渐增长并与外载荷呈线性关系。随着静载荷的增大，翼裂纹产生，翼裂纹扩展的速度相对于实验加载的速度要快得多［26］，这样自由水有足够的时间向翼裂纹尖端扩散，产生类似“楔入”的作用，此时翼裂纹有向外挤压的应力psw，如图6 所示。同时自由水在翼裂纹尖端具有类似“虹吸”的效应而能充满翼裂纹的尖端，并在一定程度上可润滑裂纹接触面，从而促进岩石中脆性微破裂活动，促进了裂纹扩展。

因此，不考虑水对裂纹面的化学损伤，静载条件下，含孔隙自由水的初始主裂纹面上的剪应力τsw和翼裂纹面法向应力σsw(假定压应力为正)分别为

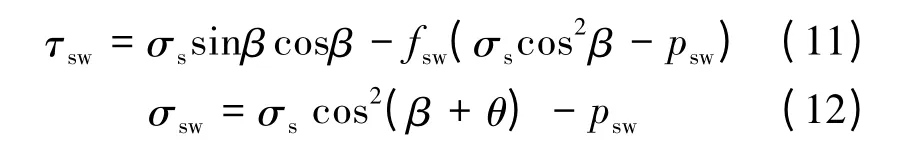
式中:fsw为静态含水条件下裂纹面摩擦因数。

3.3 动态条件下水抑制裂纹扩展

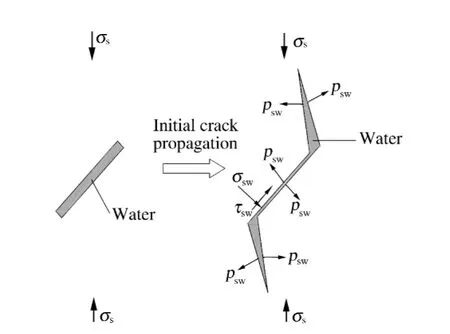
图6 静载条件下自由水对裂纹表面的作用力Fig.6 Pressure of crack surface caused by free water under static load

岩石冲击破坏理论与相关实验表明，在动态加载条件下，裂纹动态扩展的速度比静态扩展速度快。动态条件下，裂纹扩展速度远低于实验加载速度，在高应变率时甚至可以视为不排水［6，26］。同时，超动态条件下水是不可压缩的，岩石中的自由水无法在瞬间扩散到整个张开的翼裂纹尖端中，如图7 所示。

在动载条件下，未充满水的翼裂纹会受自由水的表面张力，在裂纹面形成阻碍裂纹扩展的粘结力。饱和混凝土自由水表面张力形成的粘结力［27］

式中:V 为液体的体积，γ 为表面能，ψ 为湿润角，δ为水的弯月面的半径。

ZHENG Dan 等［27］、P.Rossi 等［28］研究了湿混凝土动态断裂强度的影响，在动态加载条件下湿混凝土强度提高的原因是Stefan 效应产生的阻力F′可阻碍裂纹扩展断裂

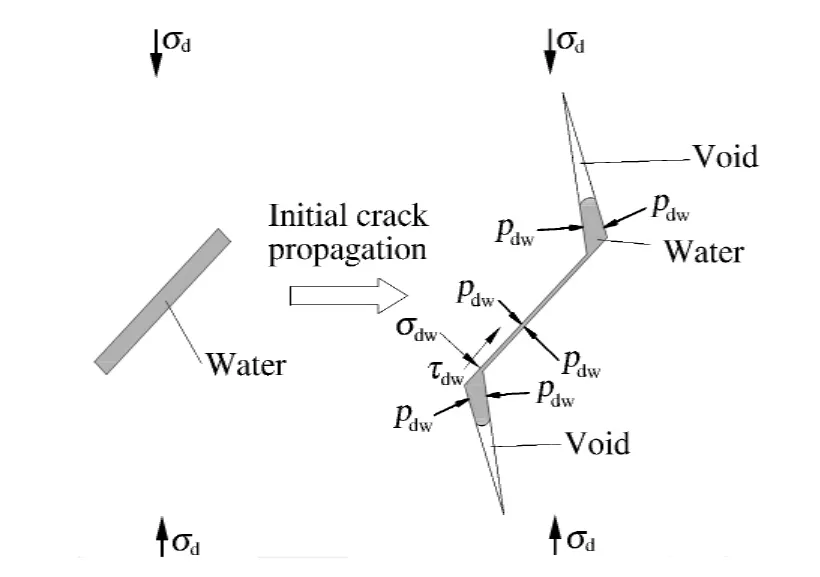
图7 动载条件下自由水对裂纹表面的作用力Fig.7 Pressure of crack surface caused by free water under dynamic load

式中:η 为液体黏度，r 为中间充满有不可压缩黏性液体的两平行圆形平板的半径，为两圆形平板分离的相对速度，h 为两圆形平板的间距。

由式(13)～(14)可以粗略确定图7 中阻碍裂纹断裂破坏的应力

式中:A 为裂纹含水面积。

同样不考虑水对裂纹面化学损伤，动载条件下，含孔隙自由水的初始主裂纹面上的剪应力τdw和翼裂纹面法向应力σdw(假定压应力为正)分别为

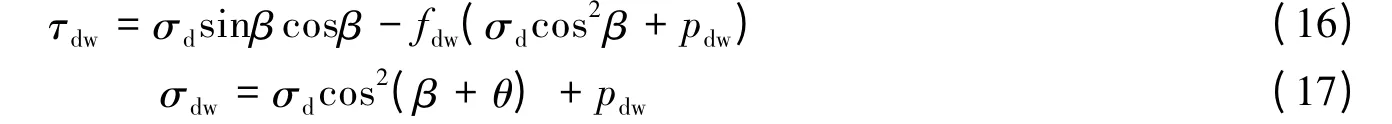
式中:fdw为动态含水条件下裂纹面摩擦因数。

4 基于细观力学的饱水静、动态抗压强度

如前所述，当翼裂纹长度l=lc时，试件发生破坏，当l 较长时，根据文献［23］，可以忽略l*对应力强度因子的影响，这一简化能满足工程应用的需要。因孔隙水在不同加载速率下产生的作用力不同，可以得到无水静载条件、饱水静载条件和饱水动态条件3 种状态下的应力强度因子，根据断裂韧度可确定相应状态下岩石试件的抗压峰值应力。

无水静载条件时，将式(9)～(10)代入式(8)，可得峰值应力

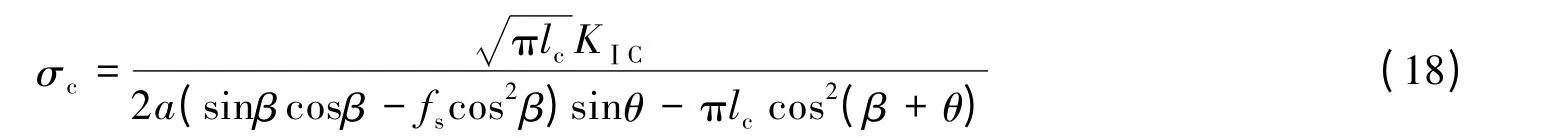
式中:KⅠC为岩石无水静态Ⅰ型断裂韧度。

饱水静载条件时，将式(11)～(12)代入式(8)，可得饱水静态抗压强度

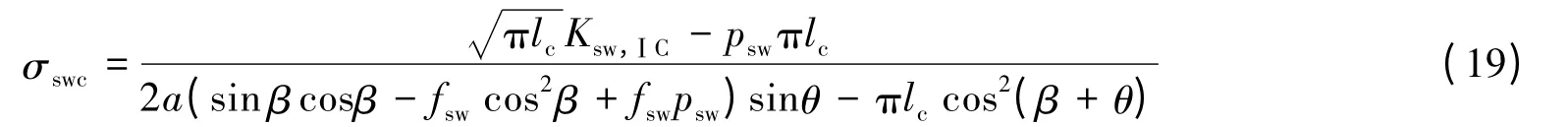
式中:Ksw，ⅠC为岩石饱水静态Ⅰ型断裂韧度。

饱水动载条件时，需引入k(v)，将式(16)～(17)代入式(8)，可得饱水动态抗压强度

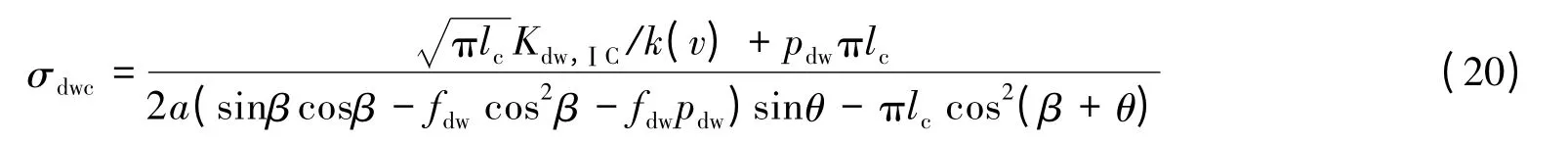
式中:Kdw，ⅠC为岩石饱水动态Ⅰ型断裂韧度。

为定量比较3 种状态下的单轴抗压强度，根据文献［12，29］确定，花岗岩初始裂纹长度为0.75 mm，翼裂纹临界长度lc=1.4 mm，裂纹面的摩擦因数f=0.3，初始裂纹倾角β=45°，翼形裂纹的扩展方向与试件轴向平行，因此θ=45°，泊松比μ=0.25，裂纹扩展速度v=100 m/s，纵波速度cP=4.8 km/s，静态孔隙水压力psw=0.2 MPa，动态孔隙水作用力pdw=0.05 MPa，按式(7)计算可得k(v)=0.971。于是，根据本文计算模型可以得到图8 所示3 种状态下的花岗岩单轴抗压强度随Ⅰ型断裂韧度的变化规律。由图8 可以看出，单轴抗压强度与Ⅰ型断裂韧度成线性比例关系，这与文献［30］的结果一致。在相同断裂韧度下，饱水岩石静态抗压强度＜风干岩石静态抗压强度＜饱水岩石动态抗压强度。

精确地确定动态条件下孔隙水的作用力和裂纹扩展速度是很困难的，由图9 饱水花岗岩动态单轴抗压强度随影响因数k(v)的变化规律可以看出，动态条件孔隙水作用力越大，饱水岩石的动态抗压强度越大;结合图3 曲线，k(v)越小，裂纹扩展越快，饱水岩石的动态抗压强度越大。与之相反，静态条件孔隙水作用力越大，饱水岩石的静态抗压强度越小。

图8 花岗岩单轴抗压强度与Ⅰ型断裂韧度关系Fig.8 Relationship between mode-Ⅰfracture toughness and granite compression strength under uniaxial load

图9 花岗岩动态单轴抗压强度与k(v)的关系曲线Fig.9 Relationship curves of k(v)and granite dynamic compression strength under uniaxial load

5 饱水砂岩静、动态实验结果对比

为验证前述饱水岩石静动态断裂模型的分析结果，采用自然风干和饱水砂岩试件进行实验研究。静态单轴压缩实验在200 t 量程的INSTRON 1346 型电液伺服控制材料试验机上进行，加载应变率为10－5s－1;动态单轴压缩实验在改进研制的SHPB 实 验 装 置 上 进 行［31］，加 载 应 变 率为52 s－1左右。

饱水砂岩试样按《水利水电工程岩石试验规程》(SL264-2001)中自由吸水法，在水中浸泡30 d 后制得。经过实验，相应自然风干和饱水砂岩静动态实验的典型应力应变曲线如图10 所示。由图10 可以看出，砂岩裂隙中存在自由水，会直接影响着饱水砂岩静、动态强度，与自然风干的岩石相比，饱和砂岩在单轴静态压缩条件下强度有所降低，而单轴动态压缩条件下强度有所增加，这与理论模型的结果相符。

图10 自然风干与饱水砂岩的静态及动态应力应变曲线Fig.10 Static and dynamic stress and strain curves of air-dried and water-saturated sandstone

6 结 论

(1)在分析岩石受压全应力应变曲线的细观机制的基础上，从细观微结构角度，探讨了岩石孔隙自由水对裂纹扩展的影响。在静态单轴压缩条件下，初始裂隙受压使自由水产生孔隙水压力，自由水对翼裂纹有向外挤压的应力，促进裂纹扩展，饱水岩石强度降低。在动态单轴压缩条件下，自由水会产生阻碍翼裂纹扩展的粘结力，抑制裂纹扩展，饱水岩石强度增强。

(2)根据翼形裂纹滑动模型，得到饱水单轴条件下动态抗压强度、静态抗压强度的计算公式。该公式表明饱水岩石单轴抗压强度与Ⅰ型断裂韧度成线性比例关系，在相同断裂韧度下，饱水岩石静态抗压强度＜风干岩石静态抗压强度＜饱水岩石动态抗压强度。

(3)本文中未考虑水化学损伤对饱水岩石强度的影响，水化学损伤会导致岩石的微观成分改变和原有微观结构破坏，从而降低饱水岩石动态强度。在对饱水砂岩进行动态单轴压缩实验时，有比风干强度降低的试样。

［1］ 张有天.岩石水力学与工程［M］.北京:中国水利水电出版社，2005.

［2］ Hawkins A B，McConnell B J.Sensitivity of sandstone strength and deformability to changes in moisture content［J］.Quarterly Journal of Engineering Geology＆Hydrogeology，1992，25(2):115-130.

［3］ Vasarhlyi B，Van P.Influence of water content on the strength of rock［J］.Engineering Geology，2006，84(1/2):70-74.

［4］ 汤连生，张鹏程，王洋.水作用下岩体断裂强度探讨［J］.岩石力学与工程学报，2004，23(19):3337-3341.TANG Lian-sheng，ZHANG Peng-cheng，WANG Yang.On fractures strength of rocks with cracks under water action［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23(19):3337-3341.

［5］ 朱珍德，胡定.裂隙水压力对岩体强度的影响［J］.岩土力学，2000，21(1):64-67.ZHU Zhen-de，HU Ding.The effect of intestitial water pressure on rock mass strength［J］.Rock and Soil Mechanics，2000，21(1):64-67.

［6］ 李夕兵，古德生.岩石冲击动力学［M］.长沙:中南工业大学出版社，1994.

［7］ Rubin A M，Ahrens T J.Dynamic tensile-failure-induced velocity deficits in rock［J］.Geophysical Research Letters，1991，18(2):219-222.

［8］ 楼沩涛.干燥和水饱和花岗岩的动态断裂特性［J］.爆炸与冲击，1994，14(3):249-254.LOU Wei-tao.Dynamic fracture behaviour of dry and waterlogged granite［J］.Explosion and Shock Waves，1994，14(3):249-254.

［9］ 葛洪魁，陈颙，林英松.岩石动态与静态弹性参数差别的微观机理［J］.石油大学学报(自然科学版)，2001，25(4):34-36.GE Hong-kui，CHEN Yong，LIN Ying-song.Microscopic mechanism of difference between static and dynamic elastic parameters of rock［J］.Journal of the University of Petroleum，2001，25(4):34-36.

［10］ 王斌，李夕兵，尹土兵，等.饱水砂岩动态强度的SHPB 试验研究［J］.岩石力学与工程学报，2010，29(5):1003-1009.WANG Bin，LI Xi-bing，YIN Tu-bing，et al.Split Hopkinson pressure bar(SHPB)experiment on dynamic strength of water-saturated sandstone［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(5):1003-1009.

［11］ 李宗利，张宏朝，任青文，等.岩石裂纹水力劈裂分析与临界水压计算［J］.岩土力学，2005，26(8):1216-1220.LI Zong-li，ZHANG Hong-chao，REN Qing-wen，et al.Analysis of hydraulic fracturing and calculation of critical internal water pressure of rock fracture［J］.Rock and Soil Mechanics，2005，26(8):1216-1220.

［12］ 李海波，赵坚，李廷芥.滑移型裂纹模型在研究岩石动态单轴抗压强度中的应用［J］.岩石力学与工程学报，2001，20(3):315-319.LI Hai-bo，ZHAO Jian，LI Ting-jie.Study of dynamic uniaxial compressive strength of rock material using sliding crack model［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20(3):315-319.

［13］ Li H B，Zhao J，Li T J.Micromechanical modelling of the mechanical properties of a granite under dynamic uniaxial compressive loads［J］.International Journal of Rock Mechanics and Mining Sciences，2000，37(6):923-935.

［14］ Cai M，Kaiser P K，Tasaka Y，et al.Generalized crack initiation and crack damage stress thresholds of brittle rock masses near underground excavations［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41(5):833-847.

［15］ 刘泉声，胡云华，刘滨.基于试验的花岗岩渐进破坏本构模型研究［J］.岩土力学，2009，30(2):289-296.LIU Quan-sheng，HU Yun-hua，LIU Bin.Progressive damage constitutive models of granite based on experimental results［J］.Rock and Soil Mechanics，2009，30(2):289-296.

［16］ 范天佑.断裂动力学原理及应用［M］.北京:北京理工大学出版社，2006.

［17］ Xie H P，Sanderson D J.Fractal effect of rapidly propagation cracks［C］∥Proceedings of the 2nd International Conference on Nonlinear Mechanics.Beijing，1995:341-344.

［18］ Freund L B.Dynamic fracture mechanics［M］.Cambridge:Cambridge University Press，1990.

［19］ 杨成林.瑞利波勘探［M］.北京:地质出版社，1993.

［20］ Horii H，Nemat-Nasser S.Brittle failure in compression:Splitting，faulting and brittle-ductile transition［J］.Philosophical Transactions of the Royal Society of London，1986，319(1549):337-374.

［21］ Steif P S.Crack extension under compressive loading［J］.Engineering Fracture Mechanics，1984，20(3):463-473.

［22］ 王元汉，徐钺，谭国焕，等.改进的翼形裂纹分析计算模型［J］.岩土工程学报，2000，22(5):612-615.WANG Yuna-han，XU Yue，TAN Guo-huan，et al.An improved calculative model for wing crack［J］.Chinese Journal of Geotechnical Engineering，2000，22(5):612-615.

［23］ 李银平，伍佑伦，杨春和.岩石类材料滑动裂纹模型［J］.岩石力学与工程学报，2007，26(2):278-284.LI Yin-ping，WU You-lun，YANG Chun-he.Comparison of sliding crack models for rock-like materials［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(2):278-284.

［24］ 王海龙，李庆斌.湿态混凝土抗压强度与本构关系的细观力学分析［J］.岩石力学与工程学报，2006，25(8):1531-1536.WANG Hai-long，LI Qing-bin.Mesomechanics analysis of compressive strength and constitutive equation of wet concrete［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25(8):1531-1536.

［25］ Oshita H，Tanabe T.Water migration phenomenon in concrete in prepeak region［J］.Journal of Engineering Mechanics，2000，126(6):565-572.

［26］ 田象燕，高尔根，白石羽.饱和岩石的应变率效应和各向异性的机理探讨［J］.岩石力学与工程学报，2003，22(11):1789-1792.TIAN Xiang-yan，GAO Er-gen，BAI Shi-yu.Discussion about mechanism of strain-rate effect and anisotropy of saturated rocks［J］.Chinese Journal of Rock Mechanics and Engineering，2003，22(11):1789-1792.

［27］ ZHENG Dan，LI Qing-bin.An explanation for rate effect of concrete strength based on fracture toughness including free water viscosity［J］.Engineering Fracture Mechanics，2004，71:2319-2327.

［28］ Rossi P，Van Mier J G M，Boulay C，et al.The dynamic behavior of concrete:Influence of free water［J］.Materials and Structures，1992，25(9):509-514.

［29］ 张志呈.岩体爆破裂纹扩展速度实验研究［J］.爆破器材，2000，29(3):1-7.ZHANG Zhi-chen.An experimental study of crack expansion speed in rock blasting［J］.Explosive Materials，2000，29(3):1-7.

［30］ 李江腾，古德生，曹平，等.岩石断裂韧度与抗压强度的相关规律［J］.中南大学学报(自然科学版)，2009，40(6):1695-1699.LI Jiang-teng，GU De-sheng，CAO Ping，et al.Interrelated law between mode-Ⅰfracture toughness and compression strength of rock［J］.Journal of Central South University(Science and Technology)，2009，40(6):1695-1699.

［31］ Li X B，Zhou Z L，Lok T S，et al.Innovative testing technique of rock subjected to coupled static and dynamic loads［J］.International Journal of Rock Mechanics and Mining Sciences，2008，45(5):739-748.