一种基于逆系统方法的末制导律

范玉洁，周长征

(1.中国空空导弹研究院，河南 洛阳 471000;2.63892部队，河南 洛阳 471003)

在空间拦截中，如果只通过拦截轨道设计使拦截器轨道和目标轨道产生碰撞点，拦截成功的概率是很低的，因为在拦截轨道设计中犹豫轨道计算误差、星历表数值误差等，实际很难同时到达理论碰撞点。因而要想实现高精度拦截就必须通过末制导技术以补偿轨道计算误差和其它各种非理想因素导致的误差。拦截器最终的摧毁效果主要取决于拦截器的制导精度和弹头的毁伤能力，提高拦截器的制导精度不仅可以增强拦截效果，还可以有效地降低拦截器的质量，提高弹头的机动性，从而更好地完成拦截任务。随着研究的深入，各种各样高性能的末制导律不断出现，近年来，非线性控制理论的研究不断深入，其中非线性逆系统理论是解决非线性问题的有力工具，它在很多领域都获得了广泛的应用。

逆系统方法是用反馈线性化方法来研究控制系统理论的一种途径，是一种比较有效的非线性制导控制方法。逆系统方法的基本思想是:用对象的模型构成一种可用反馈方法实现的原系统的“α阶积分逆系统”，将对象补偿为具有线性传递关系的且已经解耦的一种伪线性系统，然后利用线性系统的设计理论来完成对伪线性系统的综合控制［1］。

1 拦截的数学模型

拦截器和目标运动关系如图1所示。图中各参数分别定义如下:M表示拦截器，T表示目标，→r为弹目视线矢量，qθ为弹目视线倾角，qφ为弹目视线偏角，θm、θt分别为拦截器和目标的弹道倾角，φm、φt分别为拦截器和目标的弹道偏角。需要说明的是，以上关于倾角和偏角极性定义为按右旋规则绕相关坐标轴正方向旋转时为正，反之为负。θm、φm在图1中不易画出，故略去。

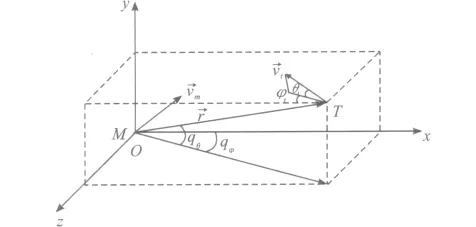
图1 拦截器和目标运动关系示意图

考虑到在拦截末段，拦截器和目标距离很近，攻击区狭窄，拦截器的横向运动是小量，所以cos(qφ－φm)≅1，于是弹目相对动力学方程可简化为［2～4］:

2 逆系统方法的一般理论

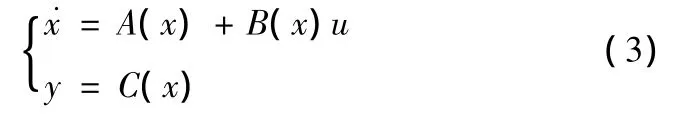
为例按照逆系统方法来研究其控制过程［6－7］。

式(3)中，x=(n×1)状态向量，u=(m ×1)控制向量，y=(l×1)输出向量，C=(l×n)常值矩阵。

此系统的逆系统是通过微分y的各分量足够次，直到含有u的关系式出现为止，由于只有m个输出能够被m个输入独立控制，所以假定m=l。引入K阶微分算子LKA(·)，其定义如下

现以一般仿射非线性系统

对原系统(3)施加逆动力学控制律(14)，则原系统变为解耦的线性动力系统

其中，W是新的外部输入。

3 基于逆系统方法的末制导律设计

4 数值仿真

取仿真参数如表1。

表1 基于逆系统方法的末制导律仿真参数

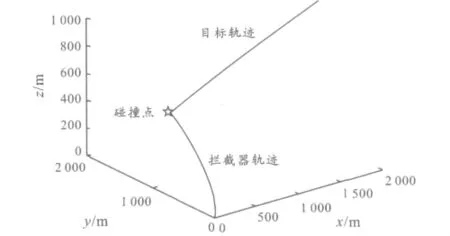
图4 拦截器和目标三维运动轨迹

脱靶量为 0.225 m，拦截时间为 2.97 s。

5 结束语

逆系统理论是解决非线性问题的有效方法，它通过伪线性化，进而利用线性系统理论进行控制系统设计。在本文中，通过选择合适的极点来满足控制系统的要求，从而实现精确制导。仿真结果显示，该制导律脱靶量小，制导精度高，这是因为在末制导律中采用了反映目标机动性的准确信息，但是该方法对于在系统模型不甚准确以及传感器测量精度不高的情况下，其鲁棒性相对较差。因此，将逆系统方法与鲁棒控制理论结合起来进行控制系统的设计，将是一个值得探讨的课题。

［1］ 李春文，冯元琨.多变量非线性控制的逆系统方法［M］.北京:清华出版社，1991:19－41.

［2］ Han Yanhua，Xu Bo.Variable Structure Guidance Law for Attacking Surface Maneuver Targets［J］.Journal of Systems Engineering and Electronics，2007，19(2):337 －341.

［3］ 刘暾，赵钧.空间飞行器动力学［M］.哈尔滨:哈尔滨工业大学出版社，2003.

［4］ 范东方.动能拦截器制导控制研究［D］.哈尔滨:哈尔滨工业大学硕士论文，2007.

［5］ Li-Ying Yuan，Shi-Yong Li.Missile Guidance Law Design Using Nonlinear Robust Output Regulation and T-S model［C］.2007 Second IEEE Conference on Industrial Electronics and Applications，2007:1037 －1042.

［6］ Fu-Kuang Yeh，Hsiuan-Hau Chien，Li-Chen Fu.Nonlinear Optimal Sliding Mode Midcourse Controller with Thrust Vector Control［C］.Proceeding of the American Control Conference，2002:1348 －1353.

［7］ 李君龙，胡振坤，胡恒章.一种基于逆动力学极点配置的空间拦截末制导律［J］.航天控制，1996(2):18－24.

［8］ 傅裕松，黄长强，翁兴伟，等.无人攻击机攻击低速目标的未制导律［J］.四川兵工学报，2011(4):12－14.

(责任编辑周江川)