多孔式翅片传热与流阻特性分析

王伟平 张淑文 杨 健 郑津洋 唐 萍 詹学华

(1浙江大学化工机械研究所 杭州 310027)

(2杭州杭氧股份有限公司 杭州 310004)

1 引 言

板翅式换热器具有传热效率高、结构紧凑以及适应性大等特点，广泛应用于空分、石化、制冷以及航空航天等领域。翅片是板翅式换热器的基本元件，传热过程主要通过翅片热传导以及翅片与流体之间的对流换热来完成，因此，翅片的表面特性是准确设计板翅式换热器的基础。自20世纪四五十年代以来，国内外学者对各类典型翅片(平直式、多孔式、锯齿式以及波纹式等)的表面特性进行了广泛的实验和理论研究［1-4］。近年来，随着计算机技术的发展，基于CFD的数值仿真技术已广泛应用于各类翅片表面性能的研究［5-8］。

多孔式翅片是在平直式翅片的基础上对翅片冲孔加工而成，翅片开孔可使热边界层不断破裂，从而提高其传热性能，同时也可促进流体间的横向混合，多用于导流板及流体中夹杂着颗粒或相变换热的场合。从已有的文献可知，CFD数值模拟技术主要应用于平直式、锯齿式以及波纹式翅片的研究，对多孔式翅片表面性能研究较少，主要停留在实验和理论分析阶段。本文结合CFD数值模拟技术，系统分析了不同孔口因素对多孔式翅片表面性能的影响，研究结果可望为多孔式翅片表面性能的提高提供参考。

2 模型与参数定义

2.1 物理模型

典型的多孔式翅片结构如图1所示，相关结构参数包括翅片长度L、翅片厚度δ、翅片间距S、翅片高度H、孔径d以及孔隙率σ等参数。

图1 典型多孔式翅片结构Fig.1 Schematic diagram of perforated fin

2.2 数值模型

采用商业软件Fluent进行数值模拟。相关设置包括:进出口边界条件选取质量流量进口和压力出口;压力-速度耦合求解选用SIMPLEC方法;流体流动若为层流-湍流过渡状态，采用SST过渡模型，若处于完全湍流状态，则选用标准K-eplison模型;质量守恒方程和动量守恒方程收敛于10－3，能量守恒方程收敛于10－4。本模拟的流动介质为空气，翅片材料为铝，相关物性参数如表1所示。

表1 流体介质与翅片的热力学参数Table 1 Thermodynamic parameters of fluid and perforated fin

为便于模拟，对模型做如下假设:

(1)各翅片通道相同，左右两侧壁面设为周期性边界，上下壁面设为恒温壁面，温度为353 K，初始流体进出口温度为293 K，如图2所示;

图2 多孔式翅片计算模型简图Fig.2 CFD model of perforated fin

(2)介质为稳态流动，忽略辐射换热，模拟过程中介质部分物性参数恒定;

(3)模型壁面呈理想状态，即翅片结构不存在毛刺和黏附物等影响介质流动的因素。

3 结果与讨论

评价多孔式翅片流动及传热性能主要参数分别为f因子(摩擦因子)和j因子(传热因子)。其中，f因子可通过式(1)获得:

式中:ΔP为翅片进出口压降;Dh为翅片进口水力直径;u为翅片进口速度;L为翅片长度。

j因子则由式(2)求得:

式中:Pr为普朗特数;Nu为努赛尔数，Nu=hDh/λ，参照文献［7－8］，传热系数h通过一系列公式迭代计算获得。

为便于数据分析和比较，依据文献［1］给出的几何尺寸，如表2所示，对图2模型进行模拟分析。

表2 多孔式翅片尺寸参数Table 2 Geometric parameters of perforated fin

3.1 CFD准确性验证

图3给出了同一孔隙率(σ=16%，d=2 mm)下，CFD模拟结果与已知实验数据［1，9］的对比情况。由于上述模型假设为翅片的理想状态，与实际实验工况存在差异，因此，CFD计算结果与实验值存在一定误差，但总体趋势较为吻合，如图3所示，一定程度上验证了将CFD技术应用于多孔式翅片表面性能研究的可行性。

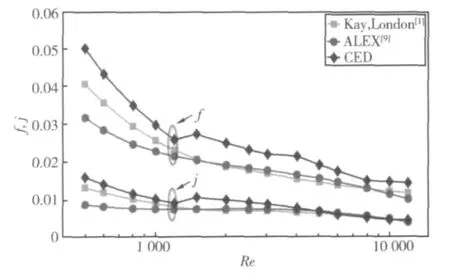
图3 CFD模型结果与实验数据对比Fig.3 Comparison of f and j values between CFD data and experiment data

3.2 多孔式翅片与平直式翅片比较

结合上述给出的基本模型，对平直式与多孔式翅片进行了建模分析，图4给出了两类翅片f因子与j因子的比较结果。低雷诺数下，由于流体处于层流状态，翅片打孔对流阻影响不大，随着雷诺数增加，空气侧流动变为紊流，流体流至孔口附近，将产生横向混合，引起周边流速的突然变化，从而形成气流漩涡与脱体运动，引起一定的压力损失，因此，过渡流或湍流状态下，多孔式翅片流阻大于平直式翅片，最大提高约15.75%(Re=2 500)。针对翅片的传热特性，由于带孔翅片主要增强了对气流的扰动，使湍流状态在较低雷诺数下提前达到，因此，层流-湍流过渡状态下，多孔式翅片对应的传热因子高于平直式翅片对应的传热因子，最大提高约14.27%(Re=12 000)，而在完全层流或充分湍流状态下，翅片打孔对强化传热影响不明显，图5为不同雷诺数下多孔式翅片较平直式翅片其流阻和传热性能的增长率情况。

3.3 孔隙率

图6、图7给出了同一雷诺数(Re=12 000)下，不同孔隙率(σ=1%—20%)和开孔直径(d=1.8 mm，d=2 mm，d=2.2 mm，d=2.5 mm)对多孔式翅片流阻和传热性能的影响。随着翅片开孔率的增加，流体间的横向混合增强，孔口周边的热边界层得到进一步破坏，一定程度上可提升翅片的流阻和换热性能，但由于开孔同时也导致了翅片换热面积的减少，因此，与翅片流阻相比，因孔隙率增加而引起的翅片换热性能的提升不够明显。由图6、图7可知，针对不同的开孔直径，当孔隙率从1%增加至20%，翅片f因子大约增加65.17%—73.72%，而j因子则大约仅增加6.29%—7.01%。另外，当孔隙率一定时，随着孔径减少，由于翅片表面分布的孔口增多，对流体影响的区域扩大，因此，对应的翅片传热性能和流阻也得到一定提升。

3.4 孔口布置方式

图8给出了同一孔隙率(σ=10%)和孔口直径(d=2 mm)下，孔口布置呈并行布置和错列布置方式对多孔式翅片流阻与传热的影响。由于堵塞作用的影响，翅片呈错列布置时，其对应的流阻较翅片孔口呈并行布置时对应的流阻大，最大提高约24.61%(Re=2 500)。由于流体的混合作用，错列孔口布置对应的传热性能高于并行孔口布置对应的传热性能，最大提高约14.69%(Re=2 500)。

3.5 开孔类型

多孔式翅片常用开口形状包括圆形、正三角形以及正四方形等3种类型，图9给出了同一孔隙率(σ=4.9%)和单孔面积(3.14 mm2)下，不同开孔形状对翅片流阻和传热特性的影响。由图9可知，层流状态下，孔口结构为正四方形的多孔式翅片流阻大于孔口结构为正三角形和圆形的多孔式翅片流阻;湍流状态下，开孔形式对翅片流阻影响则小。不同开孔结构对多孔式翅片传热性能影响则较小，可忽略不计。

图8 孔口布置对多孔式翅片f因子和j因子的影响Fig.8 Effects of perforation layout on f and j values in perforated fin

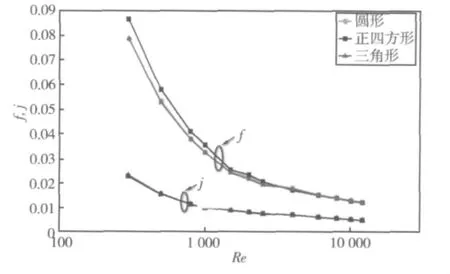
图9 孔口形状对多孔式翅片f因子和j因子的影响Fig.9 Effects of perforation shape on f and j values in perforated fin

4 结 论

结合已有的实验数据和理论方法，采用CFD数值分析技术对多孔式翅片进行了模拟研究，对比分析了不同孔口因素对其传热和流阻特性的影响，获得如下结论:

(1)层流状态下，多孔式翅片流阻与平直式翅片近似，过渡流或湍流状态下，多孔式翅片流阻大于平直式翅片对应的流阻。完全层流或充分湍流状态时，多孔式翅片的传热性能与平直式翅片类似，当流体呈过渡状态时，其传热性能高于平直式翅片;

(2)随着孔隙率增加，多孔式翅片流阻增加，其传热性能得到一定提升但不显著。同一孔隙率下，随着孔径减少，多孔式翅片的传热性能和流阻得到一定提升;

(3)多孔式翅片开孔方式呈错列布置时，其对应的流阻与传热性能高于开孔方式呈并行布置的多孔式翅片;

(4)层流状态下，孔口结构为正四方形的多孔式翅片，其流阻大于孔口结构为正三角形和圆形的多孔式翅片流阻，湍流状态下，孔口结构对翅片流阻影响则较小。不同开孔结构对多孔式翅片传热性能影响较小，可忽略不计。

1 Kays W M，London A L.Compact heat exchangers［M］.New York:McGraw-Hill，1984.

2 Liang C Y，Yang W J.Heat transfer and friction loss performance of perforated heat exchanger surfaces［J］.Journal of Heat transfer，1975，97(1-9):9-15.

3 Joshi H M，Webb R L.Heat transfer and friction in the offset strip fin heat exchanger［J］.International Journal of Heat and Mass Transfer，1987，30(1):69-83.

4 Manglik R M，Bergles A E.Heat transfer and pressure drop correlations for the rectangular offset strip fin compact heat exchanger［J］.Experimental Thermal and Fluid Science，1995(10):171-180.

5 Ismaila L S，Velraj R.Studies on fanning friction(f)and colburn(j)factors of offset and wavy fins compact plate fin heat exchanger-a CFD approach［J］.Numerical Heat Transfer，2008，56:987-1005.

6 Kim M S，Lee J，Yook S J，et al.Correlations and optimization of a heat exchanger with offset-strip fins［J］.International Journal of Heat and Mass Transfer，2011，54(9-10):2073-2079.

7 Peng H，Ling X.Numerical modeling and experimental verification of flow and heat transfer over serrated fins at low Reynolds number［J］.Experimental Thermal and Fluid Science，2008，32(5):1039-1048.

8 Zhu Y H，Li Y Z.Three-dimensional numerical simulation on the laminar flow and heat transfer in four basic fins of plate-fin heat exchangers［J］.Journal of Heat Transfer，2008，130(11):111801(1-8).

9 陈长青，沈裕浩.低温换热器［M］.北京:机械工业出版社，1993.