高阶多智能体网络在固定和动态拓扑下的一致性分析

于镝，伍清河，王寅秋

(1.北京理工大学 自动化学院，北京100081;2.东北石油大学 电气信息工程学院，黑龙江 大庆163318)

0 引言

近些年来，随着智能化武器在军事领域地位的日益提升，多智能体协调控制已成为复杂控制研究中十分活跃的领域。其相关技术广泛应用于多机器人、无人机、军用车辆和卫星编队控制以及空中交通控制和军事搜寻等非编队控制。在协调控制中，为完成复杂任务或实现共同目标，智能体之间需相互影响且最终在协调数据上达成一致。在已有文献中，称智能体的状态收敛到共同值为一致性问题，这是协调控制中的重要研究课题，已受到学者们的极大关注。

目前大多数成果均限于个体动态为一阶积分器［1－5］和二阶积分器［6－11］网络的一致性分析，但关于高阶网络一致性的研究成果很少。高阶网络一致性问题的研究动机部分来源于群体行为的观察。譬如协调作战的无人机组，迫于环境变化突然改变运动方向，此时不但要求位置和速度的一致，而且要求加速度的协调统一。因此高阶多智能体网络一致性的研究具有重要的理论及现实意义。Ren 和Wang均从特征方程入手，讨论有向固定拓扑网络的Laplacian 阵特征值与整个闭环网络系统矩阵的特征值之间的对应关系，从而给出一致性条件［12－13］。而Lin 采用模型变换的方法，在一定条件下，将系统矩阵变换为随机矩阵，进而应用非负矩阵理论得出高阶有向动态离散网络渐近一致性条件［14］。

本文的主要贡献是将一阶有向网络的一致性分析结果［4－5］拓展到高阶情况。首先对网络系统进行模型变换，将由M 个n 阶子系统所构成的网络等价地变换为由nM 个一阶子系统所构成的网络。在一定条件下，变换后的网络系统矩阵为具有零行和的Metzler 矩阵，从而建立起网络系统矩阵与网络拓扑的Laplacian 矩阵之间的对应关系。由此给出高阶有向网络一致性分析的新结果。从图论的角度出发，得到了原网络拓扑有生成树与模型变换后的网络拓扑有生成树两者等价的结论。针对固定拓扑，分别给出无领航和领航－跟随两种情况下一致性条件及一致状态。并且基于非负矩阵理论证明在有限的拓扑切换时间间隔内，若有向图联合具有生成树，则整个闭环网络实现渐近一致。与文献［6］相比，放宽了对网络拓扑和拓扑切换停留时间的限制。最后应用多车辆编队控制仿真进行理论验证。

1 系统模型和问题描述

考虑M 个n 阶智能体所构成的网络，第i 个智能体的动态描述如下:

其中:ξi(t)∈R 为智能体i 的信息变量…，n－1 为ξi(t)的k 阶导数;ui(t)∈R 为控制输入，初始条件为设分别为智能体i 的状态和初始状态，分别表示整个多智能体网络的状态和初始状态。

本文要解决网络(1)的下列一致性问题:

定义1 考虑由动态(1)描述的智能体所构成的网络，若在任意的初始条件下，智能体的状态满足

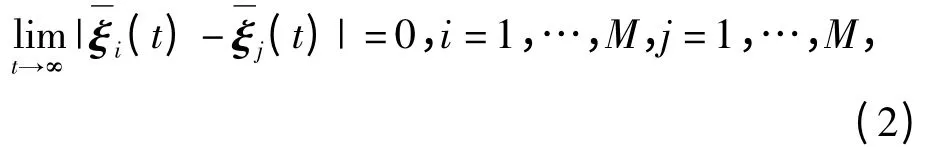
则称整个多智能体网络实现了渐近一致。而且，若存在ξ*(t)∈Rn，都有

则称ξ*(t)是网络的一致状态。

为解决上述一致性问题，我们选取下列分布式一致性协议

其中，i=1，…，M，γk＞0，k =1，…，n－1 是绝对信息的反馈增益，β 是相对信息的反馈增益，Ni是智能体i 的邻居集合，aij(t)表示时变的邻接矩阵元素。协议(4)的目的是使M 个智能体的信息变量趋于一致，而其各阶导数趋于0.

基于协议(4)，第i 个智能体的动态可描述为

其中，L(t)是有向图G［3］所对应的Laplacian 阵。

2 模型变换

本节对闭环网络进行模型变换，并分析变换前后网络拓扑之间的关系。

si∈P，i=1，…，n－1，P 是由正数构成的有限集。令模型变换后整个闭环网络的状态和初始状态分别为则网络动态为

其中:

则可以把一阶一致性算法的收敛性分析结果拓展到高阶系统的一致性分析中来。有如下引理

引理1 在满足条件(8)的情况下，－Ψ(t)是整个闭环网络(7)的Laplacian 矩阵。

设模型变换后的闭环网络拓扑对应的有向图为G'(V'，ε'，A')，其中顶点集V' ={v'1，…，v'nM}，边集ε'⊂V' ×V'，A'(t)=［a'ij(t)］∈ℝnM×nM为加权邻接矩阵，其中a'ij(t)≥0.则－Ψ(t)=［φij］∈ℝnM×nM，其中φii= ∑j≠ia'ij，φij=－a'ij.原拓扑和模型变换后拓扑有如下等价关系。

定理1 在满足条件(8)的情况下，有向图G'有生成树的充要条件是有向图G 有生成树。

证明:由引理1 得，－Ψ(t)对应的邻接矩阵为

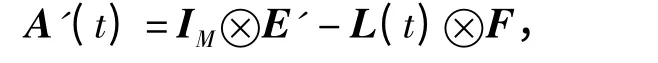
其中，

可知节点vin+1到节点v(i+1)n，i =0，…，M－1 是强连接的，且节点vin只可能得到节点v1，…，v(i－1)n+1，vin+1，v(i+1)n+1，…，v(M－1)n+1的信息，i =1，…，M－1.则整个网络可以看成由M 个强连通分量以及它们之间的连接拓扑组成，如下图所示。

图1 模型变换后的闭环网络拓扑图Fig.1 Topology of network after model transformation

充分性:若有向图G'的M 个强连通分量之间有生成树，则G'一定有生成树。将有向图G'的强连通分量所对应的边删除后的邻接矩阵为

可见当有向图G 有生成树，则有向图G'的M 个强连通分量之间有生成树，所以G'一定有生成树。

必要性:将每个强连通分量收缩看成一个节点，则当G'有生成树，则G 一定有生成树。

3 固定拓扑下的一致性分析

本节考虑网络(6)在固定拓扑下的一致性分析，并分别讨论无领航、领航－跟随两种情况。

引理2［5］设L 是有向图G 所对应的Laplacian矩阵。当且仅当有向图G 有生成树时，L 有一单零根，而其余特征根具有正实部。而且存在零特征根的左、右特征向量νTl=［ν1，…，νM］和1n，满足L1n=0 和νTlL=0，并且νTl1n=1，其中νi＞0，i=1，…，M.

基于上述结果，根据文献［4］，得出无领航情况下网络(6)渐近一致的充分条件。

定理2 在满足条件(8)的情况下，若有向图G有生成树，则高阶多智能体网络(6)在固定拓扑下可实现渐近一致。而且闭环网络一致状态为χ(ξ0)e1，其中ℝn，和ξ0的含义同前所述。证明:固定拓扑下，网络(7)的系统矩阵为Ψ=IM⊗E－L⊗F.由已知条件和定理1 可得，有向图G'有生成树。所以高阶多智能体网络(7)的系统矩阵Ψ 有一单零根，且其余特征根具有负实部，即λ1(Ψ)=0，Re(λi(Ψ))＜0，i =2，…，nM.则存在非奇异变换T，使得

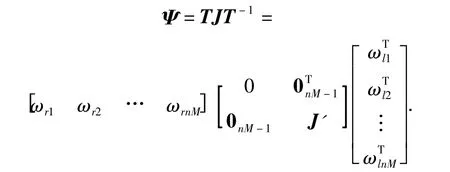
其中，J'为λi(Ψ)，i=2，…，nM 所对应的约当块，和ωr1分别为零特征根的左、右特征向量。由于

则由η=(IM⊗S)ξ 可得

在实际应用中，大部分情况下要求每个智能体的状态随时间变化。例如在车辆编队控制中，不但要求车辆间保持一定的编队队形，而且一致状态可能由一个参考状态确定，或为车辆或环境动态的时变函数。因此，有必要讨论领航—跟随一致性。

假设存在一个虚拟领航者，其动态描述为

设领航者状态为ξ*(t)=［ξl(t)…ξnl－1(t)］T.若要求各智能体的位置之间保持一定距离，可给出协议

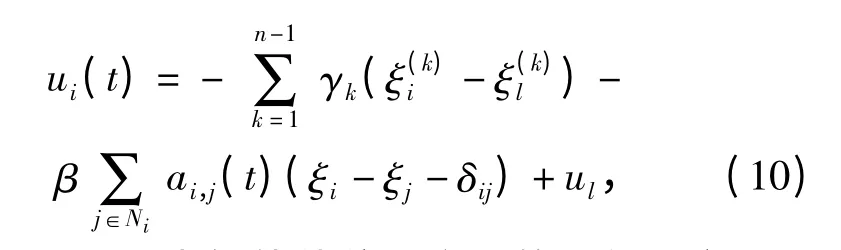
其中，δij=δi－δj为智能体位置之间的期望距离。

推论1 假设所有智能体都已知虚拟领航者的状态。在满足条件(8)的情况下，若有向图G 有生成树，则在固定拓扑下，网络(6)在协议(10)的作用下可渐近实现ξi(t)→χ(ξ0)+ξl(t)+δi，即ξi(t)－ξj(t)→δij，且ξ(k)i(t)→ξ(k)l(t)，i=1，…，M，j=1，…，M，k=1，…，n－1.

证明:令ζi(t)=ξi(t)－δi－ξl(t)，i =1，…，M为高阶网络的状态变量，按照定理2 的证明思路得证。

4 动态拓扑下的一致性分析

在实际应用中，由于外部干扰，或数据传输丢包和通信时滞，使得智能体之间的通信连接间断，从而导致网络拓扑发生变化。所以本节考虑闭环网络(6)在动态拓扑下的一致性分析。

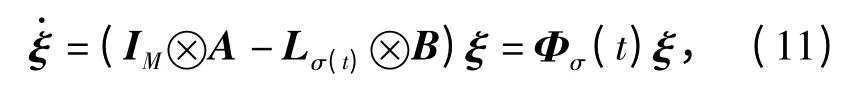
在给出主要结论之前，先给出如下引理。

引理3［15］设W1，W2，…，Wk∈ℝp×p是SIA 矩阵的有限集，且其中每个有限序列Wi1，Wi2，…，Wij的乘积是SIA 矩阵。则对每个无限序列Wi1，Wi2，…，都存在一个列向量y∈ℝp使得

定理3 设t0，t1，…是一个无限时间序列，网络拓扑在这些时刻发生切换。并且0 ＜ti+1－ti≤τi，i=0，1，2，…，τi∈ℝ+，其中t0是初始时刻。在满足条件(8)的情况下，若在每个时间间隔［tij，tij+1)，j =0，1，…内，其中ti0=t0，有向图Gtij，Gtij+1，…，Gtij+1－1联合具有生成树，则闭环网络(6)实现渐近一致。

证明:

2)设k 是满足时间条件tk＜t 的最大非负整数，则闭环网络(7)的状态为

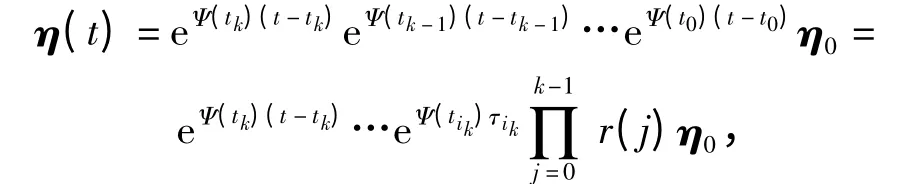
其 中，r (j)= eΨ(tij+1－1)τij+1－1… eΨ(tij+1)τij+1eΨ(tij)τij，Ψ(tij)，Ψ(tij+1)，…，Ψ(tij+1－1)分别是有向图G'tij，G'tij+1，…，G'tij+1－1所对应的系统矩阵。在满足条件(8)的情况下，若在每个时间间隔［tij，tij+1)，j =0，1，…内，其中ti0=t0，有向图Gtij，Gtij+1，…，Gtij+1－1联合具有生成树，则由定理1 得，有向图G'tij，G'tij+1，…，G'tij+1－1联合具有生成树。根据文献［5］中的引理3.11 可得r(j)=eΨ(tij+1－1)τij+1－1…eΨ(tij+1)τij+1eΨ(tij)τij是SIA.而且，在时间间隔［tij，tij+m)，j=0，1，…内，有向图Gtij，Gtij+1，…，Gtij+m－1的并有生成树，所以(l)也是SIA.则由引理3 得

3)由eΨ(tik)τik，…，eΨ(tk)(t－tk)均为随机矩阵，得

因为η=(IM⊗S)ξ，则

其中，k=1，…，n－1，i=1，…，M.即闭环网络(6)实现渐近一致。

5 仿真

针对由4 个三阶智能体Σ1－Σ4所构成的有向网络分别进行固定拓扑和动态拓扑的仿真研究。当智能体个数增多以及个体动态阶次n ＞3 时，结论同样成立。为了满足条件(8)，并考虑渐近一致收敛速度，令参数E3，1=3，E3，2=1，E3，3=－4，s1=s2=1.通过计算得出γ1=8，γ2=6.

固定拓扑图如图2所示。当相对信息的反馈增益取β=1 和β=2 时，仿真图形如图4和图5所示。由仿真结果知所有智能体的第一个状态变量渐近达成一致，而其它两个状态变量渐近收敛到零，与定理2 的结论相符合。并且β 值越大，收敛速度越快。

图2 有向固定拓扑图Fig.2 Directed fixed topology

切换拓扑图如图3所示。为了模拟拓扑切换，设网络拓扑每隔0.2 s 按G1→G2→G3→G4→G1进行切换。在每个拓扑切换周期0.8 s 内，有向图的并有生成树。令协议中参数γ1=8，γ2=6，β =2，仿真图形如图6所示。同样所有智能体的状态变量均达成渐近一致，与定理3 的结论相符合。

图3 有向图G1－G4Fig.3 Directed graph G1－G4

在此基础上，进行编队控制的仿真研究。令4个智能体分别代表4个车辆，要求它们保持一个期望的菱形编队队形，且虚拟领航者即编队中心按时变轨迹ξl(t)=［10cost，10sint］T的规律变化。采用

图4 固定拓扑下(β=1)智能体状态变量轨迹Fig.4 Trajectories of state variables of agents in fixed topology when β=1

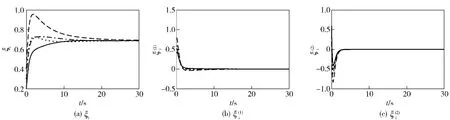
图5 固定拓扑下(β=2)智能体状态变量轨迹Fig.5 Trajectories of state variables of agents in fixed topology when β=2

图6 切换拓扑下智能体状态变量轨迹Fig.6 Trajectories of state variables of agents in switching topology

图7 固定拓扑下的编队队形变化Fig.7 Formation configuration change in fixed topology

图8 切换拓扑下的编队队形变化Fig.8 Formation configuration change in switching topology

分布式协议(10)，固定拓扑和切换拓扑如前所述，编队仿真图形如图7和图8所示。图7显示4 个车辆在固定拓扑情况下，t∈{5 s，25 s，30 s，40 s，55 s}时的编队图形。可见经过大约20 s，其编队中心跟随上时变轨迹的变化;经过大约50 s，车辆间保持期望的编队队形。图8显示在切换拓扑情况下，t∈{1 s，50 s，100 s，125 s，200 s}时4 个车辆的编队图形。可见经过大约125 s 的协调控制，车辆不但能保持期望的编队队形，而且其编队中心跟随上时变轨迹的变化。

6 结论

本文针对高阶多智能体网络首先进行模型变换，在一定条件下，得到系统矩阵为具有零行和Metzler 矩阵的一阶网络。基于系统矩阵与网络拓扑的Laplacian 矩阵之间的对应关系，将一阶有向网络的一致性分析结果拓展到高阶情况，从而给出高阶有向网络一致性分析的新结果。不同于文献［14］，从图论角度出发，更直观的得到原网络拓扑有生成树与模型变换后的网络拓扑有生成树两者等价的结论。针对固定拓扑，分别给出无领航和领航－跟随两种情况下一致性条件及一致状态。并且基于非负矩阵理论证明在有限的拓扑切换时间间隔内，若有向图联合具有生成树，则整个闭环网络实现渐近一致，从而放宽了对网络拓扑和拓扑切换停留时间的限制。最后应用多车辆编队控制仿真进行理论验证。由于实际的物理系统经常受到外界干扰、未建模动态等不确定因素的影响，对具有不确定性的高阶网络一致性的分析是下一步的研究内容。

References)

［1］ Vicsek T，Czirok A，Ben－Jacob E，et al.Novel type of phase transition in a system of self－driven particles［J］.Physical Review Letters，1995，75(6):1226－1229.

［2］ Jadbabaie A，Lin J，Morse A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules［J］.IEEE Transactions on Automatic Control，2003，48(6):988－1001.

［3］ Olfati－Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time－delays［J］.IEEE Transactions on Automatic Control，2004，49(9):1520－1533.

［4］ Ren Wei，Beard R W，McLain T W.Coordination variables and consensus building in multiple vehicle systems［M］∥Lecture Notes in Control and Information Sciences，New York:Springer－Verlag，2004:171－188.

［5］ Ren Wei，Beard R W.Consensus seeking in multi－agent systems under dynamically changing interaction topologies［J］.IEEE Transactions on Automatic Control，2005，50(5):655－661.

［6］ Ren Wei，Beard R W.Distributed consensus in multi－vehicle cooperative control:theory and applications［M］.London:Springer，2008:89－96.

［7］ Tanner H G，Jadbabaie A，Pappas G J.Flocking in fixed and switching networks［J］.IEEE Transactions on Automatic Control，2007，52(5):863－868.

［8］ Xie Guangming，Wang Long.Consensus control for a class of networks of dynamic agents［J］.International Journal of Robust and Nonlinear Control，2007，17:941－959.

［9］ Lin Peng，Jia Yingmin.Consensus of second－order discrete time multi－agent systems with nonuniform time－delays and dynamically changing topologies［J］.Automatica，2009，45:2154－2158.

［10］ Olfati－Saber R，Fax J A，Murray R M.Consensus and cooperation in networked multi－agent systems［J］.Proceedings of the IEEE，2007，95(1):215－233.

［11］ Ren Wei，Beard R W，Atkins E M.Information consensus in multivehicle cooperative control［J］.IEEE Control System Magazine，2007，6:71－82.

［12］ Ren Wei，Moore K，Chen Yangquan.High－order and model reference consensus algorithms in cooperative control of multi－vehicle systems［J］.ASME Journal of Dynamic Systems，Measurement，and Control，2007，129(5):678－688.

［13］ Jiang Fangcui，Wang Long，Jia Yingmin.Consensus in leaderless networks of high－order－integrator agents［C］∥Proceedings of American Control Conference，St.Louis，2009:4458－4463.

［14］ 林鹏.多智能体系统一致性控制及其在编队中的应用［D］.北京:北京航空航天大学，2009:65－69.LIN Peng.Consensus control of multi－agent systems and its applications to formations［D］.Beijing:Beihang University，2009，65－69.(in Chinese)

［15］ Wolfowitz J.Products of indecomposable，aperiodic，stochastic matrices［C］∥Proceedings of the American Mathematical Society，1963:733－736.