一种极化捷变雷达中欺骗性干扰的提取方法

陈歆炜，赵建中，吴文

(南京理工大学 近程高速目标探测技术国防重点实验室，江苏南京210094)

0 引言

欺骗性干扰采用虚假目标信息作用于雷达的目标检测和跟踪系统，迷惑和扰乱雷达对真正目标的检测和跟踪［1］。当干扰机极化方式相对固定时，极化捷变雷达可在工作中灵活改变发射或接收电磁波的极化方式，并在极化轨道约束下实现信号干扰噪声比(SINR)和信号干扰功率差(PDSI)的最优化，且改善信号接收效果的有效度超过1/2［2－4］.为了优化上述极化滤波的效果，文献［5］在已知目标回波和干扰信号Jones 矢量的基础上对干扰信号和目标回波信号的椭圆描述子参数直接进行实数加权，实现了目标回波极化状态与干扰极化状态在Poincare 极化球上的分离，使系统的抗干扰能力提高了15.4%～100%.因而干扰信号的提取及其参数的获取在极化雷达的信号处理中具有重要意义，且干扰Jones 矢量计算的精确性是决定系统抗干扰性能的重要因素之一。

目前，尚无关于计算干扰Jones 矢量的相关文献发表，但已有不少信号处理方法对干扰信号的特征进行提取。Liang 等分别将幅度归一化和未归一化的同一信号进行小波变换，在滤除峰值后根据两路输出谱线的方差来判别信号的调制方式，但将同一信号分成两路计算的方式增加了系统处理负担［6］。李建勋等运用Kohonen 网络通过对输入模式进行学习，神经元在空间形成不同的聚类来区分雷达回波中目标和干扰的不同时频谱特征，然而实现该方法时需预先对神经网络进行数百步训练［7］。上述方法的基本原理都是通过对采样信号的某种变换，使信号之间特征区分明显，从而为分类识别奠定基础。

为简化目标回波和干扰信号的分离过程以及求解干扰的Jones 矢量，本文运用极化捷变技术发射一组极化方式相互关联的脉冲信号，利用目标极化散射特性以及干扰极化相对不变特性，使目标回波在信号运算中实现与干扰信号的分离，从而获得干扰波形，并能准确计算其Jones 矢量。该方法易于实现，并基于常用的脉冲雷达系统设计了干扰提取流程，与现有干扰特征提取算法相比，可节省FPGA的芯片资源(逻辑单元和存储空间)。最后给出了Matlab 仿真结果和Jones 矢量计算误差与干噪比(INR)、信干比(SIR)的关系曲线。

1 干扰信号提取算法

1.1 极化空间中的干扰和目标回波

经典电磁极化学理论表明，Poincare 极化球是表征极化状态非常有效的工具。任何一个单色波都可以用极化球上的一点来完全的表征，并且球上的点集囊括了所有可能的极化状态。可以将Poincare极化球上表示的所有点的集合表示为极化空间P.

极化捷变雷达中发射信号的极化方式可以在某范围内变化，一系列的点集构成了发射信号集合T，即

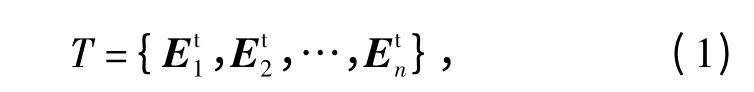
式中:Etn为第n 次发射的电磁波Jones 矢量。发射信号集合是极化空间的子集，满足T⊆P.

本文取水平极化(H)和垂直极化(V)作为Jones矢量的基，根据电磁学散射理论，雷达天线发射电磁波Et与接收电磁波Er之间的归一化关系可表示为

即

当雷达发射的电磁波极化方式改变时，目标回波的极化方式就会依照式(3)的关系作相应改变。一系列目标回波的Jones 矢量组成了回波信号集合R，即

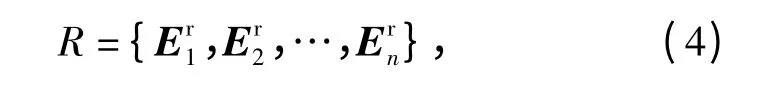
式中:Ern为第n 次发射电磁波Etn后目标回波的Jones 矢量。同样，回波信号集合也是极化空间的子集，即R⊆P.

由式(2)或式(3)的关系可以看出，雷达发射信号集合T 与目标回波信号集合R 之间满足一种映射关系，即

本文针对干扰机极化方式相对固定的情况进行讨论［8］。此时，干扰信号的Jones 矢量在一定时间内可认为是不变的，由该矢量构成的干扰信号集合I 仅包含一个元素，即

式中:Ei为干扰信号电磁波的Jones 矢量。

根据集合T、集合R 和集合I 之间的关系，可得到图1所示的文氏图。图中I 是空间P 内任意一点，有可能包含于T 或者R.

由图1可以看出目标回波的极化方式会随着发射信号极化的变化而改变，而干扰的极化则是不变的。发射几组预定的相关信号，目标回波极化方式会按照规律改变，然后通过信号之间的运算可将目标回波分离，提取出干扰信号。下文将阐述干扰提取的具体过程。

图1 信号、干扰和极化空间的关系Fig.1 The relation between signal，deception and polarization space

1.2 干扰提取算法

干扰信号提取分以下几个步骤进行:

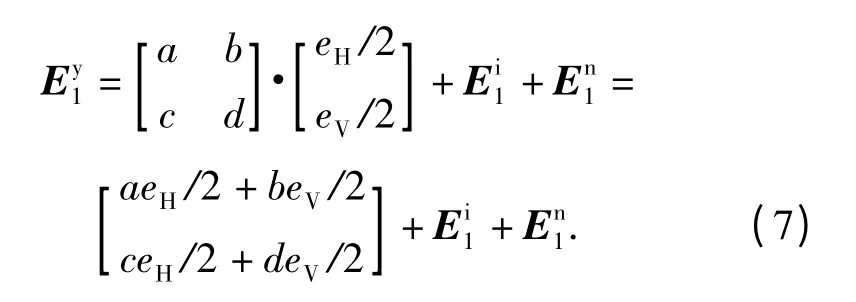
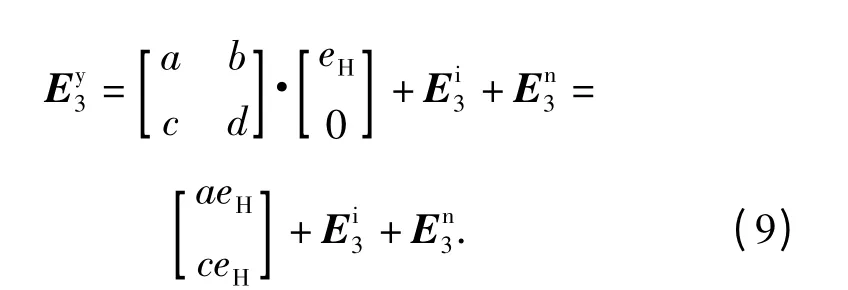
4)做信号运算E1y+ E2y－ E3y，根据式(7)、式(8)、式(9)，且考虑到E1i=E2i=E3i，有

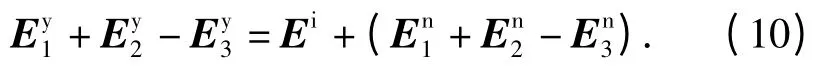
5)在所得干扰和噪声混合信号的基础上完成特征识别及参数提取的运算［9］，即获得干扰信号的各项参数。

由上述运算过程可以看出，目标回波信号在极化捷变过程中发生了相应改变，当目标姿态在这过程中没有较大变化(目标散射矩阵相对不变)时，可认为通过该算法中简单的加减运算已把目标回波信号完全消去。

对于噪声中正弦干扰信号Jones 矢量的计算，可采用文献［10］的方法进行两通道相位差计算，并用类似的自相关方法进行各通道信号幅度的计算。

2 系统实现

上文所提干扰信号的提取和Jones 矢量的计算方法可在普通双极化雷达数字发射/接收机中实现。为了实现极化捷变的功能，发射机需采用相位捷变多路信号源［11］，并在前端安装开关部件。系统构架框图如图2所示。

图2 干扰提取系统框图Fig.2 The block diagram of deception extracting system

系统发射机前端在控制单元的控制下，改变双通道的输出信号的幅度和相位，使发射的电磁波极化方式按照算法规律改变。双极化接收前端将接收到的目标回波和干扰的混合信号转为中频，经A/D采样进入后端处理。系统处理单元进行相应运算后即可输出干扰的波形和参数。干扰参数提取运算可按如下所示的流程进行。

图3 干扰参数提取流程图Fig.3 The flow chart of deception extracting

在实际运用中，可多次重复上述过程，以获得较为准确的结果。该方法中只需完成信号的简单加减运算便可将干扰信号提取出来;信号特征提取及Jones 矢量的计算也只需进行信号的相关或FFT 运算［9－10］。表1所示为相关的算法在运算量大致相同时消耗FPGA 资源的对比情况。

表1 各算法消耗FPGA 资源对比Tab.1 A comparison between several algorithms in FPGA resources

由表1可以看出，比起小波分析、神经网络等复杂的信号处理算法，该方法中所使用的相关运算和FFT 运算在单片实现时可节省FPGA 芯片资源。

3 仿真及分析

本文在Matlab 的Simulink 环境中按图2所示系统结构搭建了仿真平台，对干扰的提取和Jones矢量的计算进行仿真。仿真中，雷达工作在脉冲体制下。假设某固定目标散射矩阵为 S =连续波干扰信号Jones 矢量为Ei=在INR 为11.85 dB(水平通道)、17.34 dB(垂直通道)及SIR 为－4.29 dB(水平通道)、－4.71 dB(垂直通道)的条件下，有如图4～图6所示的仿真结果。

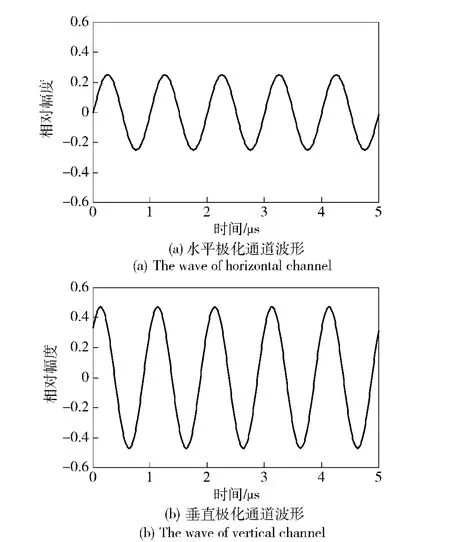
图4 干扰信号原始波形Fig.4 The original waves of deception

根据提取到的干扰波形，可计算得该干扰的Jo nes 矢量为改变干扰参数进行仿真，结果如表2所示。

表2中结果的误差是由噪声引起的随机误差以及计算时的量化误差和截断误差造成的。在误差允许的范围内(相对误差≤10%)，计算得到的干扰信号Jones 矢量与原参数基本一致。

图5 接收机输出波形(3 次脉冲)Fig.5 The waves output by receiver (3 pulses)

当目标、发射信号和干扰信号功率不变且双通道SIR=2 dB 时，改变噪声功率大小，可得到如图7所示的Jones 矢量计算的相对误差与INR 之间的关系;当目标、干扰信号和噪声功率不变且双通道INR=12 dB 时，改变发射信号功率大小，可得到如图8所示的Jones 矢量计算的相对误差与SIR 之间的关系。

表2 不同干扰参数下仿真结果Tab.2 The simulation results of different situations

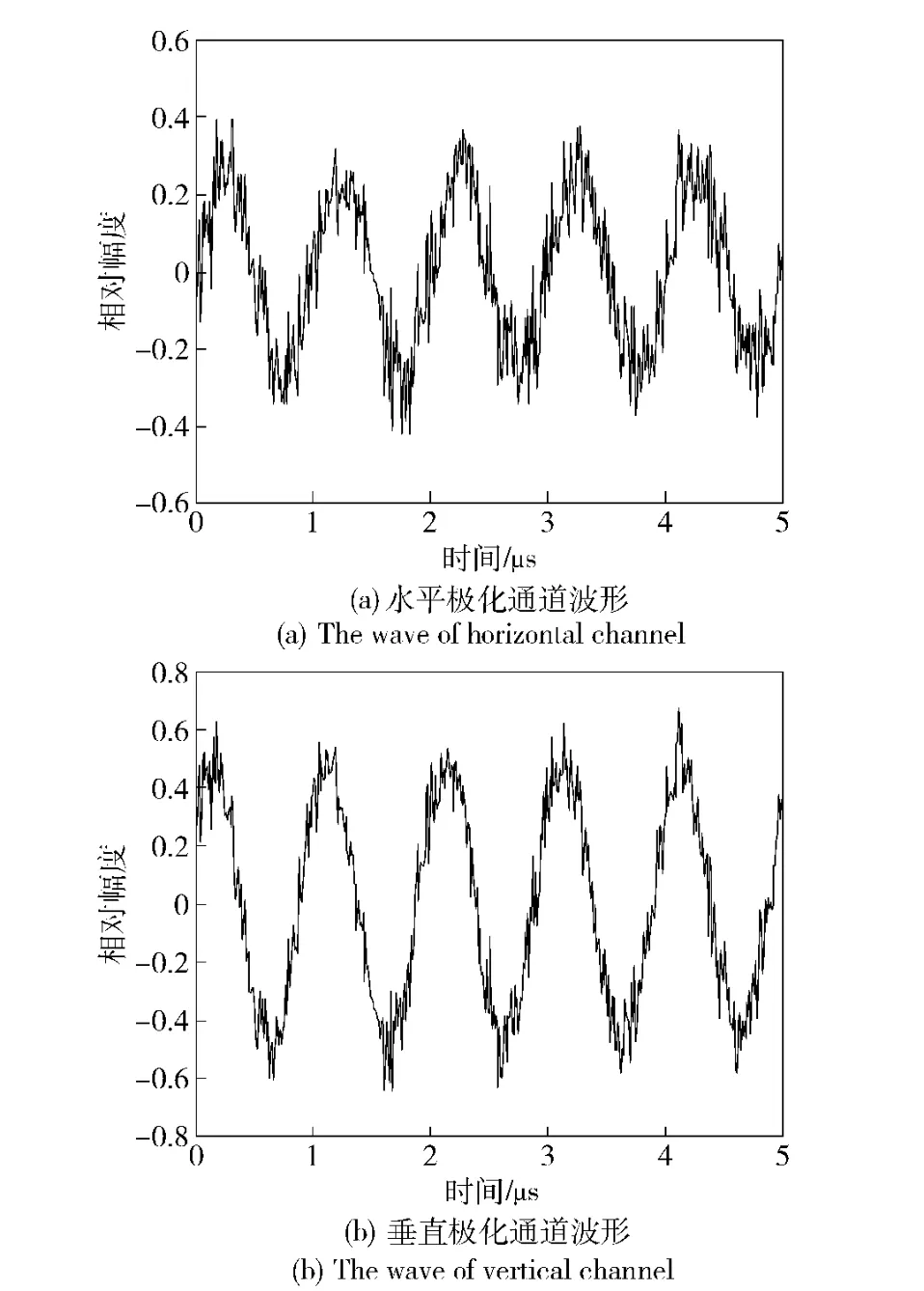
图6 提取后得到的干扰信号波形Fig.6 The waves of extracted deception

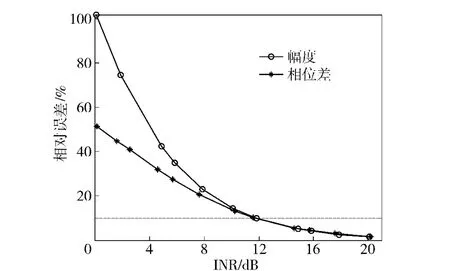
图7 干扰的Jones 矢量计算的相对误差与INR 的关系Fig.7 The relationship between relative errors of Jones vector of deception calculation and INR

由图7可以看出，当系统INR 较低时，由于噪声功率较大，计算时出现较大误差;当INR 大于11.8 dB 时，计算结果与原信号参数之间相对误差小于10%，可应用于后续的干扰分析及抗干扰处理。由于本文算法能够滤除目标回波信号，因此图8所示目标回波信号功率对干扰Jones 矢量的计算基本没有影响，误差曲线只在噪声不一致的影响下作小幅波动。当干扰与信号分离后，按照文献［9］所述特征参数提取方法，可在INR 低至－9 dB 时达到对干扰特征识别100%的正确率，优于文献［6－7］中的特征识别结果。详细的对比情况如表3所示。

图8 干扰的Jones 矢量计算的相对误差与SIR 的关系Fig.8 The relationship between relative errors of Jones vector of deception calculation and SIR

表3 本文所得结果与其他相似文献中结果对比情况Tab.3 The comparisons of the results get from this paper with the results get from other papers

4 结论

本文提出的一种简便实用的雷达欺骗性干扰信号提取方法，能在极化捷变雷达发射数次脉冲后消去目标回波信号，将干扰分离，从而可计算出干扰的详细参数(Jones 矢量)。该方法易于实现，且可比类似干扰提取方法节约FPGA 芯片资源。在系统具有足够INR 时能较准确地计算干扰信号的Jones 矢量。该方法为极化雷达的后续的抗干扰处理提供了必要条件和重要参考。

References)

［1］ 粟苹.信息对抗技术［M］.北京:清华大学出版社，2008:59－60.SU Ping.Warfare technology［M］.Beijing:Tsinghua University Press，2008:59－60.(in Chinese)

［2］ YANG Yun－fu，WANG Zhao－hui，TAO Ran，et al.Optimal polarization for SINR equation in partially polarized case［C］∥IEEE 2007 International Symposium on Microwave，Antenna，Propagation and EMC Technologies for Wireless Communications.Piscataway:IEEE，2007:1420－1423.

［3］ 王雪松，徐振海，代大海，等.干扰环境中部分极化信号的最佳滤波［J］.电子与信息学报，2004，26(4):593－597.WANG Xue－song，XU Zhen－hai，DAI Da－hai，et al.Optimal filtering of partially polarized signals in the interference background［J］.Journal of Electronics and Information Technology，2004，26(4):593－597.(in Chinese)

［4］ 庄钊文，肖顺平，王雪松.雷达极化信息处理及其应用［M］.北京:国防工业出版社，1999:293－377.ZHUANG Zhao－wen，XIAO Shun－ping，WANG Xue－song.Radar polarization information processing and application［M］.Beijing:National Defense Industry Press，1999:293－377.(in Chinese)

［5］ 张国毅，刘永坦.实数加权极化变换法［J］.电子学报，2000，28(3):69－72.ZHANG Guo－yi，LIU Yong－tan.Real weighting polarization vector translation［J］.Acta Electronica Sinica，2000，28(3):69－72.(in Chinese)

［6］ Liang Hong，Ho K C.Identification of digital modulation types using the wavelet transform［C］∥MILCOM 1999.Piscataway:IEEE，1999:427－431.

［7］ 李建勋，秦江敏，马晓岩.Kohonen 网络用于雷达抗速度欺骗干扰中的特征提取［J］.雷达科学与技术，2004，2(2):82－86.LI Jian－xun，QIN Jiang－min，MA Xiao－yan.Feature extraction with Kohonen network against radar velocity－deception jamming［J］.Radar Science and Technology，2004，2(2):82－86.(in Chinese)

［8］ 常宇亮，赵锋，代大海，等.弹道导弹有源干扰的极化抑制［J］.信号处理，2009，25(3):423－429.CHANG Yu－liang，ZHAO Feng，DAI Da－hai，et al.Polarization suppression of active interference in the middle part of missile trajectory［J］.Signal Processing，2009，25(3):423－ 429.(in Chinese)

［9］ 顾冬梅.连续波雷达信号识别与参数提取技术研究［D］.南京:南京信息工程大学，2009.GU Dong－mei.Study on identification and parameter extraction of continuous－wave radar signal［D］.Nanjing:Nanjing University of Information Science and Technology，2009.(in Chinese)

［10］ CHEN Xin－wei，JIN Sheng－cai，QI Shi－shan，et al.An improved correlation method of phase difference detection between two signals in polarimetric radar signal processing system［C］∥2009 Asia Pacific Microwave Conference.Piscataway:IEEE，2009:469－472.

［11］ ZHANG Yin－hao，WU Wen，YANG Guo，et al.DDS－PLL phased source for beam control active phased array［C］∥2008 Asia Pacific Microwave Conference.Piscataway:IEEE，2008:1－4.［12］ WANG Bing－rui，ZHANG Qi－hui，AO Tian－yong，et al.Design of pipelined FFT processor based on FPGA［C］∥ICCMS 2010.Piscataway:IEEE，2010:432－435.

［13］ Cheng Sheng，Tseng Chien－Hsun，Cole Marina.A novel FPGA implementation of a wideband sonar system for target motion estimation［C］∥2008 International Conference on Reconfigurable Computing and FPGAs.Piscataway:IEEE，2008:349－354.

［14］ Naoussi Serge Raoul Dzondé，Berviller Hervé，Blondé Jean Philippe，et al.FPGA implementation of harmonic detection methods using neural networks［C］∥2009 13th European Conference on Power Electronics and Applications.Piscataway:IEEE，2009:1－10.