应急物资储备库多级覆盖选址模型的构建

肖俊华，侯云先

(1.中国农业大学 经济管理学院，北京100083；2.北京劳动保障职业学院，北京102200)

0 引言

应急物资储备库选址问题属于设施选址问题的范畴。设施选址问题是选址问题中传统的一个研究领域，有较长的研究历史，有丰富的研究成果。1963年，Cooper[1]正式提出了设施选址问题，并初步探讨了相关求解方法。Hakimi[2]于1964年发表的论文是设施选址问题发展为一个系统、科学理论的里程碑。此后，选址问题被引入一个更宽广的领域[3-6]。对于应急设施的选址研究，部分文献的选址模型在供应链特征上多为单层覆盖，且服务种类为单源服务，即一个需求点只由距其最近的一个设施点提供服务[7～9]。但考虑到在重大突发事件下，考虑到需求点因对应急物资的需求量巨大而单个设施往往不能满足需求而需要多个设施为其服务的情况，Hogan,K.等[10]提出了一个考虑备用覆盖的最大覆盖模型，该模型在为需求点提供一个服务设施的同时，又提供了一个相同服务质量的备用设施为需求点提供服务。王文峰等[11]对覆盖的概念进行扩展，考虑了应急服务的多源服务特性，提出了一个应急服务设施的多级覆盖选址模型,并运用分布估算法对模型进行求解；葛春景等[12]对重大突发事件应急需求多点同时需求和多次需求的特点，引入最大临界距离和最小临界距离的概念，建立了多重数量和质量覆盖模型，并提出改进的遗传算法进行求解。Murali P等[13]研究了应对生物恐怖袭击时，提出了一个需求不确定的容量限制设施选址模型，该模型中，需求点由多个分布在不同覆盖水平的设施提供服务，运用定位-分配启发式算法进行求解。

本文拟在借鉴上述模型多源服务思想的基础上，对备用覆盖思想进一步延伸，建立应急物资储备库多级最大覆盖选址模型。模型中需求点物资需求由处于不同服务等级的设施点提供，需求点物资的需求量等于各服务等级设施点提供的物资之和；各服务等级由需求点和设施点的距离确定。本文将设计遗传算法，并运用Matlab7.0对模型进行算法实现和算例分析，验证模型和算法的有效性，并以北京市房山区应急物资储备库选址为例进行实证研究。

1 问题描述与模型建立

1.1 问题描述

本文应急物资储备库选址问题涉及两类站点，一类为需求站点，文中统称为需求点；另一类为服务站点，即应急物资储备库，文中统称为设施点。设施点为需求点提供服务，本文以距离表示设施点与需求点之间的联系紧密程度。本文建立应急物资储备库多级最大覆盖选址模型，模型假设如下：

假设1：设施点和需求点均为离散的，且以点状产生；

假设2：任意设施点和需求点的距离可通过调查或计算产生；

假设3：设施点可以建立在需求点上，也可以独立于需求点之外，单独建立；

假设4：设施点可以为多个需求点提供服务，且设施点服务能力无限制；

假设5：待建设施点的数量有限，为p个；

假设6：需求点有k级需求覆盖水平，且在其每一个需求覆盖水平上最多由一个设施为其提供服务，即假设一个需求点有3个需求覆盖水平，则该需求点最多可以有3个设施为其提供服务，如图1所示；

假设7：需求点在k级需求覆盖水平上的需求量为该点需求量的fk倍。

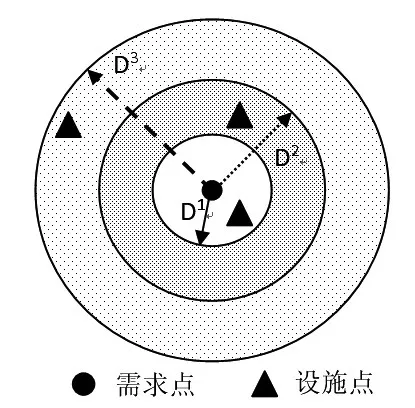
图1 多级覆盖的示意图

1.2 模型的构建

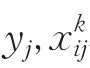
2 模型求解算法设计

最大覆盖选址模型已经被证明为NP-Hard问题[14]，而本文所建多级最大覆盖选址模型是最大覆盖模型的扩展，所以也是NP-Hard问题。遗传算法作为一种实用、高效、鲁棒性强的优化技术，发展极为迅速，已引起国内外学者的高度重视[15]。尽管遗传算法是求解大型组合最优化问题的最具有潜力的方法[16]，并且在许多优化领域都有丰富的文献资料[17]，但是将其应用到设施选址问题尤其是最大覆盖选址问题的研究文献却相对较少[18]。因此，本文利用遗传算法对多级最大覆盖选址模型进行求解，具体实现技术如下：

（1）编码方案

对所有的备选设施按1至n进行赋值，每个代码表示一个基因。每个染色体代表模型的一个可行解，染色体的每一个基因代表选择的备选设施，每一染色体中的基因长度和限定的设施数量相同，假设需选择的设施数为p个，则每个染色体的长度为p。

（2）初始种群的产生

种群的规模和群体的初始化是影响算法收敛性的两个重要因素。Alander[19]的试验结果表明种群规模在染色体长度的一倍到两倍之间是较好的选择，综合考虑种群的多样性要求和计算效率，本文使用染色体长度的2倍，也就是待建设施个数的2倍为种群规模。初始种群中的每个染色体通过随机的方法生成。

（3）适应值计算及评价

染色体的适应度评估由目标函数式（1）来计算。具体计算过程如下：

步骤1：选择第一个需求点，计算其到染色体中每一个基因的距离，对距离进行升序排序，选择前k个距离dk，k∈｛1,2,…,k｝；

步骤2：判断距离dk与各覆盖等级最大距离Dk的关系，若dk小于Dk，则表示需求点可以获得第K级需求覆盖水平的物资量，求出需求点获得的总物资量；

步骤3：重复步骤1-2，遍历全部需求点，得到全部需求点获得的总物资量。

（4）选择、交叉和变异操作

父代的选择采用从群体中随机选择的方式，以保证每个个体都有同样的机会进行交叉；两个父代个体采用传统的单点交叉的方式进行繁殖，生成新的子个体，每对父个体交叉只产生一个子个体。例如：用P1和P2分别表示两个父个体，用C1表示子个体，随机产生交叉点，两个父个体P1：（1 4 6 13 14）和P2：（2 7 8 10 16），设交叉点为3，则生成的子个体为C1：（1 4 8 10 16）；变异操作可以避免算法陷入局部最优解，通常变异率的值较低，本文将变异率设为0.1。

（5）终止条件

遗传算法是一种反复迭代的随机搜索方法，在每次迭代中，记下适应值最大的染色体，直到已经达到了算法规定的最大迭代次数或在规定的连续迭代次数内最好的染色体不再发生变化时算法终止。当算法终止时，最好的染色体即是该选址问题的最优解。

（6）遗传算法具体操作流程

步骤1：对数据进行实数编码，构造备选设施点与需求点之间的距离矩阵Cm×n；定义遗传算法参数（群体规模N、最大遗传代数Maxgen、交叉概率pc、变异概率pm）；

步骤2：用随机的方法生成初始化种群P(0)，令t=1，P(t)=P(0)；

步骤3：计算种群P(t)的适应值；

步骤4：用随机选择策略选择两个父个体P1和P1，进行交叉、变异、重插入等操作得到子种群Q(t)；

步骤5：将P(t)和Q(t)合并，得到新的种群R(t)；

步骤6：对新种群R(t)进行优劣排序，得到P(t+1)；步骤7：t=t+1，判断是否满足结束条件，如果否，转步骤3；否则结束，输出结果(见图 2)。

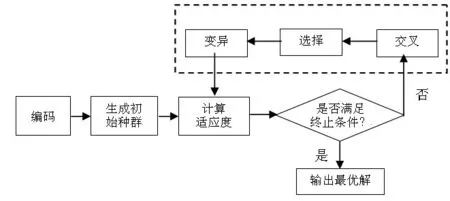
图2 遗传算法流程图

3 算例分析

为验证算法的可行性和分析算法的效果，本文应用Matlab7.0编程，并在DELL N4040笔记本电脑上（双核酷睿i3 CPU，主频2.53G，2G内存）进行了计算实验。假设需求点分别为50、100和200，候选设施点分别为15、20、30，待建设施分别为5、8、10、12。需求点和设施点的位置在一个[0,100]的平面上均匀分布；需求点与设施点的距离为欧式距离。

本文模型为三级水平覆盖，各覆盖等级的覆盖半径由式Dk=δ*max{}dij确定，其中maxdij为需求点和备选设施点的最大距离，m分别为0.2、0.4和0.6；需求点对各覆盖等级的需求百分比分别为60%、30%和10%，为了简化计算，此处假设各需求覆盖水平的权重均为1。表1为各个选址方案的遗传算法运算结果分析。

表1 遗传算法运算结果分析

由表1可知，运用遗传算法分别对50、100和200三种不同规模的需求点的选址方案进行计算，当选择建立12个设施点时，需求点的满意度可达100%，即完全覆盖需求点。实验中各种组合方案的遗传算法运算时间均小于5秒钟，说明遗传算法在求解多级最大覆盖选址模型时具有较好的计算能力。

4 结论

在分析重大突发事件下，传统的最大覆盖选址模型不能满足实际需要的情况下，提出基于备用覆盖和部分覆盖的应急物资储备库的多级覆盖选址模型，考虑了不同覆盖距离提供不同覆盖水平服务的问题。然后基于Matlab7.0设计遗传算法对多级覆盖选址模型进行了求解；并用一个算例验证了模型和算法的可行性和有效性。算例结果显示，本文设计的遗传算法在求解多级覆盖选址模型时具有较高的运算速度和较好的收敛性。

本文在进行应急物资储备库选址时，仅考虑了距离对应急物资储备库选址的影响，且假设设施的服务能力是无限的。在现实中，影响应急物资储备库选址的因素是多方面的，如需求点的灾害风险程度、实际人口密度、设施服务能力等都会对设施选址生影响，同时设施点本身的地质条件、交通条件、建设成本等也会影响设施的选址结果。因此考虑多影响因素，将系统工程理论中多准则决策分析方法和运筹学的组合优化选址模型结合进行应急物资储备库选址将是本文的一个拓展方向。

[1]Cooper L.Location-allocation Problems[J].Operation Research,1963,11.

[2]Hakimi S.L.Optimum Locations of Switching Centers and the Abso⁃lute Centers and Medians of a Graph[J].Operations Research,1964,12(3).

[3]Wang F,Xu Y,Li Y X.A Review of the Discrete Facility Location Problem[J].International Journal of Plant Engineering and Manage⁃ment,2006,11(1).

[4]Brandeau M L,Chui S S.An Overview of Representative Problems in Location Research[J].Management Science,1989,35(6).

[5]Hamacher H W,Nickel S.Classification of Location Models[J].Loca⁃tion Science,1998,6(1).

[6]Klose A,Drexl A.Facility Location Models for Distribution System Design[J].European Journal of Operational Research,2004,162(1).

[7]陆相林,侯云先.基于设施选址理论的中国国家级应急物资储备库配置[J].经济地理,2010,30(7).

[8]陆相林，侯云先，林文，申强.基于设施选址理论的小城镇应急医疗服务中心功能优化——以山东省滕州市为例[J].经济地理,2011,31(7).

[9]陆相林,侯云先,林文,申强.基于选址理论的小城镇应急物资储备库优化配置——以北京房山区为例[J].地理研究,2011,30(6).

[10]Hogan K,C.S.ReVelle.Concepts and Applications of Backup Cover⁃age[J].Management Science,1986,32(22).

[11]王文峰,郭波,刘新亮.多级覆盖设施选址问题建模及求解方法研究[J].中国管理科学,2007,15(z1).

[12]葛春景,王霞,关贤军.重大突发事件应急设施多重覆盖选址模型及算法[J].运筹与管理，2011,20(5).

[13]Murali P,et al.Facility Location under Demand Uncertainty：Re⁃sponse to a Large-scale Bio-terror Attack[J].Socio-Economic Plan⁃ning Sciences,2012,46(1).

[14]Kariv O,Hakimi S.An Agorithm Aproach to Ntwork Location Prob⁃lem[J].SIAM Journal of Applied Mathematics,1979,37.

[15]雷英杰,善文等.MATLAB遗传算法工具箱及应用[M].西安：西安电子科技大学出版社,2005.

[16]王小平,曹立明.遗传算法——理论、应用与软件实现[M].西安：西安交通大学出版社,2003.

[17]赵冬玲,孔志周,官东.基于改进遗传算法的物流配送中心选址研究[J].统计与决策,2008,(11).

[18]Jorge H J,Joy B,Rajan B.On the Use of Genetic Algorithms to Solve Location Problems[J].Computers&Operations Research,2002,29.

[19]Alander J T.On Optimal Population Size of Genetic Algorithms.Pro⁃ceedings of CompEuro,1992.