一种新的Malmquist指数测算与分解方法

鲁 涛，陆邦祥

（南京理工大学经济管理学院，南京210094）

0 引言

Malmquist生产力变化指数是由Caves等（1982）在Malmquist(1953)文献的激发下引入的。Malmquist指数度量生产力变化，并通过分解为前沿面移动和效率变化因素，包含着有关生产力变化的来源信息。Fare等（1994a）定义了可用距离函数，例如DEA分数来计算的Malmquist指数。另一个可用DEA分数计算的Malmquist指数的基期形式，则由Berg等（1992）引入。Malmquist指数的分解，尤其是Fare等的定义（其常被称为相邻Malmquist指数）在各种文献中引起了相当关注。但是，本文却是探讨Malmquist指数的另一方面——合成而不是分解。

前沿面移动或技术变化可以被认为是一个全局现象，它常由改变的经济条件、改善的技术条件这些因素的出现而带来。很多情况下，这些因素对于分析中的观察值，也即DMU（它们之间假定是可以比较的），可被假定为一致或大体相似的，因此某一值就可被用来代表所有DMU的前沿面移动。传统做法中，Malmquist指数和其分解都是个体或局部计算，而整体描述的，即从个体角度计算的前沿面移动利用加权或不加权的几何平均数（有时为算术平均数）来加和。因此，总体的结论就基于这些平均值做出，例如“前沿面在研究的时期内向外移动10%”即为此类典型表述。

本文将提出一个测算全局指数的新方法，它在就某一个全体视为整体（而不是单独的观察值）的生产力变化，尤其是前沿面移动做出判断时很有用。本文将定义相邻与基期Malmquist指数的全局形式，同时也包括相应的前沿面移动的全局形式。本文还要表明，与传统的大多数典型的利用（不加权）几何平均数对个体指数加和的方法相比，全局指数的测算具有的优势。

1 基于DEA的Malmquist指数

1.1 相邻Malmquist指数

1.2 基期Malmquist指数

以时期t0的参考技术作为基期参考技术的基期Malmquist指数给定如下：

2 全局Malmquist指数及其基本性质

相邻指数（4）中的前沿面移动特定于待评价的观察值，它是从时间t和t+1对应的DMU所观察到的前沿面移动的几何平均数。然而，技术变化常被认定为是一个全局，而非局部现象。该点在很多实证应用中表现明显，个体或局部前沿面移动的平均值会被作为总体的技术变化来报告和描述。下面，将给相邻和基期指数定义一个测算全局指数的不同方法。

2.1 全局相邻指数与前沿面指数

式(9)与Balk和Althin（1996）的多边技术变化指数类似。

值得注意的是，全局前沿面移动的计算非常简单：（1）计算所有K×T个DMU相对于每一时间阶段的距离；（2）对于T个前沿面中的每一个，计算K个距离的几何平均值;（3）计算每对时间阶段的比率。

鉴于全局前沿面移动可理解为相对于已有前沿面的平均移动，它也表现出Hicks中性移动，而与此值不同的局部指数表现出非Hicks中性移动。因此，它可以作为相邻指数的一种替代分解形式。

它是样本中K个观测值在t和t+1之间各自效率变化的几何平均值。因此，我们可以定义相邻生产力变化的全局指数为：

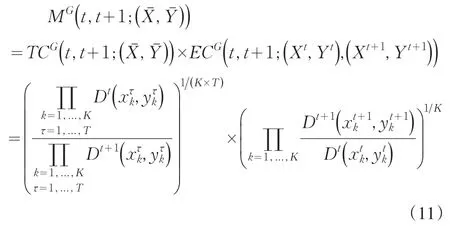
2.2 全局基期Malmquist与前沿面移动指数

上述指数是基于相邻生产力变化指数来构建的。如果偏好基期指数，也可以基于其给出一个消除了基期选择任意性的全局指数形式，全局前沿面移动可定义为：

它是样本中每一DMU利用每一时期基于基期所得前沿面移动的几何平均值。基于基期，现在可定义t和t+1之间的生产力变化指数如下：

如果t=2，则全局相邻指数（11）、（10）和（9）则变为传统相邻指数的几何平均值（2）、（3）和（4），与此相似，（13）、（10）和（12）则变为与（5）、（6）和（7）的平均值相同。但是当时间阶段大于2时，全局指数将给出对真实前沿面移动的较好测算，并也具有传递性的优势。

2.3 全局指数性质

式（8）所定义的时期t的技术指数是数据集中所有观测值（所有时间阶段所有DMU）相对时期t的前沿面距离的几何平均值。时期t和t+1之间全局前沿面移动则用两个阶段的技术指数比率来计算。该方法的结果则是，每个前沿面上的K×T个点被用来计算前沿面之间的距离。使用传统的合成平均值方法，每一前沿面上只有2×K个点被用来计算相邻指数（对于基期指数，则只有K个点被使用）。因此，全局指数就给出了一个真实前沿面移动的较好测算，特别是对较为稀疏的总体数据集来说更是如此。后面的有关讨论和例子将局限于相邻指数的全局形式，但是相应的结论对于基期指数的全局形式也是类似的。

为了探求全局相邻指数（11）和全局基期指数（13）的不言自明的性质，使用了Altin（2001）的测试方式来进行评价。对于传统的相邻、基期指数（2）和（5）同相应的全局指数的评价结果概括于表1中，全局指数的相应证明限于篇幅不再给出。鉴于全局指数涉及整个数据集而不是单个的观测值，相应的测试根据这些指数进行了修改。

表1 不同指数的指数测试

全局相邻指数同局部指数相比，满足传递性的特征。同时，全局基期指数则独立于基期的选择，因为T个时期中每一个作为基期的平均值都得到了使用，从而消除了基期选择的任意性。但是，全局指数的一个缺陷在于，因为样本中的所有观测值都（源于所有时期）都参与了计算，因此。它对于在数据集中增加额外的数据（DMU或是时间周期）敏感。

3 实证研究

本文首先利用中国道路交通运输业相关数据，计算其全局相邻生产力变化指数、全局相邻前沿面移动指数和全局相邻效率变化指数。而后，利用全局指数去计算中国道路交通运输业六大区域的前沿面差异。

3.1 决策单元的选择、处理及分组

DEA方法的核心概念是决策单元。使用基于DEA的Malmquist指数方法的一个重要前提是：决策单元数不能太少，至少是模型变量数的两倍。而本研究中所涉及的决策单元有31个，即全国各省、自治区和直辖市的道路交通运输部门。

在计算中国道路交通运输业各区域前沿面差异时，划分为六大区域，即华北区，包含北京、天津、河北、山西、内蒙古；东北区，包含辽宁、吉林、黑龙江；华东区，包含上海、江苏、浙江、安徽、福建、江西、山东；中南区，包含河南、湖北、湖南、广东、广西、海南；西南区，包含重庆、四川、贵州、云南、西藏；西北区，包含陕西、甘肃、青海、宁夏、新疆。

3.2 输入输出指标构建

应用DEA技术，首先需要界定研究对象的投入指标和产出指标。以下对本研究产出和投入指标的选择及数据来源和处理情况进行说明。

（1）产出指标。比较合理的选择是将“道路运输行业附加值”作为产出指标，但是该指标尚无法获得。目前交通行业常用运输周转量这一指标反映各种运输方式提供服务的数量。因此从指标数据可得性的角度，分别以道路客运周转量和道路货运周转量等实物量指标作为道路交通运输业的产出指标。

（2）投入指标。就投入而言，可选用的指标较多，例如资本存量、运输线路长度、运输工具数、从业人员数和能源消耗量等指标均可作为投入指标。从基本的投入看，一个是资本，一个是劳动。

就资本投入而言，最理想的是服务流量，但是其难以直接度量。劳动投入量包括就业人数、劳动时间、劳动强度和劳动质量等方面的内容。但考虑到指标在交通各部门间的可比性及可累加性，以及指标数据可获得性，本研究选取了二项指标作为投入指标：公路里程和年底职工人数。

3.3 模型求解结果及分析

3.3.1 中国道路交通运输业全局相邻生产力变化指数、前沿面移动指数及效率变化指数

根据上面确定的各项指标及数据,可以求出1998～2007年我国道路运输业的全局Malmquist相邻生产力变化指数、前沿面移动指数及效率变化指数。为了便于比较，也给出了基于效率变化与技术进步的传统Malmquist指数及其分解，表2中数据根据《中国统计年鉴》(1999～2008年)计算得到。为直观反映表2，将其数据反映到图1中。

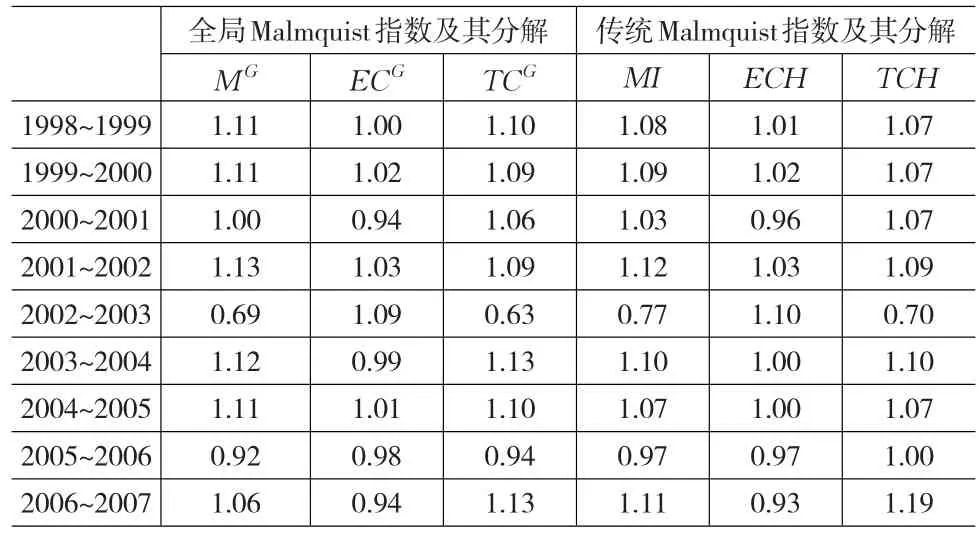
表2 全局Malmquist指数及其分解与传统Malmquist指数及其分解

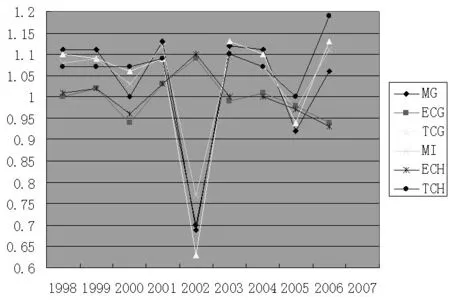
图1 全局Malmquist指数及其分解与传统Malmquist指数及其分解

按照本文的研究方法，全局Malmquist相邻生产力变化指数可以分解为两个部分，即相邻前沿面移动指数和相邻效率变化指数。而传统的生产力指数MI则被分解为两个部分，即效率变化指数ECH，技术变化指数TCH。由图可知，除了2002～2003年和2005～2006年间全局Malmquist指数MG小于1，表示生产力水平下降（2002～2003下降幅度尤其巨大）外，其他年份间的生产力水平均是增长的。而全局效率变化指数ECG除了2000～2001年、2003～2004年、2005～2006年、2006～2007年小于1，表明技术效率下降外，其他年份不变或增加，但是波动幅度不大。而全局前沿面移动指数TCG除了2002～2003年和2005～2006年间小于1，表明技术变化下降（其中2002年到2003年下降犹大）外，其他年份间的技术变化都是提升的。全局前沿面移动指数TCG的走势同全局Malmquist指数MG的变化趋势基本相同，这反映了生产力的变化基本上可以由技术的变化来解释。与传统Malmquist指数及其分解相比，MG指数的变化趋势同MI指数基本相同，但是波动幅度相对较大些，生产力水平提升和下降的年份区间也比较吻合。ECG指数同ECH指数则几乎重合，反映了几乎相同的技术效率变化趋势和变化程度。TCG指数同TCH指数则反映了技术变化的相似趋势，两者的波动幅度也比较接近。

3.3.2 中国道路交通运输业六大区域前沿面差异

当数据点属于不同群组的观察点而不是不同时间段的观察点时，我们仍然可以利用上述的全局指数去计算全局前沿面移动或者前沿面之间的差距。例如当我们要去比较各省、自治区和直辖市的道路交通运输业状况时，用全局指数计算的其前沿面差距就可提供丰富信息。

对于T群组中的每一群组，假设K()t是群组t中所含DMU的数目（本文中指中国各省、自治区和直辖市的道路交通运输业），而KT是DMU的总数，即

而前沿面间的差距可以由式（9）给出。

表3 中国道路交通运输业分区域前沿面差距度量

表2反映了中国交通运输业六大区域的前沿面差距，它在一定程度上反映了这些区域整体技术方面的差异，例如华北地区与华东地区之间的前沿面距离是1.67。则从技术角度讲，则华东地区平均优于华北地区67%。

4 结语

传统做法中，Malmquist指数及其分解都是个体或局部计算，整体描述的，即从个体角度计算的Malmquist指数、技术效率及前沿面移动利用加权或不加权的几何平均数（有时为算术平均数）来加和，因此总体的结论就基于这些平均值做出。本文首先提出一个测算全局指数的新方法，通过提出全局Malmquist指数来测量将某一全体视为整体（而不是单独的观察值）的生产力变化，并将其分解为全局技术效率变化和全局前沿面移动。与传统指数及其分解相比，全局指数具有一些独特优点。其次，利用该方法对1998年到2007年的中国道路运输业进行了实证研究，测算了全局相邻Malmquist指数、全局相邻技术效率变化及全局前沿面移动，并将其同传统Malmquist指数及其分解进行了比较，得出了相似的结论。而且，还利用该指数方法测量了中国六大区域的道路交通运输业前沿面之间的距离，反映了其在平均技术水平上的相对差异。

[1]D.Althin.Measurement of Productivity Changes：Two Malmquist Index Approaches[J].Prod.Anal.2001,(16).

[2]B.M,Balk, Scale Efficiency and Productivity Change[J].Prod.Anal.2001,(15).

[3]R.Fare,E.Grifell-Tatje,S.Grosskopf,C.A.K Lovell.Biasd Technical Change and the Malquist Productivity Index[J].Scan.J.Econ.,1997,(99).

[4]R.fare,S.Grosskopf,B.Lingdgren,P.Roots,Productivity Changes in Swedish Pharmacies1980-1989：A Nonparametric Malmquist Ap⁃proach[J].Journal of Productivity Analysis,1992,(3).

[5]R.fare,S.Grosskopf,M.Norris,Productivity Growth,Technical Prog⁃ress and Efficiency Changes in Industrialized Countries[J].American Economic Review,1994,(84).

[6]R.fare,S.Grosskopf,M.Norris,Productivity Growth,Technical Prog⁃ress and Efficiency Changes in Industrialized Countries：Reply[J].American Economic Review,1997,(87).

[7]T.Oum,M.Tretheway,W.WatersⅡ,Concepts,Methods and Purpose of Productivity Measurement in Transportation[J].Transportation Re⁃search Part A：Policy and Practice,1992,(26).

[8]余思勤,蒋迪娜,卢剑超.我国交通运输业全要素生产率变动分析[J].同济大学学报（自然科学版）,2004,(6).

[9]张越,胡华清.基于Malmquist指数的中国航空公司全要素生产率分析[J].北京理工大学学报（社会科学版）,2007,(12).

[10]于剑.基于Malmquist指数的中国航空公司全要素生产率分析[J].北京理工大学学报（社会科学版）,2007,(12).

[11]刘玉海,林建兵,翁嘉辉.中国道路运输业营运效率动态分析——基于Malmquist生产力指数[J].产业经济研究,2008,(1).

[12]王亚华,吴凡,王争.交通行业生产率变动的Bootstrap-Malmquist指数分析（1980～2005）[J].经济学（季刊）,2008,(3).

[13]田刚,李南.中国物流业技术进步与技术效率研究[J].数量经济技术经济研究,2009,(2).