低渗透双重介质油藏试井解释模型
2012-02-19张艳玉李卫东崔国亮李素芹
张艳玉, 李卫东, 崔国亮, 李素芹
(中国石油大学(华东) 石油工程学院,山东 青岛 266555)
0 引言
天然裂缝性油藏分布广泛,为油气的主要储层.由于其具有明显的双重介质特征,所以可以用双重介质模型来描述裂缝性油藏的渗流特征[1-5].低渗透油藏中原油流动不满足达西定律,并且大量实验证明,低渗透油藏渗透率随净压力的增加呈指数递减规律,所以引入渗透率模数来计算渗透率.基于上述特征,综合考虑井筒储存和表皮系数建立了低渗透双重介质油藏试井解释模型[6-11],并采用数值方法进行求解[12],绘制了压力和压力导数曲线,并进行参数敏感性分析.
1 模型的建立和求解
1.1 物理模型
低渗透双重介质油藏由裂缝和基岩两种连续介质组成,流体通过裂缝系统和基岩系统同时流向井筒,同时,基岩系统向裂缝系统发生拟稳态窜流.考虑如下假设条件:
(1)低渗透双重介质油藏中一口井以定产量生产;
(2)油井生产前,地层压力分布均匀,基岩和裂缝具有相同的初始压力;
(3)流体单相弱可压缩,在地层中的流动为等温流动,流体流动满足低速非达西定律,具有启动压力梯度;
(4)考虑井筒储存和表皮系数的影响,忽略重力和毛管力的影响;
(5)每种介质的孔隙度与另外一种介质的压力变动相独立.
1.2 数学模型
符合低渗情况的非达西运动方程为:
(1)
式中:vr为渗流速度,m/s;Kr是低渗透介质的渗透率,μm2;μ为流体的粘度,mPa·s;Gr为启动压力梯度,MPa/m.

由运动方程、状态方程和连续性方程,得到低渗透双重介质油藏无因次试井解释数学模型如下:
初始条件:Pfd(rD,TD=0)=PmD(rD,TD=0)=0
内边界条件:
外边界条件:PfD(∞,TD)=PmD(∞,TD)=0
式中:PfD、PmD分别为裂缝和基质的无因次压力;PwD为无因次井筒压力;GfD、GmD分别为裂缝和基质的启动压力梯度;λmf为基质和裂缝之间的窜流系数;Sf、Sm为裂缝和基质的表皮系数;ωf为弹性储容比;γfD、γmD为裂缝和基质的渗透率模数;CD为无因次井筒储存系数;rD为无因次半径;TD=tD/CD为无因次时间;Kfr=Kf/(Kf+Km),Kmr=Km/(Kf+Km)为渗透率比.
1.3 模型求解
在时间方向上,为精确反映早期段井筒储存效应的影响,采用指数递增时间,取
Tn=0.01×100.025(n-1)
模型中的偏微分方程为二阶非线性方程,难以求出解析解,只能采用数值方法求解[12].对偏微分方程组进行全隐式差分离散,在空间方向上,对第m个点采用向前差商;在时间方向上,对第n个点采用向后差商,二阶导数采用二阶中心差商.采用Broyden秩1方法求解偏微分方程组的解,工作量较小,程序运行速度较快.
2 典型曲线特征和参数敏感性分析
2.1 典型曲线特征
低渗透双重介质油藏的压力特征分为3个阶段:早期径向流、基岩向裂缝的窜流阶段,晚期径向流.由于受到低速非达西效应和油藏应力敏感性的影响,在压力导数和时间的双对数图上,曲线不会出现0.5水平直线段,而是呈现为上翘的曲线.
纯井筒储存阶段结束后,启动压力梯度和渗透率模数均会使曲线出现上翘,油藏压力下降速度加快,但启动压力梯度的影响远远大于渗透率模数的影响.渗透率模数使得曲线在渗透率模数为0的曲线基础上近似平行上移,“凹子”的大小不变,而启动压力梯度不仅会使“凹子”上移,而且会使得“凹子”变浅.
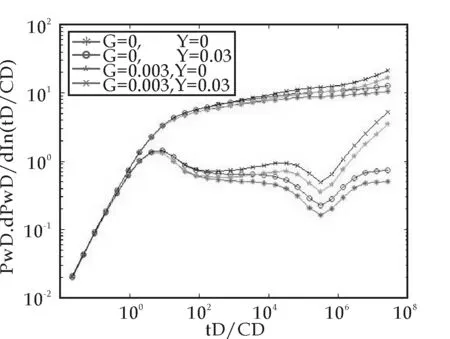
图1 典型压力和压力导数双对数图
2.2 渗透率比的影响
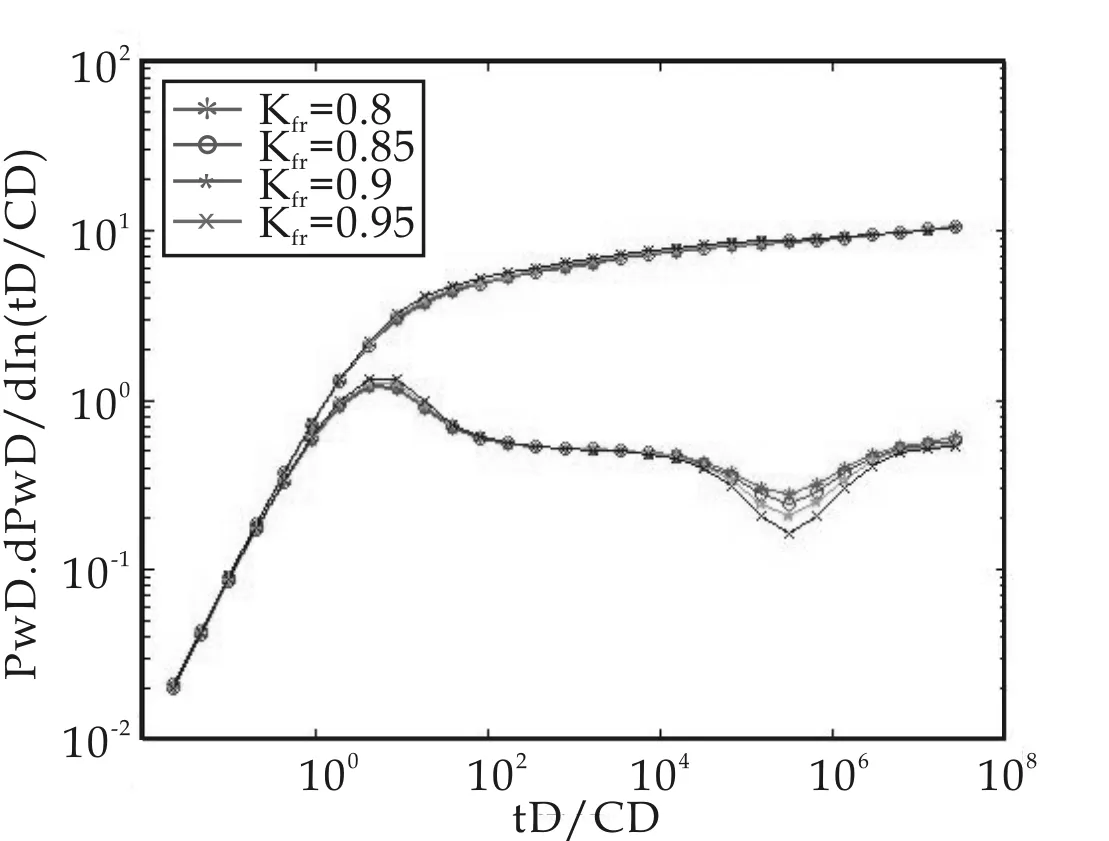
图2 只考虑基岩启动压力梯度时渗透率比的影响
图2是只考虑基岩启动压力梯度,其他参数不变,渗透率比变化时的压力和压力导数双对数图.从图中可以看出,随着渗透率比的增大,曲线的中后期有所上翘,但上翘的幅度不大,后期偏离0.5水平线的幅度也不大.
图3是只考虑裂缝启动压力梯度,其他参数不变,渗透率比变化时的压力和压力导数双对数图.从图中可以看出,随着渗透率比的增大,后期压力和压力导数曲线明显上翘,上翘幅度比只考虑基岩启动压力梯度时的大.
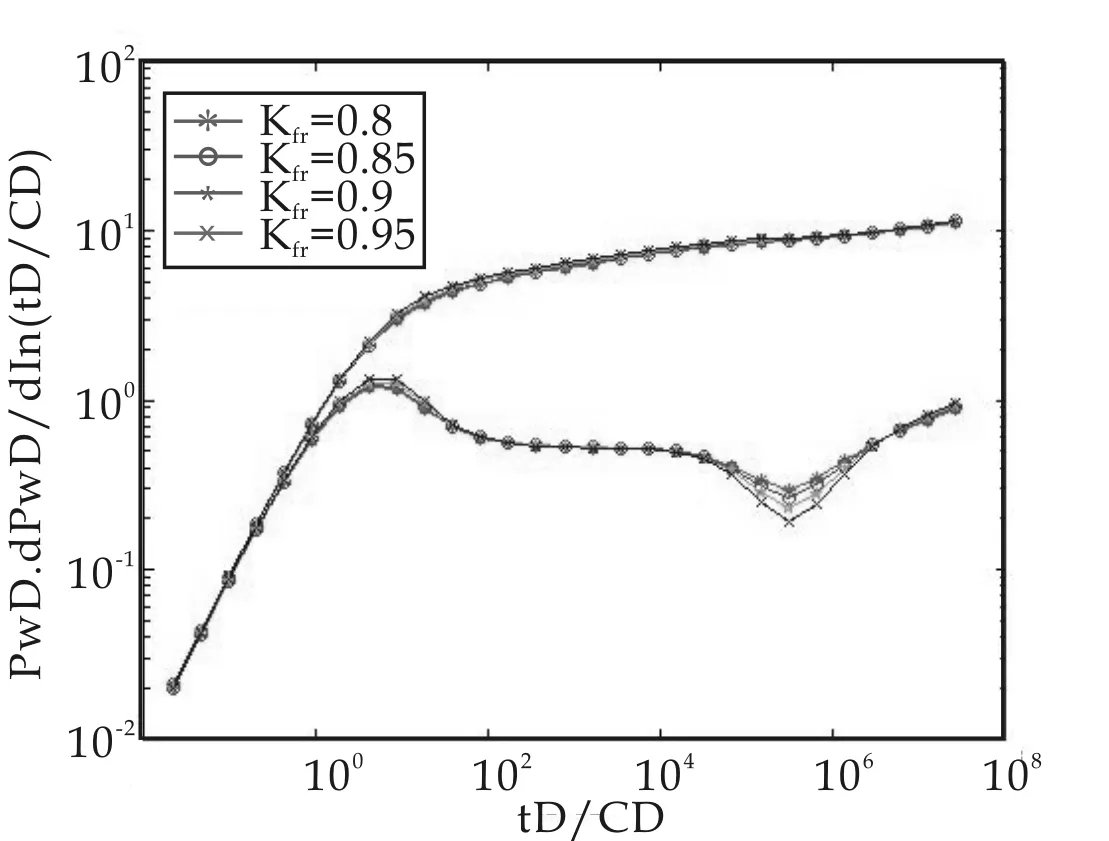
图3 只考虑裂缝启动压力梯度时渗透率比的影响
2.3 启动压力梯度的影响
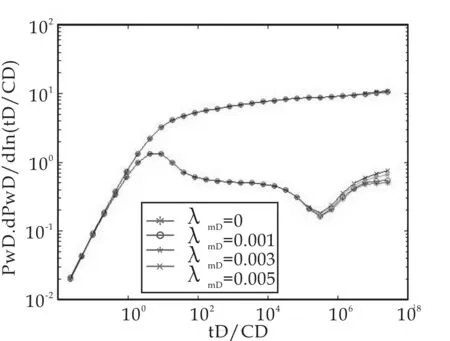
图4 只考虑基岩启动压力梯度的影响
图4是只考虑基岩启动压力梯度变化时的压力和压力导数曲线图.从图中可以看出,随着基岩启动压力梯度的增大,压力和压力导数曲线在后期出现上翘,但是上翘的幅度并不大.
图5是只考虑裂缝启动压力梯度变化时的压力和压力导数曲线图.从图中可以看出,随着裂缝启动压力梯度的增大,压力和压力导数曲线在中后期出现明显上翘,并且启动压力梯度越大,上翘的幅度越大,上翘也越早.
图6是同时考虑基岩和裂缝启动压力梯度变化时的压力和压力导数曲线图.从图中可以看出,当基岩和裂缝启动压力梯度的增大幅度相同时,曲线的形状和图5非常相近.

图5 只考虑裂缝启动压力梯度的影响
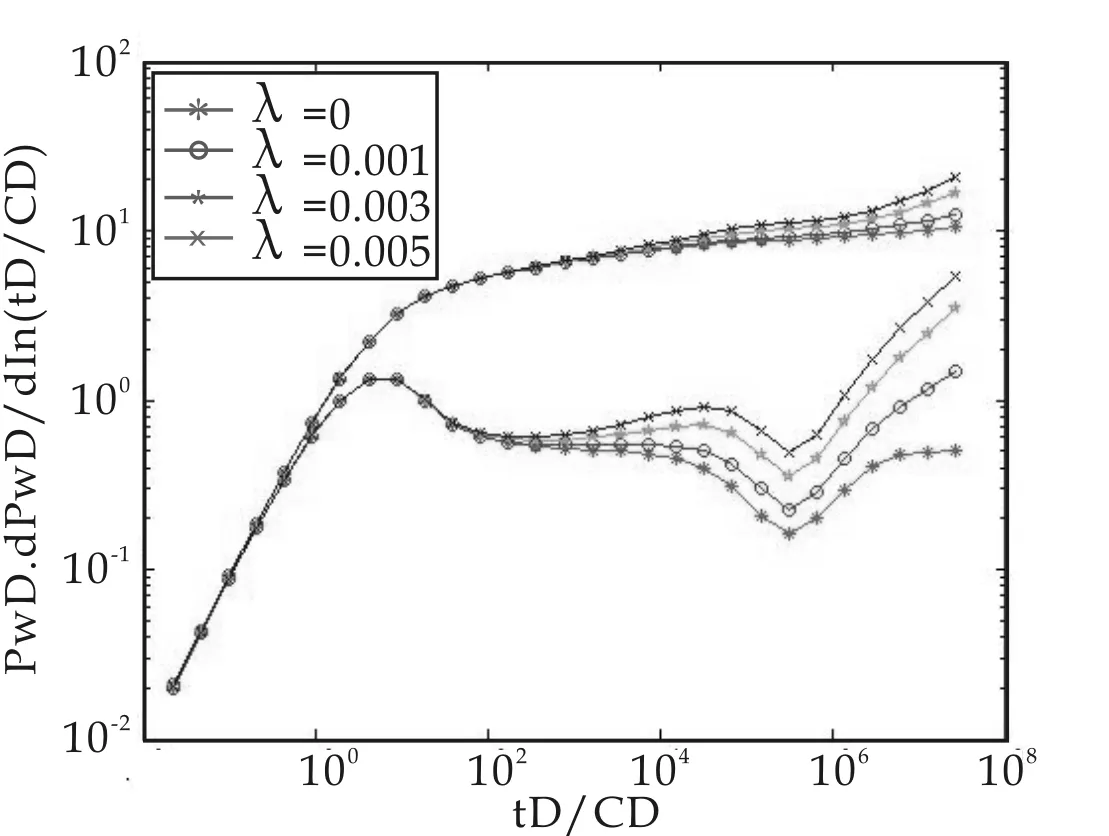
图6 同时考虑基岩和裂缝启动压力梯度的影响
2.4 渗透率模数的影响
图7是不考虑基岩和裂缝的启动压力梯度的情况下,只考虑基岩渗透率模数变化的压力和压力导数曲线图.从图中可以看出,随着基岩渗透率模数的增大,压力和压力导数曲线的变化非常不明显.
图8是不考虑基岩和裂缝的启动压力梯度的情况下,只考虑裂缝渗透率模数变化的压力和压力导数曲线图.从图中可以看出,随着裂缝渗透率模数的增大,压力和压力导数曲线在中后期出现明显上翘,并且裂缝渗透率模数越大,上翘程度越大,压降速度增加.
图9是不考虑基岩和裂缝的启动压力梯度的情况下,同时考虑基岩和裂缝渗透率模数变化时的压力和压力导数曲线图.从图中可以看出,当基岩和裂缝启动压力梯度的增大幅度相同时,曲线的形状和图8非常相近.
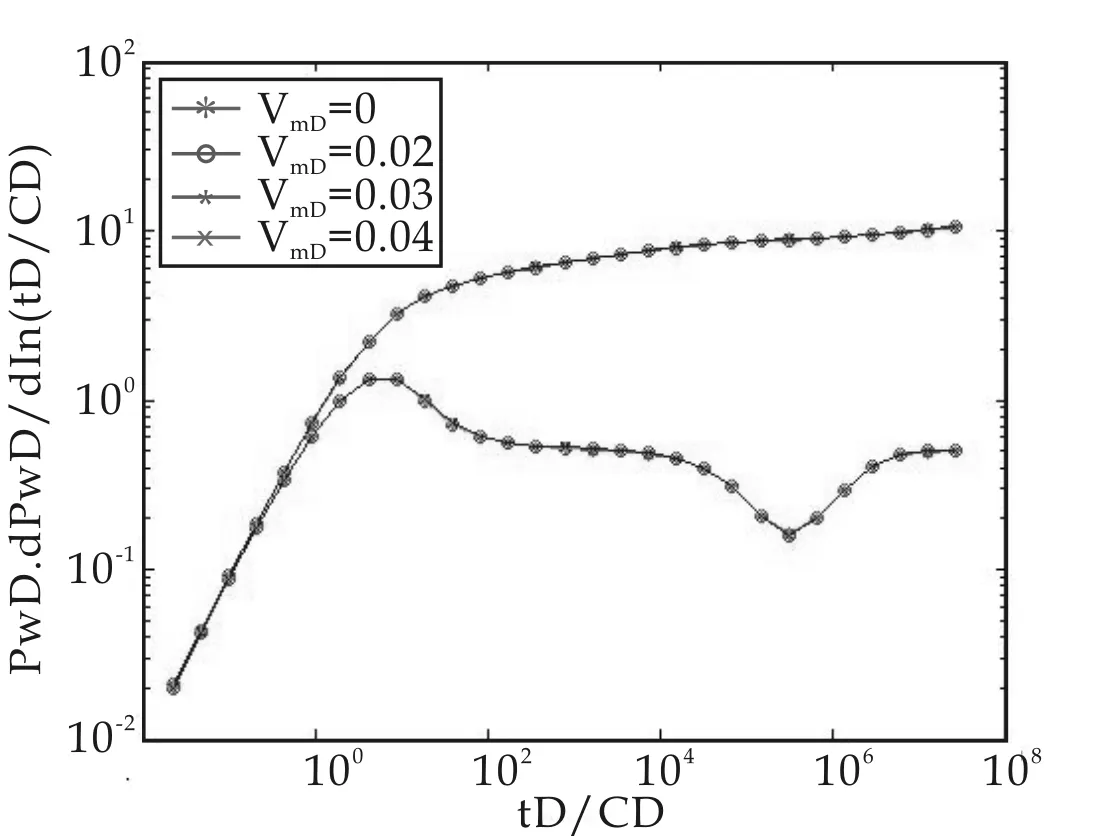
图7 只考虑基岩渗透率模数的影响

图8 只考虑裂缝渗透率模数的影响

图9 同时考虑基岩和裂缝渗透率模数的影响
通过以上8幅图(图2~9)的变化可以看出,在双重介质油藏试井模型情况下,由于裂缝系统的渗透率占很大的比重,因而对后期压力响应的影响起主要作用的是裂缝系统启动压力梯度和渗透率模数的影响,而基岩系统启动压力梯度和渗透率模数的变化对压力响应并不是特别敏感.
2.5 表皮系数的影响
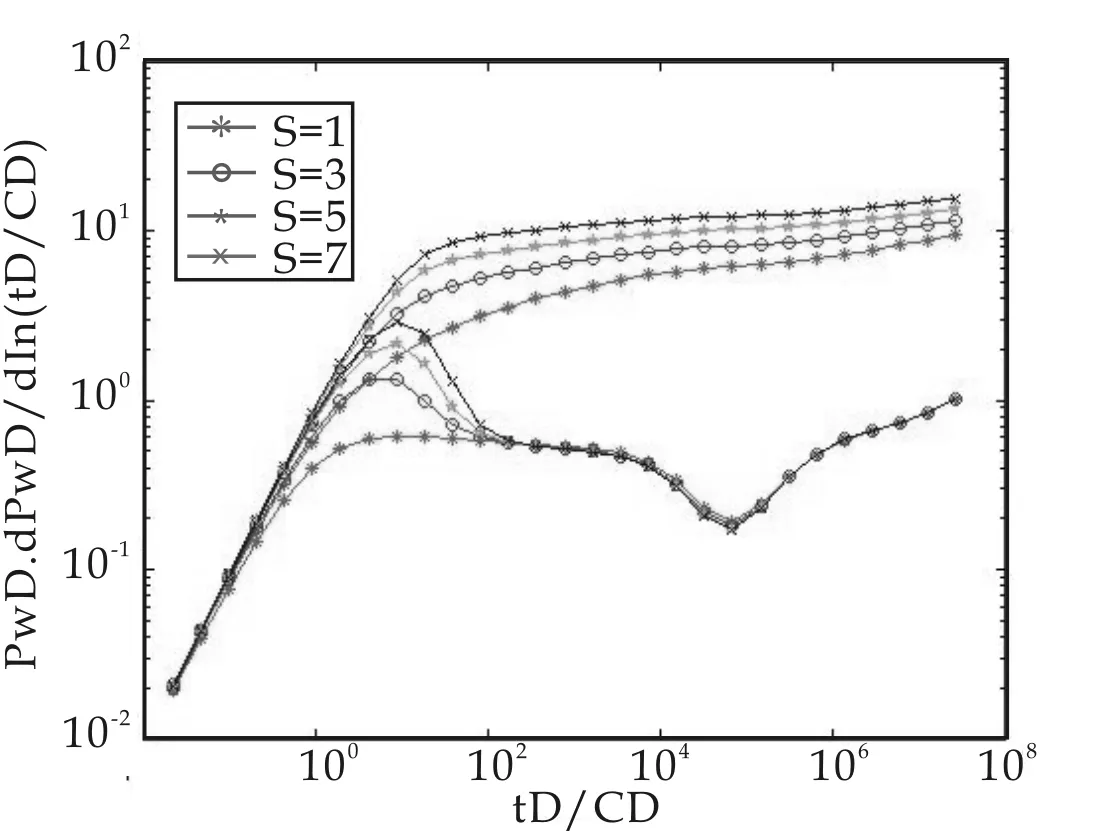
图10 表皮系数影响的压力和压力导数双对数图
从图10中可以看出:表皮系数影响压力导数曲线“驼峰”的高低,表皮系数越大,峰值越高,井污染越严重.在曲线中后期,压力导数曲线互相重合,井底压力下降速度相同.
2.6 井筒储存系数的影响

图11 井筒储存系数的影响
在基岩向裂缝的窜流段,存在两种不同的情况:当无因次井筒储存系数较小时(图11中为CD<1),其影响持续不到基岩向裂缝的窜流期时,不会影响压力导数曲线“凹子”的大小,但是随着CD的增加,“凹子”平行左移;但当CD取值较大(CD>1)时,会影响压力导数曲线“凹子”的宽度和深度,且CD越大,“凹子”越浅,当CD≥3000时,“凹子”消失,压力和压力导数曲线呈现出均质低渗透油藏试井曲线特征.
2.7 弹性储能比的影响
弹性储能比越小,“凹子”的宽度和深度越大,窜流过渡持续的时间越长;ω越大,与此相反.ω越接近于1,低渗透双重孔隙介质油藏的压力动态特征越接近于均质地渗透油藏的压力动态特征.在图中,当ω=0.95时,压力导数曲线的“凹子”消失,呈现均质低渗透油藏试井曲线特征.在后期,所有压力和压力导数曲线重合在一起,井底压降速度相同.

图12 弹性储能比的影响
2.8 窜流系数的影响
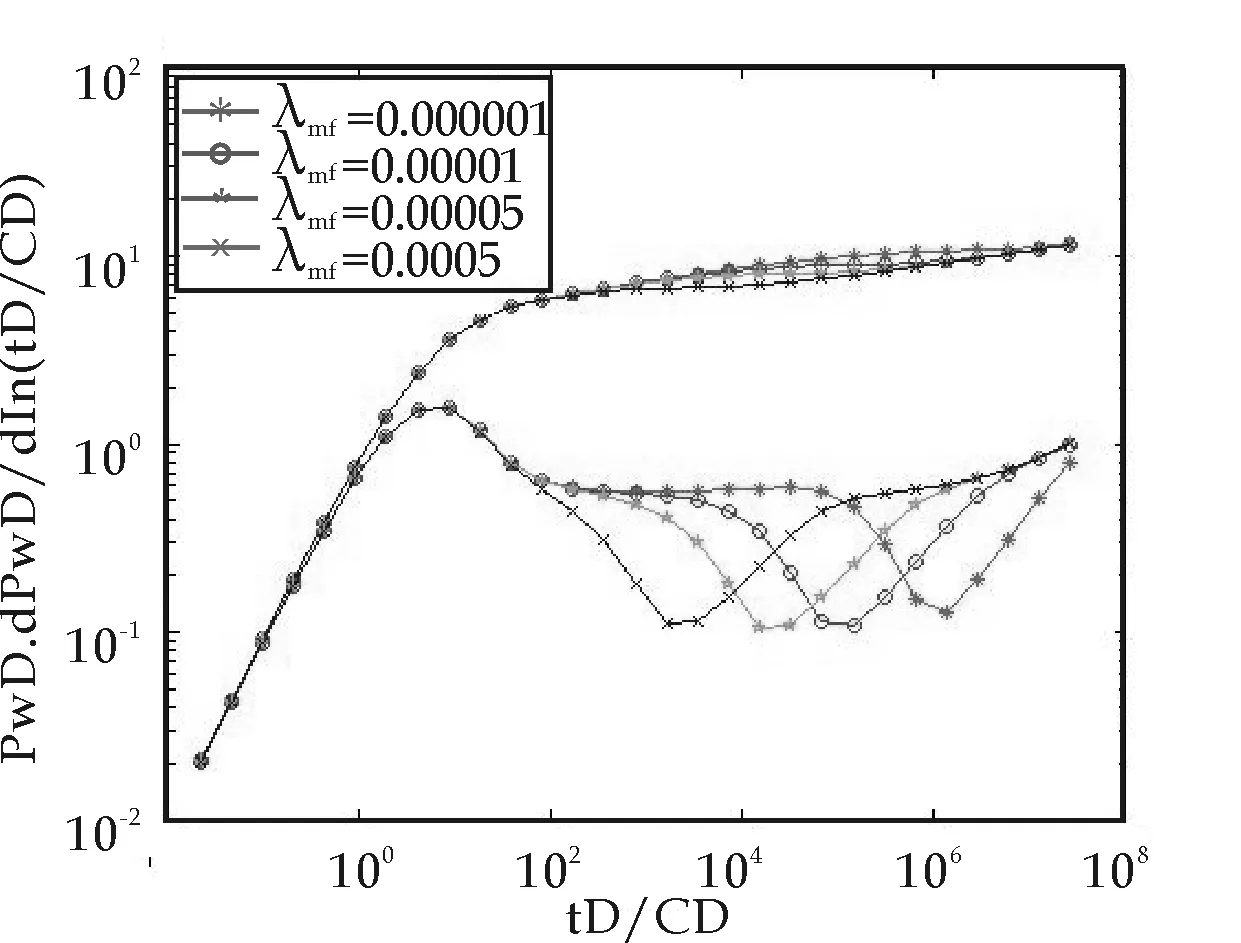
图13 窜流系数的影响
在压力导数曲线上,窜流系数决定过渡段“凹子”的位置,随着窜流系数的增加,“凹子”向左下方移动,过渡段的时间提前,“凹子”的形状、大小不变.当窜流系数大到一定程度(图中为0.0005),则井筒储存效应结束之后,直接到达基岩向裂缝的窜流阶段.在流动后期,所有的压力和压力导数曲线均重合到一起,井底压力下降幅度和速度相同.
3 结束语
(1)启动压力梯度和渗透率模数均会使双重介质油藏中后期的压力和压力导数曲线出现上翘.渗透率模数使曲线在渗透率模数为0的基础上出现上移,“凹子”的大小不变;而启动压力梯度使曲线上翘的程度远大于渗透率模数使曲线上翘的程度,且会影响“凹子”的大小和位置.
(2)在双重介质油藏试井模型情况下,由于裂缝系统的渗透率占很大的比重,因而对后期压力响应的影响起主要作用的是裂缝系统的启动压力梯度和渗透率模数,而基岩系统的启动压力梯度和渗透率模数的变化对压力响应并不是特别敏感.
(3)表皮系数影响压力导数曲线“驼峰”的高低,表皮系数越大,峰值越高,井污染越严重;随着井筒储存系数的增加,“凹子”平行左移.
(4)弹性储能比越小,“凹子”的宽度和深度越大,窜流过渡持续的时间越长;窜流系数越大,过渡段出现的时间越早.
[1] 闫庆来,何秋轩. 低渗透储层中油水渗流规律的研究[M].低渗透油气藏开发技术.北京:石油工业出版社,1993.
[2] 尹洪军,何应付. 变形介质油藏渗流规律和压力特征分析[J]. 水动力学进展与研究[A 辑],2002,17(5):538-546.
[3] 同登科,张海英. 变形介双重质分形油藏渗流流动分析[J].石油大学学报(自然科学版),2003,27(4):76-79.
[4] 同登科,刘敏鸽. 双重介质分形油藏线性流动分析[J].石油大学学报(自然科学版),2003,27(2):59-62.
[5] 同登科,姜东梅,陈钦雷. 变形双重介质油藏动态特征[J]. 石油大学学报(自然科学版),2001, 25(5):53-56.
[6] 程时清,李跃刚. 低速非达西渗流试井模型的数值解及其应用[J].天然气工业,1995,16(3):27-30.
[7] 程时清,李功权. 双重介质油气藏低速非达西渗流试井有效井径数学模型及典型曲线[J].天然气工业,1997,17(2):35-37.
[8] 何国良,向开理. 变形介双重质分形油藏渗流渗流数学模型[J].西南石油学院学报,2002, 24(4):24-27.
[9] 同登科,姜东梅,陈钦雷. 变形双重介质油藏开发特征[J]. 应用力学学报,2002, 19(2):56-60.
[10] 宋付权,刘慈群. 变形介质油藏试井分析方法[J].油气井测试,1998.
[11] 曹绪龙,同登科,王瑞和. 考虑二次梯度项影响的非线性不稳定渗流问题的精确解[J].应用力学和数学,2004,25(1):93-99.
[12] 陆金甫,关 治.偏微分方程数值解法[M]. 北京:清华大学出版社,1987.
