型材滚弯数值模拟及应力、应变分析
2012-02-19陈高翔王亚锋
陈高翔, 王亚锋
(西安西电高压开关有限责任公司, 陕西 西安 710018)
0 引言
型材弯曲件在汽车、家用电器、船舶、建材等民用领域、导弹及其发射架制造、飞行器制造等军用领域的应用日益广泛.飞机制造中滚弯工艺主要用于成形框肋缘条,机身前后段和发动机短舱的长桁,这些都是组成飞机骨架的受力零件.滚弯加工过程十分复杂,它涉及到几何非线性、材料非线性和接触非线性的多重非线性问题,成型规律不易把握[1-4].
由于滚弯成形过程影响因素很多,传统的物理实验法成本高、周期长,而且存在着各种误差.近年来,有限元分析被认为是对型材弯曲回弹预测的最有效的方法[5,6].本文将运用显式动力学有限元分析软件ANSYS/LS-DYNA对型材滚弯过程进行模拟[5,6],并分析Z型型材滚弯过程腹板中性层的变化,以及成形与回弹过程型材腹板切向应力、应变分布.
1 滚弯成形过程显式有限元模拟
本文模拟数控四轴型材滚弯机的二维成形过程,型材所用材料为7075-O,滚轮材料为45钢.在ANSYS/LS-DYNA中建立的有限元模型[7]如图1所示.型材在上下滚轮的夹持和传导作用下(靠摩擦力进给)向Z轴正向移动,左右滚轮成角度向上运动,上下滚轮为主转动轮,且采用分片组装式结构[8],左右滚轮在型材的带动下旋转.通过改变左右滚轮的上升位置即可获得不同的滚弯半径的型材弯曲件.在有限元模拟中,材料模型为经典双线随动硬化(BKIN)弹塑性材料模型,型材采用SHELL163单元,滚轮设为刚体.对型材、左右滚轮采用扫略网格,对上下滚轮采用自由网格.各部分材料性能参数见表1.

表1 各部件材料性能参数
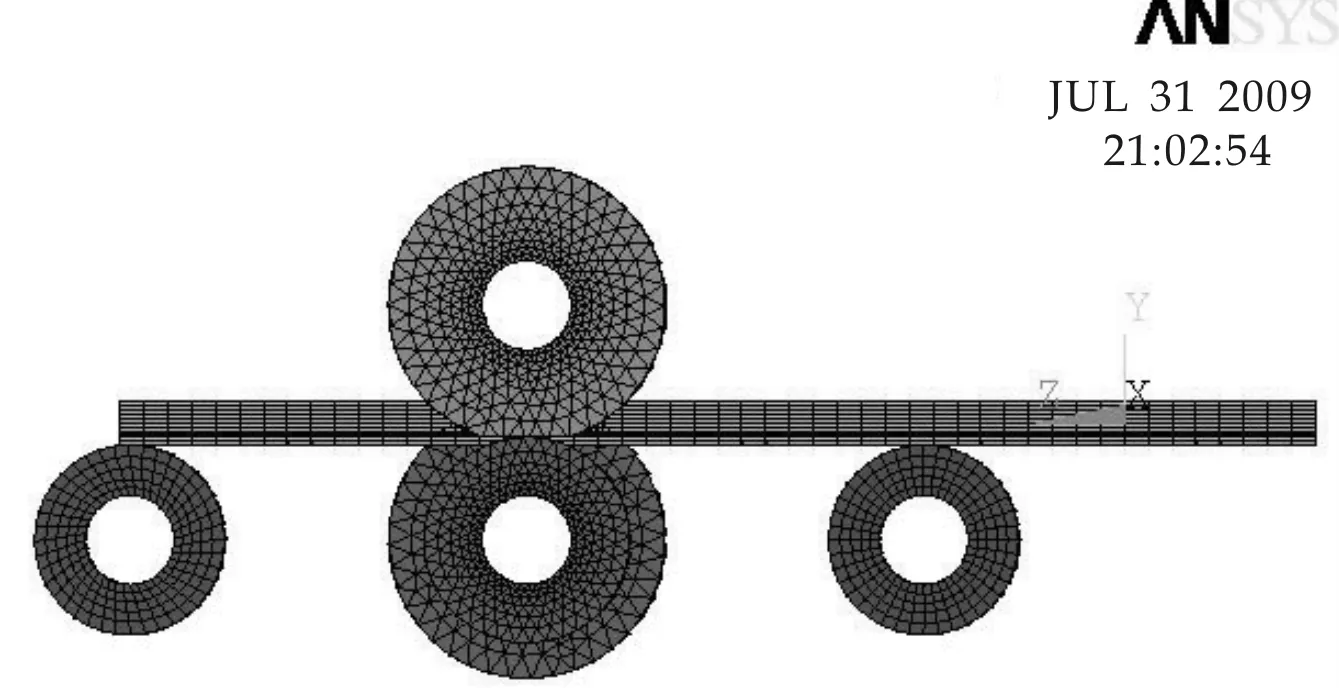
图1 滚弯成形有限元模型
由于在滚弯过程中,型材的进给依靠上下滚轮的摩擦力驱动,故设定上下滚轮绕X轴自转(转向不同),通过设定摩擦系数即可实现型材的进给运动.由于左右滚轮作用在型材上的压力很难测定,而其移动位移易于测量,因此在文中采取对左右滚轮施加位移载荷来模拟滚弯过程.最终滚弯成形模拟如图2所示.通过对模拟结果进行测量可知,滚弯后型材变形区腹板高度减小而其长度却增加.

图2 滚弯成形过程模拟图
2 滚弯成形应力与应变中性层分析
对滚弯区域沿型材中心位置的腹板高度方向(逐步向内)取9个单元,对比分析滚弯过程中腹板高度方向应力与应变随时间变化的分布规律,如图3所示.从图3可以知道:
(1) 沿型材腹板高度方向由外侧到内侧应力、应变变化依次为正值、零值、负值(单元A-I),则最外层受拉应力,最内层受压应力.而根据中性层理论,腹板高度的h/2处为中性层,由图3可知E单元处于中性层位置.
(2) 随着滚弯过程的进行,应力和应变中性:层不断波动,并且随着曲率的增大逐渐向曲率中心方向移动(压应力方向).
(3) 滚弯开始阶段,应力中性层与应变中性层重合,并通过腹板断面重心,随着滚弯进行,应力中性层与应变中性层不再重合,而且应力中性层内移量大于应变中性层内移量.
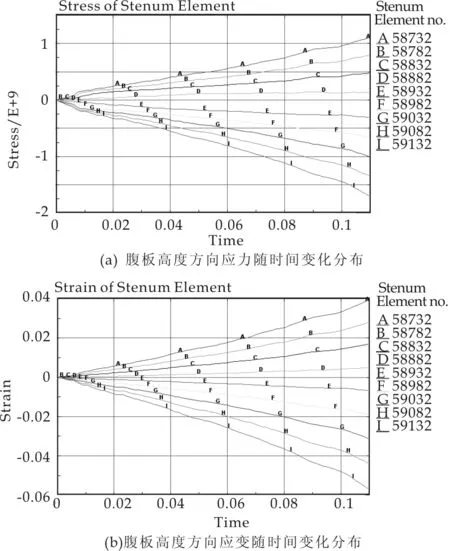
图3 腹板高度方向应力与应变随时间变化分布图
3 回弹前后应力、应变分析
3.1 回弹前后腹板长度方向应力与应变分布
在滚弯加工过程中,型材一部分发生弯曲,另一部分却发生回弹,即回弹也是一个动态过程.所以,型材滚弯过程中的回弹分析比较复杂[9].本文对回弹前后型材腹板长度方向等效Mises弹性应变和应力进行对比分析,结果如图4所示.
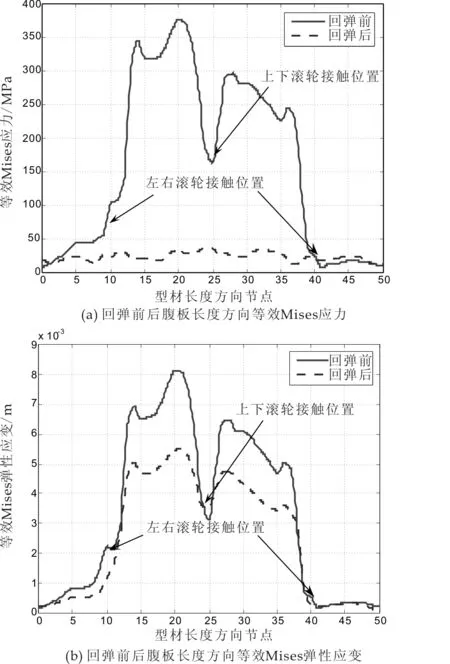
图4 回弹前后腹板长度方向应力与应变分布图
从图示中可以看出在滚弯的过程中,型材逐步经历弯曲-再弯曲-回弹变化过程.结合图a、图b可知,型材滚弯一段后,左滚轮与上滚轮之间的应力和应变大于右滚轮与上滚轮之间的应力和应变,这是因为型材在滚弯的过程中还在向z轴正向进给,因而左侧应力、应变应大于右侧.型材在滚弯开始与上滚轮接触部位应力最大,随着逐步进给,由于摩擦的产生使得应力、应变峰值降低.脱离接触后,由于滚弯过程加深,使得这部分达到新的应力、应变峰值.而在左右滚轮接触的位置,由于滚轮对型材有一向上的力,使得该处在塑性变形区域内应力较小.而应力趋近于零的部分为型材直边部分.
从图示中还可以看出,回弹前后型材与滚轮动态接触过程中存储的弹性能在成形压力消失后释放,使得滚弯区域弹性应变回复,等效Mises应力大大降低.然而,在与上滚轮接触位置,回弹前后等效Mises弹性应变变化最小.
3.2 回弹前后腹板高度方向应力分布
回弹过程起始于卸载阶段,因此,为了更好了解回弹规律,必须结合弯曲成形最终应力变化和卸载过程应力变化[10].由于型材采用弹塑性材料,滚弯成形后,型材在左右滚轮的作用下,型材腹板高度方向上的切向应力分布如图5(a)所示.从图示中可知,成形后,腹板在滚弯拉伸区应力为正,在压缩区应力为负,中性层向内侧移动,且型材在成形过程中经历了从弹性变形到塑性变形的转变.卸载时,根据卸载定理,相当于施加反向弹性弯矩,故其应力呈线性分布,如图5(b)所示.卸载后,将卸载前与卸载时切向应力叠加,可得到回弹后型材腹板高度切向应力变化,其应力如图5(c)所示.

图5 弹塑性弯曲卸载过程中型材腹板高度方向切向应力变化

图6 回弹前后腹板高度方向切向应力对比
本文对有限元模拟结果进行了数值分析,得到了型材腹板高度方向在滚弯成形、回弹两个阶段的切向应力分布状况,如图6所示.从图示中可知,数值模拟结果与上文理论分析结果一致.
4 结论
该文运用显式动力分析软件ANSYS/LS-DYNA成功实现了对飞机Z型材弯曲件滚弯及其回弹过程的数值模拟.通过比较型材切向应力模拟分布与理论变化,发现两者一致,说明采用显、隐式相结合的方法计算弯曲回弹问题是比较成功的.
模拟结果表明:型材变形区腹板高度减少及长度增加,腹板应力中性层和应变中性层内移,回弹后,弹性能释放,等效Mises弹性应变和等效Mises应力的峰值变小,但在型材的起始滚弯位置仍有一个较小的残余应力集中.
[1] 杨建国.大尺寸板材滚弯过程应力场特点分析[J].材料科学与工艺,2008,16(5):684-687.
[2] 孙卫东.数控四轴型材滚弯机应用研究[D].西安:西北工业大学,2001.
[3] 周养萍,亓江文.型材变曲率滚弯过程有限元模拟[J].机械科学与技术,2008,27(8):1113-1120.
[4] 郑军兴.冷弯成形有限元数值模拟及回弹分析[D].昆明:昆明理工大学,2006.
[5] MeiZhan,HeYang,LiangHuang,et al. Springback analysis of numerical control bending of thin-walled tube using numerical-analytic method[J]. Journal of Materials Processing Technology,2006,177:197-201.
[6] S.K.Panthi,N.Ramakrishnan ,K.K.Pathak,et al. An analysis of springback in sheet metal bending using fnite element method(FEM)[J]. Journal of Materials Processing Technology,2007,186:120-124.
[7] 何 涛. ANSYS10.0/LS-DYNA非线性有限元分析实例指导教程[M].北京:机械工业出版社,2006.
[8] 周养萍.型材滚弯成形研究[D].西安:西安理工大学,2007.
[9] 胡军峰,杨建国,方洪渊,等.滚弯过程的三维动态仿真模拟[J].塑性工程学报,2005,12(3):51-55.
[10] 李文平.弯曲回弹变分原理及其数值模拟研究[D].秦皇岛:燕山大学,2006.
