一类含有非线性项的不确定系统的有限时间输出跟踪控制

王 琴, 吴保卫

(陕西师范大学数学与信息科学学院, 陕西 西安 710062)

0 引 言

在控制系统的性能指标中, 收敛性能是很关键的一个指标. 俄国力学家A.M李雅普诺夫于1892年首先提出了运动稳定性的一般理论[1]. 此后, 李雅普诺夫意义下的稳定备受关注, 得到了不同系统下的许多研究结果. 然而, Lyapunov稳定的系统有时在工程上的应用效果并不好, 这就要求人们关注有限时间内稳定的性能指标.

20世纪60年代以来, 连续有限时间控制问题开始受到越来越多的关注[2-4]. 文献[2]针对一类不确定系统, 运用终端滑模控制的理论, 给出了系统有限时间稳定的充分条件； 文献[3]讨论了一类含有时滞项的有限时间稳定问题并设计了反馈控制器, 给出了标量系统有限时间稳定的充分条件； 文献[4]讨论了自治系统的有限时间稳定问题, 最终给出了有限时间稳定的李雅普诺夫稳定定理. 伴随着对有限时间控制问题研究的深入, 有限时间跟踪控制问题也得到了学者的广泛关注[5-9].

本文讨论了一类含有非线性项的不确定系统的有限时间输出跟踪控制问题,利用滑模控制原理设计了滑模控制器, 使得辅助系统的状态在有限时间内到达切换面并维持在切换面上运动, 最后, 利用李雅普诺夫有限时间稳定定理给出了含有非线性项的不确定系统有限时间跟踪信号参考模型输出的充分条件.

1 预备知识及假设

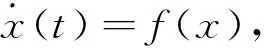
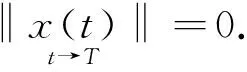
(2) 若t>T时,‖x(t)‖≡0 .

引理[2]若连续正定函数V(t)满足下列微分不等式:

其中,c>0,0<η<1 是两常数, 则V(t)满足以下不等式:

V1-η(t)≤V1-η(t0)-c(1-η)(t-t0),t0≤t≤t1

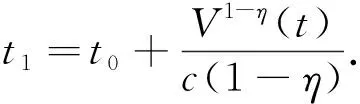
为便于计算, 给出以下假设与引理：

假设1 (A,B)完全能控.

假设2 对于∀x1,x2,f(x)是L2范数有界的且满足

‖f(x1)-f(x2)‖≤ρ‖x1-x2‖

其中ρ是正常数,f(0)=0.

假设3 对非线性控制输入φ(u)需满足以下条件:

uTφ(u)≥αuTu

其中α是非零正常数且φ(0)=0.

2 主要结论

考虑如下的带有非线性项的不确定系统:

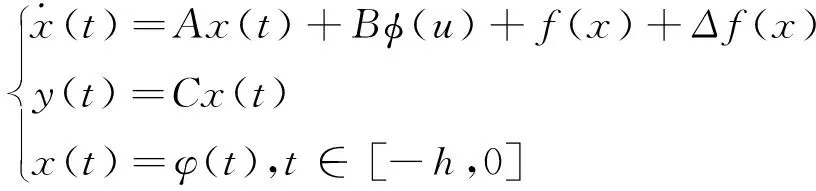
(1)

其中x(t)∈Rn是状态向量,f(·)是非线性扰动输入,u(t)∈Rm是控制输入,y(t)∈Rl是测量输出,φ(t)是一个连续向量值初始函数,φ(u)是一个连续函数,B是列满秩的. 不确定项Δf(x)是范数有界的, 且‖Δf(x)‖≤ρ‖x(t)‖, 其中，ρ≥0.

另外,本文考虑如下形式信号的参考模型:

(2)

其中,xr(t)∈Rm×n是参考信号模型状态向量,G1、H是适当维数的常矩阵,yr(t)与y(t)有相同的维数.

本文的目的是设计滑模控制率u(t)，使得系统(1)的输出可以有限时间跟踪信号参考模型(2)的输出, 类似文献[1], 假设存在G∈Rm×n，使得

HG=C

(3)

为讨论的方便,引入以下新的状态变量z(t)：

z(t)=Gx(t)-xr(t)

(4)

则e(t)=y(t)-yr(t)=Hz(t).

由式(1)、(3)及(4)知：

(5)

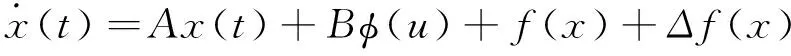
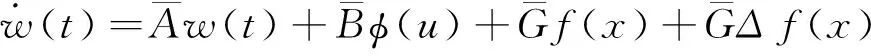
(6)

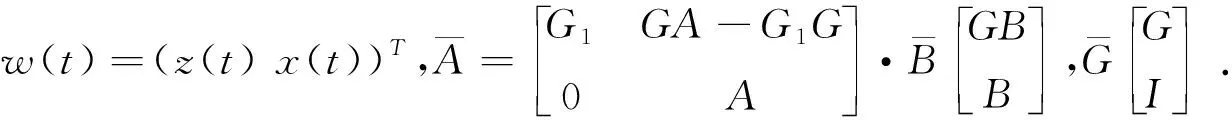
(注释1:要说明系统(1)的输出可以有限时间跟踪信号参考模型(2)的输出，等价于说明e(t)有限时间稳定, 而由式(5)知,事实上e(t)有限时间稳定等价于系统(6)是有限时间稳定的, 为此下文主要考虑辅助系统(6)的有限时间稳定问题.)

为使辅助系统(6)有限时间稳定, 选取终端切换函数:

(7)

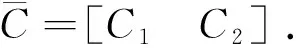
选取滑模控制率为:

(8)

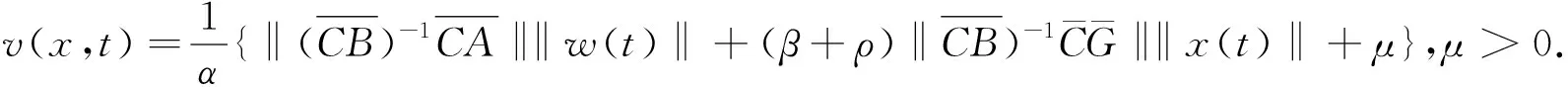
定理1 若切换函数选为式(7), 滑模控制率选取为式(8), 则辅助系统(6)将在有限时间到达切换面s(t)=0上, 并维持在切换面上运动.

证明:取下列形式的Lyapunov函数

(9)

则由式(7)知：

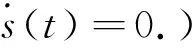
定理2 若切换函数选取为形式(7), 滑模控制率选为形式(8), 如果存在矩阵C1、C3以及可逆矩阵C2,使得下列条件成立,则系统(1)的输出在有限时间内可跟踪信号参考模型(2)的输出.

(10)

且C1B+C2GB可逆.

其中,k=diag{ki(i=1,…,n)},ki≥0,但不全为零.

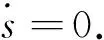
由此可知, 系统的滑动模态为:

(11)

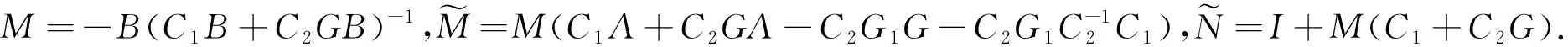
取Lyapunov函数V2=xT(t)x(t)，则由式(10)、(11)及假设知

所以, 由引理知, 系统状态x(t)将在有限时间内到达平衡点.

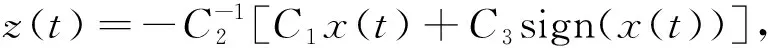
3 算例仿真

设系统(1)和(2)中的矩阵分别为

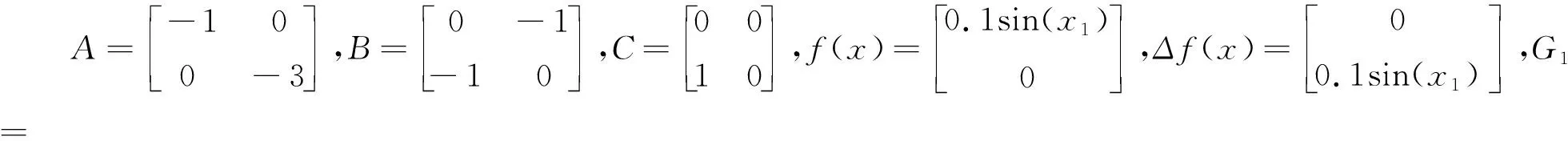
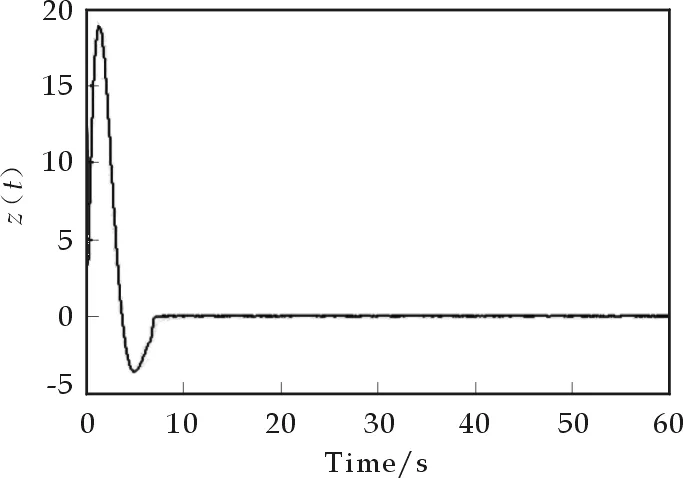
图1 z(t)表示辅助系统 (6)的运动状态

通过Matlab对算例进行仿真,结果如图1所示.

由此可知, 本文提出的含有非线性项的不确定系统的输出跟踪控制方案是可行的.

4 结束语

考虑到跟踪的时效性, 本文讨论了一类含有非线性项的不确定系统的有限时间输出跟踪控制问题. 首先,运用滑模控制理论给含有非线性项的不确定系统设计了滑模控制率, 使辅助系统状态在有限时间到达切换面并维持在切换面上运动; 其次, 给出了辅助系统有限时间稳定的充分条件, 使系统输出有限时间跟踪参考模型输出信号； 最后,通过数值算例演示了该方法的可行性.

参考文献

[1] MING Chang-pai. Design of adaptive sliding mode controller for robust tracking and model following[J]. Journal of the Franklin Institute, 2010, 347(10):1 837-1 849.

[2] WANG Hua, HAN Zheng-zhi, XIE Qi-yue,etal. Finite-time chaos control via nonsingular terminal sliding mode control[J]. Commun Nonlinear Sci Numer Simulat, 2009, 14(6):2 728-2 733.

[3] Emmanuel Moulay, Michel Dambrine, Nima Yeganefar,etal. Finite-time stability and stabilization of time-delay systems[J]. Systems & Control Letters, 2008, 57(7):561-566.

[4] Sanjay P.Bhat, Dennis S.Bernstein. Finite-time stability of continuous autonomous systems[J]. SIAM J.Control Optim., 2000, 58(2): 751-766.

[5] 王 康，沈艳军.一类利普希茨非线性的全局有限时间控制[J].三峡大学学报， 2011, 33(1): 108-112.

[6] JIN Er-dong, SUN Zhao-wei. Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control[J]. Aerospace Science and Technology, 2008, 12(3): 324-330.

[7] CAO Yong-can, REN Wei, MENG Zi-yang. Decentralized finite-time sliding mode estimators and their applications in decentralized finite-time formation tracking[J]. Systems & Control Letters, 2010, 59(9): 522-529.

[8] SU Yu-xin, ZHANG Chun-hong. Global finite-time inverse tracking control robot manipulators[J]. Robotics and Computer-Integrated Manufacturing, 2011, 27(3): 550-557.

[9] 丁世宏，李世华.有限时间控制问题综述[J]. 控制与决策, 2011, 26(2): 161-169.

[10] LIU Lei-po, HAN Zheng-zhi, LI Wen-lin. Non-fragile observer-based sliding mode control for uncertain time-delay systems[J]. Journal of the Franklin Institute, 2010, 347(2): 567-576.