复杂多边形图形矢量数据结构编码方式的改进
2012-02-19邱国清
邱国清
(漳州师范学院计算机科学与工程系, 福建 漳州 363000)
0 前 言
矢量数据结构精度高,易于空间信息的可视化表达[1].多边形矢量编码使边界坐标数据和多边形单元一一对应,各个多边形边界都单独编码和数字化,具有编码容易、数字化操作简单等特点,但它无法解决多边形中嵌套多边形这种复杂的结构.四叉树编码方法的优点在于能弥补多边形矢量编码的缺陷,它允许在多边形中嵌套多边形即所谓“洞”这种结构的存在,但它最大的缺点在于编码转换时具有图形编码的不确定性,用同一形状和大小的多边形可能会得出多种不同的四叉树结构,不利于形状分析和模式识别.为了克服该缺点,本文采用霍夫曼编码的原理,在四叉树编码图的基础上重新进行编码,形成霍夫曼编码树.由于霍夫曼编码是以二叉树来表示的,这样就能保证一组编码只能对应一个霍夫曼编码树,从而防止了同一形状和大小的多边形可能出现多种不同的编码树结构,然后采用Morton码的原理对每个节点进行表示.
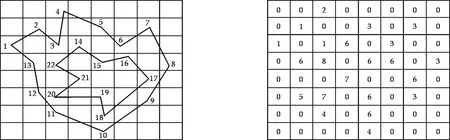
图1 复杂多边形图形 图2 四叉树编码图
1 四叉树编码图
四叉树编码的基本思路是将一幅地图等分成4等分,逐块检查网格属性值,如果某个子区的所有格网值都具有相同的值,则无论该区域值是否相等都同样继续分割,直到每个子块都只含有相同的属性值[2],如图2所示.以图2为例,做以下假设:属性值为1的节点有1、2、3;属性值为2的节点有4;属性值为3的节点有5、6、7、8、9;属性值为4的节点有10、11;属性值为5的节点有12;属性值为6的节点有13、14、15、16、17、18、19;属性值为7的节点有20、21;属性值为8的节点有22.

表1 概率表
2 四叉树编码图转换成二叉树
霍夫曼编码的基本思想[3]是按照字符出现概率的大小编码,概率大的字符分配短码,概率小的字符分配长码来构造最短的平均码长,以图2为例,该图形编码中每个像素元的属性值出现的概率大小计算如表1所示.
表2编码过程
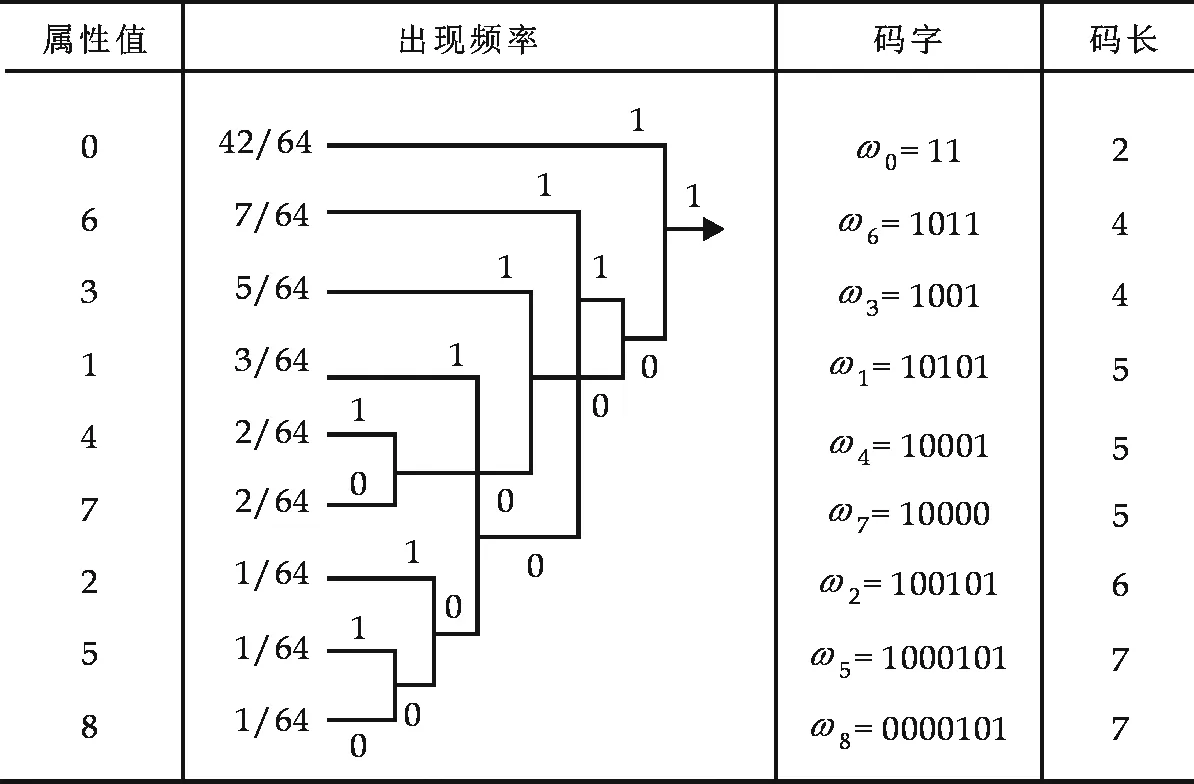
用霍夫曼编码方法对属性值进行编码,其编码过程如表2所示.
表2的编码过程可用图3的编码树来表示.
因为表2中的编码只能得出一棵对应的编码树,从而不会产生形状分析和模式识别的问题.
3 Morton码的原理
Morton码的原理如图4所示, 其计算过程如图5所示.这样就可以行列表示2维栅格阵列图形,用Morton码写成二维数组,通过Morton码来确定节点的坐标.利用Morton码对每个节点数字化时,如果某个节点之前已经完成过一次数字化就不需要再重复数字化和存储,这样就可以保证每个节点只被数字化一次.
节点1对应的Morton码为第1行第5列即18,节点2对应的Morton码为第4行第6列即27,用同样的计算方法可以计算出所有节点对应的Morton码.将Morton码读入二维数组中:
Morton码: 18 27 31 ……
霍夫曼编码: 11 1011 11 ……
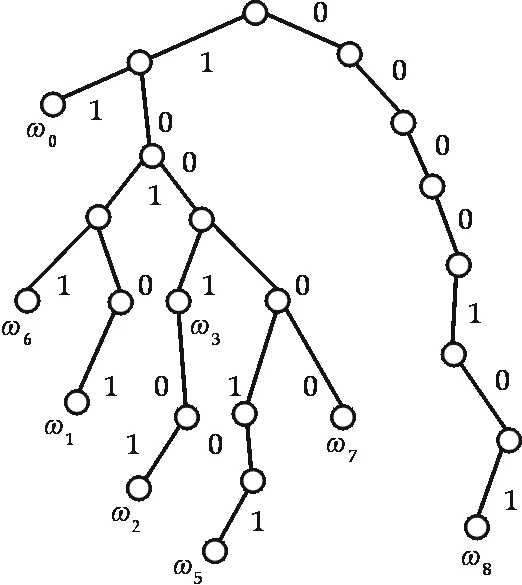
图3 霍夫曼编码树
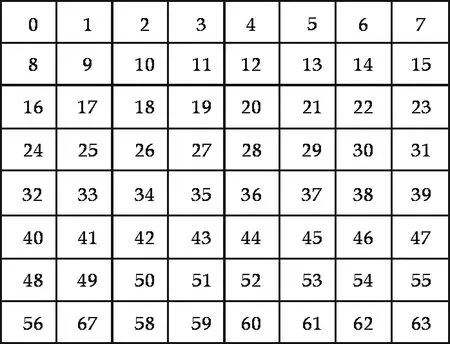
图4 Morton码
4 多边形矢量编码
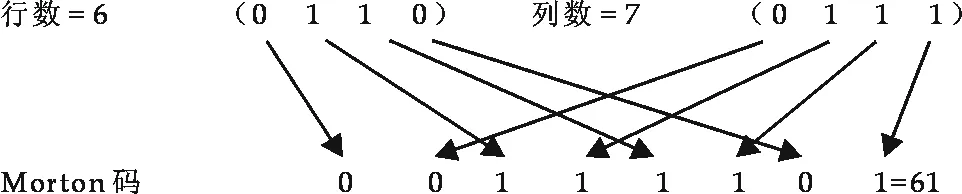
图5 Morton码的计算过程
多边形矢量编码的文件编码坐标为x1,y1;x2,y2;x3,y3;…,所以使用多边形矢量编码来表示时只要将与编码坐标对应的霍夫曼编码值依次写入即可.
霍夫曼编码 11 1011 11 …
多边形矢量编码x1,y1x2,y2x3,y3…
5 结束语
本文利用霍夫曼编码的算法很好地克服了四叉树编码转换时不利于形状分析和模式识别的缺点,研究表明利用Morton码的原理对图形进行压缩编码效果良好.
参考文献
[1] 王 昌,腾艳辉. 矢量栅格一体化数据结构设计与应用[J]. 计算机工程,2010,20:88-89.
[2] 闫浩文. 计算机地图制图原理与算法基础[M].北京:科学出版社,2007:94-95.
[3] 付先平. 多媒体技术及应用[M]. 北京:清华大学出版社,2007:53-55.
[4] 艾自兴,龙 毅. 计算机地图制图[M].武汉:武汉大学出版社,2005:37-45.
