高耗能自解耦式MR阻尼器的设计及性能试验❋

于国军, 杜成斌, 万发学

(河海大学工程力学系 南京,210098)

引 言

MR阻尼器是采用磁流变智能材料制作的一种智能控制装置,其最大优势是可以与计算机结合,根据土木建筑结构的振动响应主动地调节自身参数,使结构振动智能控制的效果最佳。目前,国内、外对MR阻尼器的设计和试验展开了一系列的研究。Yang[1]研制出 200 kN的足尺 MR阻尼器并对其性能进行了试验研究。Spercer等[2]将Sanw a Tekki公司研发的最大阻尼力 400 kN的 MR阻尼器应用于日本Keio大学的一栋隔震居住建筑上。欧进萍等[3]将自行研发的 MR阻尼器应用于山东滨洲黄河大桥斜拉索的风雨振动的控制中;邬华[4]利用 MR阻尼器对斜拉索进行了半主动控制研究;李忠献等[5-6]设计并研究了 MR阻尼器的性能。

到目前为止,高耗能 M R阻尼器还没有得到广泛应用,主要是因为 MR阻尼器仍有一些关键问题没有解决,其中包括磁流变液的沉降稳定性问题、高耗能MR阻尼器的设计及制作上的技术问题。现有MR阻尼器以线性振动结构为控制对象进行设计,对于非线性较弱的情况减振效果明显;而大量的实际结构往往存在较强的非线性,因此,考虑非线性结构振动在内的阻尼器设计方法成为重要的研究内容。在工程应用研究中,常用磁流变液阻尼器去解决常规被动阻尼器也能解决的结构振动控制问题,体现不出MR阻尼器智能控制的优势。为此,笔者提出的阻尼器具有主、副两个活塞,并可根据被控结构位移大小进行阻尼力解耦,具有高耗能的特性,重点研究了高耗能阻尼器设计的关键技术、阻尼器的性能试验及力学模型的参数识别。

1 MR阻尼器的设计原理

传统剪切阀式 MR阻尼器的阻尼力的计算公式[7]为

其中:Ap为阻尼器活塞的有效工作面积;D为活塞直径;Lm为磁流变液工作区域的有效长度;h为工作间隙宽度;fy为磁流变液的剪切屈服强度。

式(1)可看作两项,第1项反映普通流体的黏滞特性,称之为黏滞阻尼力;第2项为库仑阻尼力,是M R阻尼器的可调阻尼力,反映了 MR阻尼器特殊的电控特性。

2 高耗能自解耦式MR阻尼器的设计

对于大多数土木工程应用而言,利用单一活塞的阻尼器作为主动、半主动控制系统的作动装置缺少足够的安全性、节能性和实用性。其具有以下缺陷:a.传统 MR阻尼器在遭遇高频、小振幅情况时易出现刚度硬化现象;b.土木工程结构受地震、风振影响时,传统 MR阻尼器一般都可以在结构振动弹性范围(小位移)内发挥作用,但是结构进入非线性振动,即发生塑性变形(大位移)时,如果没有足够的阻尼力储备,进入塑性阶段直至发生破坏,因为不能随着位移的增大而提供出大阻尼力,此时阻尼器不具备必要的安全保障功能;c.土木工程结构受地震、风载荷影响,需要控制装置发挥作用时间相对于无控时间极短,致使磁流变液成分中固态相颗粒沉降稳定性差,由此带来器件工作不稳定;d.当利用 MR阻尼器作为其控制装置的控制系统出现故障时,MR阻尼器只具备单一的阻尼性能[8],由于磁流变流体的黏度低,根本不具备普通被动油压减振器的阻尼调节功能,此时 MR阻尼器就起不到应有的减振作用,安全性大大降低;e.当 MR阻尼器发挥可调被动功能时,仍需消耗半主动控制系统的能量。

为此,设计了一种高耗能自解耦式MR阻尼器,其实物如图 1所示。

图1 高耗能自解耦式M R阻尼器实物图

2.1 结构设计

高耗能自解耦式 M R阻尼器在常遇地震与高频、小振幅风载荷情况下,具有小阻尼、低动刚度的特性,从而克服了传统 MR阻尼器出现的刚度硬化现象。在罕遇地震即低频、大振幅时,自解耦式 MR阻尼器由于主、副活塞均发挥作用,比传统 MR阻尼器具有更大阻尼力和高耗能的特性,并具有位移控制的优势。高耗能自解耦式M R阻尼器的活塞部分包括主活塞、副活塞,主、副活塞之间通过解耦机制相连。本设计主要针对建筑结构,根据楼层弹塑性层间位移角限值和弹性层间位移角限值的约束条件,确定所设计的阻尼器大、小位移为60和5 mm,经过设计程序的反复调整,确定其他最终主要设计参数如表1所示。结构示意图见图2。

2.2 磁路设计

磁路设计是 MR阻尼器设计的关键部分,磁路设计的优劣直接关系到阻尼器的性能。如导磁、隔磁、永磁材料的选择、导线类型、线圈窗口尺寸、磁极个数、阻尼通道间隙、阻尼通道有效长度等[9]。Gavin等对多阶段活塞上线圈的激励磁场进行了初步研究。关新春[10]对3阶活塞线圈的励磁特性进行了试验及理论分析。杜修力等[11]设计了3阶段活塞的逆变型 MR阻尼器。

高耗能自解耦式 MR阻尼器磁路的基本原理是:在主活塞的磁路部分同时设置励磁线圈和永磁体,由励磁磁场与永久磁场组成复合磁路,线圈采用内绕方式,两线圈并联,线圈通电后产生的磁场对永磁体在阻尼通道中的磁场有增加或削减的能力(线圈产生的磁场方向和永磁体产生的磁场方向一致时在阻尼通道中的总磁场增大;反之减小)。这样可以通过改变线圈电流大小和方向来实时改变阻尼通道中的磁场强度的大小,即可得到可控的阻尼力。在副活塞中只设置永磁体,由永磁体提供磁场,由于主、副活塞中永磁体的设置,给整个主缸体内的磁流变液提供了稳定磁场,通过控制两侧铜制隔磁板的厚度可保证每个活塞左右缸体中的磁场强度在 10～100 m T,从而有利于降低磁流变液的沉降和团聚,在结构形式上提高了磁流变液的稳定性。在线圈和永磁体外壁分别设置铜制隔磁环,可有效防止磁漏,并保证了阻尼通道在各磁极部分的磁场均匀且方向与阻尼器轴线垂直,提高磁场利用率。此外,通过铜制隔磁环的设置可使线圈、永磁体避免与磁流变液的长期接触而腐蚀,从而提高了阻尼器的耐久性。其磁力线分布如图 3所示。

表1 高耗能自解耦式MR阻尼器的主要性能设计参数

图2 高耗能自解耦式M R阻尼器结构示意图

图3 高耗能自解耦式M R阻尼器磁力线分布图

3 自解耦式MR阻尼器的性能试验

为验证高耗能自解耦式 MR阻尼器设计方法的合理性,并对该M R阻尼器的性能进行测评,笔者在电液伺服动静试验机(SDS-300)上对其进行了性能试验。试验采用位移控制方法,输入正弦波曲线,试验工况为不同频率下的简谐振动,循环次数为 10次,试验系统如图 4所示。测试频率从 0.1～ 2.5 Hz,振幅为 5和 60 mm,共组合出 7个大工况,以及 7个大工况下的 63个小工况(同一频率、振幅下改变电流的大小)。以下选取了4个典型频段的试验结果曲线进行分析。

在试验过程中,励磁线圈的电流从 0依次经历-1.0 A和-2.0 A两个过程时,随着反向电流的增大,励磁线圈产生的反向磁场对永磁体所产生的永久磁场的削弱能力增强,使得阻尼器所提供的阻尼力依次减小。励磁线圈的电流从0依次经历1.0 A和 2.0 A两个过程时,随着正向电流的增大,励磁线圈产生的磁场和永磁体所产生的永久磁场叠加,阻尼通道中的磁场强度增强,使得阻尼器所提供的阻尼力依次增大。由采集的数据可以看出,阻尼力的大小是沿着理论上预先设计的方向变化的。图 5中阻尼力-位移关系曲线表示了以上的变化关系。

图4 自解耦式M R阻尼器试验安装图

对于振幅为60 mm的测试工况,重点研究了MR阻尼器在0.1 Hz下阻尼性能;对于振幅为5 mm的测试工况,重点研究了MR阻尼器在0.1,1和2.5 Hz下的阻尼性能。由图5可以得到以下信息:

1)由于电液伺服动静试验机最大输出力为 300 kN,为了能够说明所制作的阻尼器能产生 360 kN的最大输出力,结合图 5(a)的阻尼力-位移关系曲线,将理论结果与能测试到的试验结果的最大值进行比较,如图6所示。结果表明,理论结果与实际结果最大值相差不到5%,说明高耗能自解耦式M R阻尼器完全能够达到最大输出力 360 kN。在与图5(b～ d)阻尼器小位移情况下的阻尼力-位移关系曲线比较可以看出,阻尼器在大位移时的最大输出力是小位移情况下最大输出力的两倍,具备足够的安全储备,满足设计要求。

2)由图 5(a)的阻尼力-位移关系曲线可以看出,实测阻尼力结果与理论计算结果最大值相差较小,所制作的阻尼器最大阻尼力满足设计要求。由于应用在振动控制系统中的 MR阻尼器具有抑制位移响应和加速度响应的优势,所以当结构的速度响应与位移响应方向相反时,速度本身就起到减小结构位移响应的作用,此时如果阻尼力抑制了速度响应,实际反而放大了位移响应。M R阻尼器具有阻尼力与速度无关、可进行实时调节的优点。高耗能自解耦式 MR阻尼器在大位移情况下,由于解耦机制本身短行程的存在,当阻尼力方向与位移方向相反时,滞回曲线在-60～-44 mm和 44～60 mm两个阶段存在凹陷,这对结构进行振动控制是有利的。

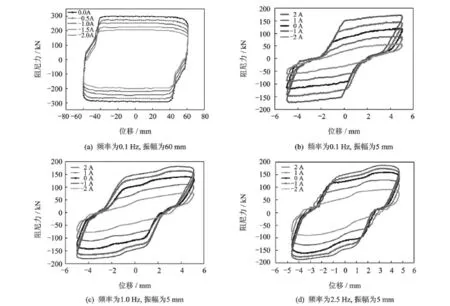
图5 自解耦式 M R阻尼器的阻尼力性能曲线

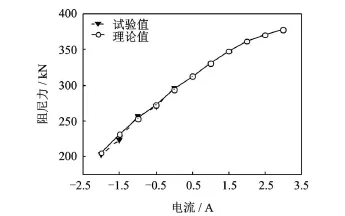
图6 阻尼器外加电流时阻尼力理论与试验值关系比较

3)由图 5(b～ d)的阻尼力-位移关系曲线可以看出,在小位移 (均为5 mm振幅)情况下,解耦机制对磁流变滞回曲线影响明显:当阻尼力方向与位移方向相反时,滞回曲线在这两个阶段的阻尼力很小,达到了阻尼器设计的目的,更适用于土木工程结构的振动控制系统。滞回曲线存在倾斜,这是由于解耦机制中的蝶形弹簧出力叠加在磁流变阻尼力上。

4)从阻尼器的耗能能力,即阻尼力-位移曲线包含的面积可以看出,其耗能性能随着控制电流、频率的增大而增加,高耗能自解耦式 MR阻尼器的耗能能力较好。在小位移情况下,最大、最小阻尼力的比值为5.1,说明MR阻尼器具有较高的阻尼力可调系数倍数,性能较好。

4 阻尼器力学模型及参数识别

4.1 基于反正切函数的MR阻尼器模型

国内、外很多专家在这方面进行了深入研究,取得了一定进展[12]。MR阻尼器的参数化模型虽然多种多样,而且有些能很精确地模拟阻尼器的动态特性,但却无法直接反映阻尼器的逆向动态特性[13]。根据己有的研究结果,提出了一种既简化又能与实际相符合的基于反正切函数的力学模型。依据此模型,阻尼器输出的阻尼力可表示为

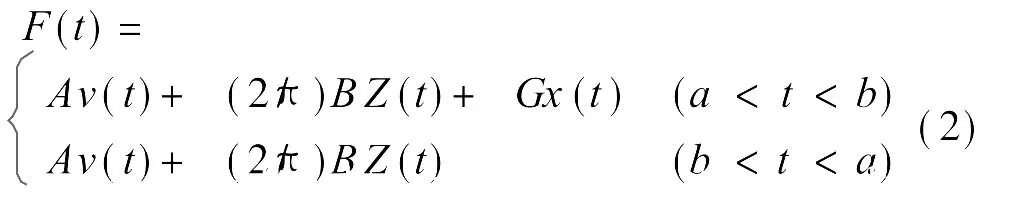
所需识别的参数有 6个,可以根据 MR阻尼器的试验结果,采用参数识别的方法来识别上述表达式中的所有参数,建立力学模型。

4.2 模型参数识别

参数识别问题一般可采用非线性的最小二乘方法,笔者对 MR阻尼器的参数识别采用阻尼最小二乘法。其基本算法思想为:选取初始参数以及允许误差,进而计算目标函数(残差平方和)和观测矩阵,求出初始参数修正值,在新的参数条件下再次计算目标函数,如此反复计算,直到找出最小的目标函数值条件下的参数,即为实际的参数值。

根据此方法,选取试验中的一组数据,其中激励振幅为60 mm,频率为0.1 Hz,识别基于反正切函数的力学模型的6个参数,其识别结果如表2所示。根据识别的结果得到如图7所示的M R阻尼器的理论滞回曲线与试验滞回曲线的比较关系图,从图中可以看出,理论结果与试验结果吻合得很好,因此该参数识别方法是可行和有效的。

表2 阻尼器的动力模型参数

图7 基于反正切函数的 M R阻尼器模型理论值和试验值的比较

5 结 论

1)设计并加工制作了最大输出力达 360 kN的高耗能自解耦式 MR阻尼器,阻尼器的活塞部分包括主、副两个活塞,二者之间通过解耦机制相连。性能测试结果表明,解耦机制对阻尼性能影响明显,阻尼器在大位移时的最大输出力是小位移时最大输出力的两倍,具备足够的安全储备,达到了设计目的。

2)高耗能自解耦式 MR阻尼器的结构、磁路的关键技术研究可为大吨位M R阻尼器的设计和制作提供实践经验和技术参考,为应用 MR阻尼器的土木建筑结构的非线性振动控制设计提供依据。

3)基于反正切函数的力学模型并利用最小二乘法可以有效识别 MR阻尼器的模型参数。试验结果表明,根据理论识别的参数模拟的滞回曲线与试验结果吻合较好。

[1] Yang Guangqiang. Large-scalemagneto-rheologcal fluid damper for vibration mitigation modeling testing and control[D].Indiana,USA:University of Notre Dame,2001.

[2] Spencer B F,Nagarajah S.State of the art of structural control[J].Journal of Structural Engineering,2003,129(7):845-856.

[3] Ou Jinping,Li Hui.Design approaches for active,semi-active and passive control systems based on analysis of characteristics of active control force[J].Earthquake Engineering and Engineering Vibration,2010,8(4):493-506.

Wu Zhehua,Lou Wenjuan,Chen Yong,et al.Optimal marker of M R damper for stay-cable with semiactive vibration control[J]. Journal of Vibration,Measurement& Diagnosis,2006,26(1):41-45.(in Chinese)

[5] 瞿伟廉,刘嘉,涂建维,等.500kN足尺磁流变液阻尼器设计的关键技术[J].地震工程与工程振动,2007,27(2):124-130.

Qu Weilian,Liu Jia,Tu Jianwei,et al.Crucial techniques for design of 500 kN large-scale M R damper[J].Earthquake Engineering and Engineering Vibration,2007,27(2):124-130.(in Chinese)

[6] 邢海军,杨绍普,申永军,等.孔隙阀式磁流变阻尼器准静力分析 [J].振动、测试与诊断,2009,29(4):454-457.

Xing Haijun,Yang Shaopu,Shen Yongjun,et al.Quasi-static analysis of magnetorheological damper with a hole duct valve[J].Journal of Vibration,Measurement& Diagnosis,2009,29(4):454-457.(in Chinese)

[7] 关新春,欧进萍.磁流变耗能器的阻尼力模型及其参数确定[J].振动与冲击,2001,20(1):5-9.

Guan Xinchun, Ou Jinping. Magnetorheological damper′s damping force model and the definition of its parameter[J].Journal of Vibration and Shock,2001,20(1):5-9.(in Chinese)

[8] 熊超,郑坚,张进秋,等.磁流变阻尼器的设计及其力学特性实验研究[J].军械工程学院学报,2004,16(2):1-5.

Xiong Chao,Zheng Jian,Zhang Jinqiu,et al.Design and experimental study on M R damper[J].Journal of the Ordnance Engineering Institute,2004,16(2):1-5.(in Chinese)

[9] 于国军,杜成斌,孙立国.一种新型复合磁流变阻尼器的设计与磁路仿真分析 [J].机械设计与研究,2007,l23(3):113-117.

Yu Guojun,Du Chengbin,Sun Liguo.The design of a new-style composite M R damper and magnetic circuit simulation analysis[J].Machine Design and Research,2007,l23(3):113-117.(in Chinese)

[10]关新春 ,李金海 ,欧进萍.三阶段活塞式磁流变液减振器磁路的试验研究 [J].机械设计与研究,2004,20(1):60-62.

Guan Xinchun,Li Jinhai,Ou Jinping.Experimental studies of magnetic circuit of three stage piston-type magnetorheological fluid damper[J].Machine Design and Research,2004,20(1):60-62.(in Chinese)

[11]杜修力,牛东旭,廖维张,等.逆变型磁流变阻尼器的设计与性能试验 [J].振动与冲击,2006,25(5):49-53.

Du Xiuli,Niu Dongxu,Liao Weizhang,et al.Design and experimental studies on the inverse control magnetorheological damper[J].Journal of Vibration and Shock,2006,25(5):49-53.(in Chinese)

[12]GuoShuqi,YangShaopu,Pan Cunzhi. Dynamic modelingof magneto-rheological damperbehaviors[J]. Journal ofIntelligent MaterialSystems and Structures,2006,17(1):3-14.

[13]邢海军 ,杨绍普 ,郭树起.一种磁流变阻尼器动态阻尼力模型 [J].振动与冲击,2010,29(7):105-108.

Xing Haijun,Yang Shaopu,Guo Shuqi.A dynamic model of magnetorheological dampers[J].Journal of Vibration and Shock,2010,29(7):105-108.(in Chinese)