基于影响系数和滞后角的相位测定含义分析法❋

宾光富, 赵庆亮, 江志农, 高金吉

(1.北京化工大学化工安全教育部工程研究中心 北京,100029)

(2.湖南科技大学机械设备健康维护湖南省重点实验室 湘潭,411201)

引 言

相位对于压缩机、汽轮机等旋转机械振动分析非常重要,相位定义正确与否直接影响到转子动平衡的成败。人们以前大都只重视振动的幅值,即以振动的大小作为振动监测、分析和状态检测的依据。这种方法虽然在多数情况下有效,但在一些比较复杂的转子系统结构和特殊工况下,却掩盖了很多振动现象,造成技术人员的误解。随着现代测试技术的飞速发展,具备振动相位分析功能的振动仪已开始在工程实际中广泛应用[1]。由于振动相位的概念比较抽象,不易直观理解,且目前国内使用的振动仪种类和型号较多,不同的生产厂家对振动相位的定义标准各不相同,甚至同一系列产品的相位定义含义也不一样,这就使国内技术人员对振动相位含义的理解和实际应用更加困难。因此,笔者结合比利时LM S测试系统,详细介绍了相位的基本概念、测量原理和方法,采用逆向反推法,提出一种基于影响系数和滞后角的振动仪相位含义分析新方法。

1 振动仪相位测定分析原理与方法

相位通常是指振动信号上某点(例如峰值或零点等)与转轴上某一标记之间的相位差。目前,国内、外比较通用的相位定义是标准脉冲信号前沿导前振动信号第1个正峰值的角度,即脉冲信号在前,振动信号正峰值在后。

对于一台崭新或者长久未用的振动测试仪,了解和校核其振动相位的具体含义成为进行动平衡试验的首要问题。在获取标准脉冲信号的前提下,关键是如何确定标准脉冲信号前沿是导前还是滞后于振动信号,以及振动仪的相位读数是指标准脉冲信号与振动信号上第1个正峰值、负峰值、正向零点还是负向零点的夹角。

1.1 基于影响系数的不平衡方向确定方法

采用影响系数法确定标准脉冲信号与振动信号导前还是滞后的关系,其基本步骤如下:首先,转子不加重,启动转子至选定转速,测量转子轴承或转轴处的原始振幅值和相位,其矢量用A0表示。试加重量P至转子上,然后重新启动至与第1次相同的转速时,测量试加重量后的振动和相位,其矢量用A01表示。则转子上应加平衡重量Q为

其中:A1为加重效应,表示转子上加了试重P所产生的振动矢量;T为影响系数,表示在转子上加单位质量,加在零度方向、半径为 1 m处或固定半径处,在某一个振动测点上所呈现的振动矢量。

其关系如图 1所示[2]。

图1 测相平衡法矢量图

由图 1可知,要平衡A0,必须把A1移动W角,即把试重P移动W角,而P的移动方向则由平衡仪测量振动相位原理来决定。若平衡仪振动相位读数增大表示不平衡方向滞后,则P需逆转向移动W角,才能平衡A0;若振动相位读数增大表示不平衡方向导前,则P需顺转向移动W角,才能平衡A0。根据该原则,分别按照标准脉冲信号前沿导前或者滞后于振动信号两种情况,对转子试加重量。通过计算影响系数T和配重Q,若配重后振动有明显降低(由于影响系数具有一定的分散性和计算误差,配重后振动不可能降为零),则可以判断出平衡仪振动相位表示的含义,即不平衡方向是滞后还是导前于标准脉冲信号前沿。同时,通过试加重也确定了不平衡方向位置。

1.2 利用滞后角反推振动相位含义

一般地,对一个单圆盘转子系统,滞后角的定义为振动响应滞后于激振力的角度,其定义表达式为[3]

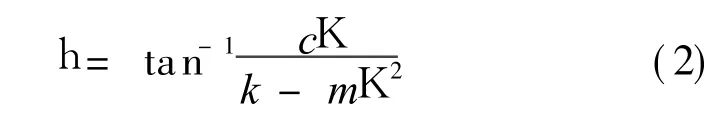
其中:K为转速;m为质量;k为刚度;c为阻尼;O为滞后角。

对于一个试验转子或者现场实际机组,由式(2)可见滞后角只与转子平衡时转速、质量、刚度和阻尼等有关。当k=mK2时,h=90°,即临界转速下其系统滞后角均为90°。故可利用转子起停车Bode图,找出临界转速下振动相位测量值来快速识别出振动相位的定义。

为不失一般性,在确定转子不平衡力方向的前提下,依据滞后角的定义,反向推出振动响应的正高点,然后按照标准脉冲信号前沿导前或滞后于振动信号的关系,即可分析出测振仪所测得的转子同频振动的相位含义(这里不考虑测振仪和振动传感器的滞后角以及测量误差,实际上目前的测振仪对相位测量的精度已经完全可以满足工程需要[4])。因此,利用滞后角和不平衡方向确定振动相位含义可分两种情况进行讨论分析。

情况 1 若标准脉冲信号前沿导前于振动信号上某一点,则基本原理和方法如下:

1)由平衡重量Q可以推出不平衡U,然后以不平衡U方向为起点,逆转向标出滞后角T,即可得出振动信号上第1个正高点H(也即正峰值)。

2)以振动信号上第1个正高点H位置为起点,顺转向与拾振器S标出的夹角为h′,若反推相位角h′与拾振器S实测的角度h大小相等,则该测振仪的相位定义为标准脉冲信号前沿导前于振动信号第1个正峰值的角度 ,如图 2(a)所示;若h′=h-180°,则该测振仪的相位定义为标准脉冲信号前沿导前于振动信号第1个负峰值的角度,如图2(b)所示;若h′=h-270°,则该测振仪的相位定义为标准脉冲信号前沿导前于振动信号第1个正向零点的角度,如图 2(c)所示;若h′=h-90°,则该测振仪的相位定义为标准脉冲信号前沿导前于振动信号第1个负向零点的角度,如图 2(d)所示。

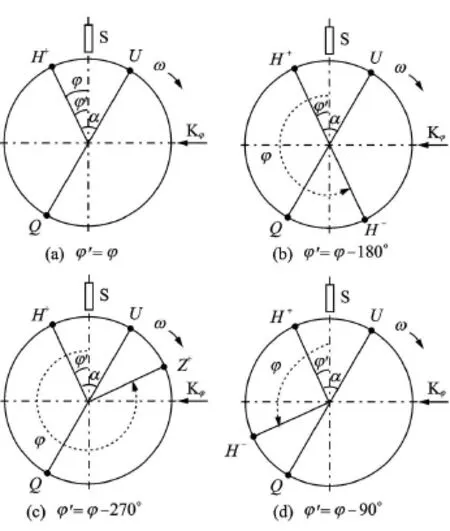
图2 脉冲信号导前振动信号的相位含义确定方法

情况 2 若标准脉冲信号前沿滞后于振动信号上某一点,则基本方法和过程如下:

1)由平衡重量Q可以推出不平衡U,然后以不平衡U方向为起点,逆转向标出滞后角T,即可得出振动信号上第1个正高点H。

2)以振动信号上第1个正高点H位置为起点,逆转向与拾振器S标出的夹角为h′,若反推相位角h′与拾振器S实测的角度h大小相等,则该测振仪的相位定义为标准脉冲信号前沿滞后于振动信号第1个正峰值的角度 ,如图 3(a)所示;若h′=h+180°,则相位定义为标准脉冲信号前沿滞后于振动信号第1个负峰值的角度 ,如图 3(b)所示;若h′=h+270°,则相位定义为标准脉冲信号前沿滞后于振动信号第1个正向零点的角度 ,如图 3(c)所示;若h′=h+90°,则相位定义为标准脉冲信号前沿滞后于振动信号第1个负向零点的角度,如图 3(d)所示。

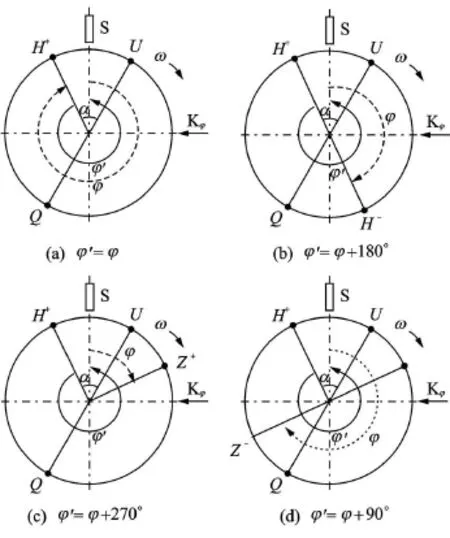
图3 脉冲信号滞后振动信号的相位含义确定方法

2 振动相位测定试验与分析

LM S测试系统是针对振动噪声试验与工程的集成解决方案,具有旋转机械的扭振分析、结构与声学试验、环境试验等功能,集数据采集、试验数据处理、试验报告生成和数据共享于一体,且易于使用,测量精度高。笔者结合LMS测试系统,通过试验,采用基于影响系数和滞后角的振动相位测定分析方法来分析和确认该系统振动相位测定的含义。

2.1 试验装置简介

试验装置如图 4所示,由 Bently转子试验台RK4系统和 LMS测试系统组成。其中 Bently转子实验台 RK4系统主要包括 0～ 10 000 r/min的直流电机、交流调速器、转动轴、弹性联轴节、滑动轴承、转盘(转盘半径为 30 mm的圆周均布16个螺孔)、键相器、安全罩、电涡流传感器、振动传感器支座以及一些可选件。标准脉冲信号前沿采用涡流位移传感器和键槽来获取。

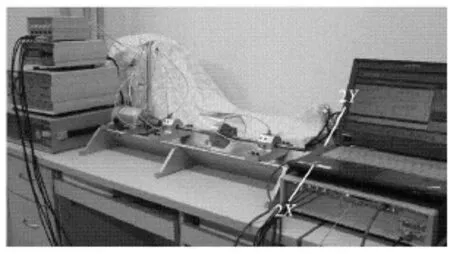
图4 Bently转子试验台

2.2 振动仪相位测定分析试验

考虑到Bently转子试验台正常空转时,转轴2#测点处水平和垂直方向的最大振幅均不超过 12 μ m,原始不平衡量很小,故在转盘半径为 30 mm的 0°方向加 1个 2.15 g螺钉 (规定以键槽开口为 0°方向),以模拟初始不平衡激励力。在稳态转速2 200 r/min下,测取2#测点处转轴振动信号。在转盘 90°方向、半径 30 mm处试加 1个 2.15 g螺钉,在稳态转速 2 200 r/min下,测取 2#测点处转轴的振动信号,其中转轴方向从非驱动端看为顺时针方向。LMS测试软件基本参数设置如下:采样频率为 1 024 Hz,频率分辨率为 1 Hz,谱线数为 1 024,测量记录 10 s的数据。将2#测点记录的20个数据取平均,整理并计算其影响系数和配重如表 1所示。

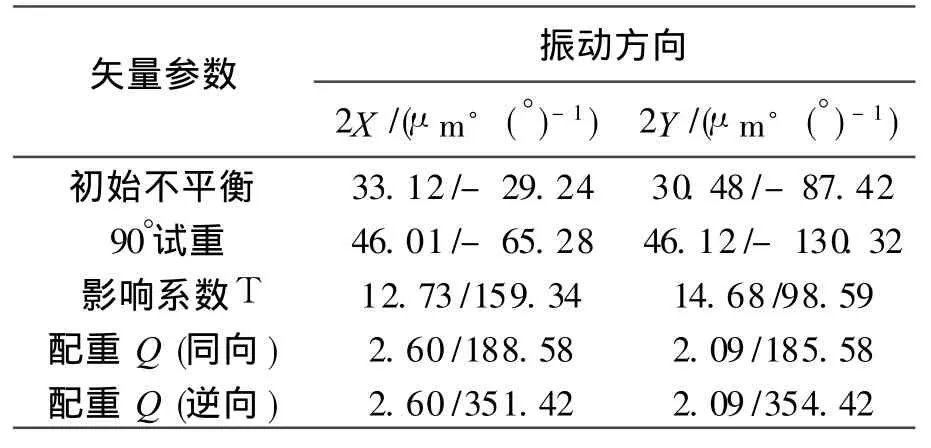
表1 基于影响系数的不平衡方向分析数据

当计算的配重Q为同向时,根据表1中2X和2Y方向的计算数据结果,将试重P移至转盘上 180°方向,测得转轴2#测点处水平和垂直方向的振动明显比初始不平衡振动小60%以上,即配重方向正确,这也与实际不平衡方向(0°方向)相符合,可判断出LM S振动测试仪的相位为标准脉冲信号前沿滞后于振动信号上某一点,且不平衡方向为0°方向。

为避免计算滞后角,笔者通过转子起停车 Bode图,利用临界转速下滞后角均为 90°的特性来快速识别出 LMS测试系统的相位定义是标准脉冲信号前沿与振动信号上哪一点之间的相位差。

在同样的试验条件和环境下,测取转轴2#测点处的振动 Bode图,如图 5所示。

图5 原始不平衡 1 000～ 3 600r/min下 2#测点 Bode图

从图5中可以清晰看出,2X方向的临界转速发生在 2 730 r/min左右,振动为 82.22/-96.12°;2Y方向的临界转速发生在 2 630 r/min左右,振动为99.02/173.72°,按照脉冲信号滞后振动信号的相位含义的推算方法,分析结果如表2所示。由于轴承X,Y向的支承动刚度不一致,以及角度校准时存在误差等其他因素影响,测量相位角与理论值会存在一定差异。

表2 基于脉冲信号滞后振动信号的相位数据分析结果

通过表 2中转轴 2#测点处水平方向和垂直方向的拾振器的数据分析,均可以快速判断出该测振仪的相位定义为标准脉冲信号前沿滞后于振动信号第1个负峰值的角度。

3 结束语

笔者提出一种基于影响系数和滞后角来分析和确定振动仪振动相位含义的新方法,它充分利用了转子动力学和数学矢量线性特性,无需其他已知振动相位定义的标准振动仪作为参考和比较。结合LMS测试系统,通过试验表明,该方法具有操作步骤简单、现场应用方便、计算速度快等优点,对正确判断旋转机械振动相位的具体含义和现场动平衡应用测试分析具有一定的指导意义和实用价值,也可推广到其他相位定义测量与诊断分析过程中。

[1] 李燕,王维民,高金吉.超重力机自动平衡系统的设计及模拟试验研究[J].振动、测试与诊断,2010,30(1):16-18.

Li Yan,Wang Weimin,Gao Jinji.Design of automatic balance system for a high gravity machine and its test[J].Journal of Vibration,Measurement&Diagnosis,2010,30(1):16-18.(in Chinese)

[2] 施维新,石静波.汽轮发电机组振动及事故 [M].北京:中国电力出版社,2008:195-197.

[3] 钟一愕,何衍宗,王正,等.转子动力学 [M].北京:清华大学出版社,1987:3-6.

[4] 王维民,高金吉,江志农,等.旋转机械无试重现场动平衡原理与应用[J].振动与冲击,2010,29(2):212-215.

Wang Weimin,Gao Jinji,Jiang Zhinong,et al.Principle and application of notrial weight field balancing for a rotating machinery[J].Journal of Vibration and Shock,2010,29(2):212-215.(in Chinese)