船用隔离器的低频振动试验❋

史冬岩, 石先杰, 任龙龙

(哈尔滨工程大学机电工程学院 哈尔滨,150001)

引 言

磁流变阻尼器由于具有出力大、温度适应性强、响应速度快、能耗低、结构简单、阻尼力连续顺逆可调并可方便地与微机控制结合等优良特点,已成为汽车、机械装置、桥梁以及土木建筑等领域新一代的高性能和智能化的减振装置。部分装置已经应用于实际工程,展现出了良好的应用前景[1-3]。虽然磁流变阻尼器在工程上已有一定的应用,但在船舶减振方面的研究还较少。当前,在船用隔离器研制中,低频减振是该研究领域的难点。若将一种阻尼器与一种减振器相配合组成一种新的隔离器,这种隔离器若能提高船用隔离器的低频减振效果,将对改善舰船的隐蔽性、生命力和战斗力具有重要的理论和实践意义。

笔者提出了一种由传统的钢丝绳减振器与磁流变阻尼器(简称 MR阻尼器)组合而成的隔离器系统,旨在对舰船基座传统的被动式隔离器进行改造,加强减振系统的低频减振效果。通过对船用隔离器进行振动试验,得到一系列性能曲线。根据试验结果,分析了船用隔离器低频振动性能,为其实际应用提供了参考。

1 船用隔离器

1.1 隔离器设计思想

笔者提出的具体设计方法是:在柔度大、变形能力强的传统减振元件基础上并联智能出力元件,构成新的船用隔离器系统,使隔离器系统的动力学特性由固定不变转为智能可控,再配以适当的控制算法,即可根据激振力的变化而调整系统的出力状态,实现最佳的隔振效果。其原理如图1所示。该隔离器的优点是:a.减振频带宽,可弥补传统大柔度隔离器在低频减振方面的不足;b.充分发挥大柔度隔离器在抗冲击时的优越性,避免了冲击过程中由于隔离器变形过大而产生的二次碰撞。

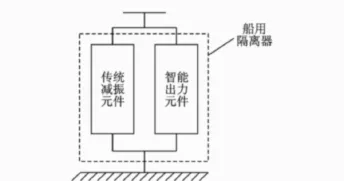
图1 船用隔离器原理图

1.2 钢丝绳弹簧和磁流变阻尼器

钢丝绳弹簧是近几年发展起来的一种新型减振元件,具有相当大的挠度和较大的阻尼,能适应恶劣的环境[4]。其单独应用于舰船主机减振时存在以下不足:a.主机处于某些特定工作状态时会引起剧烈的振动响应;b.由于对称布置的钢丝绳弹簧受力不均匀,会引起主机倾斜,甚至会引起受压力较大一侧的钢丝绳弹簧发生较大塑性变形。

磁流变液是一种新型智能材料,由它设计而成的磁流变阻尼器(简称 MR damper)已成为新一代的减振装置[5-6]。当其安装在结构上时,根据受控结构的振动状态,按照一定的控制规则迅速自动调整阻尼器参数(阻尼),从而抑制结构的振动响应,可以作为一种理想的智能控制装置[7-8]。

2 船用隔离器振动试验

2.1 振动试验系统

笔者设计的船用隔离器系统的物理模型如图 2所示,它主要由以下几部分组成:a.模型下部结构用于模拟船底;b.模型上部结构作为承载设备;c.磁流变阻尼器和钢丝绳弹簧,将模型上、下部结构连成整体,是系统减振抗冲的主要元件;d.侧向限制结构,用于限制上部结构的水平方向运动。

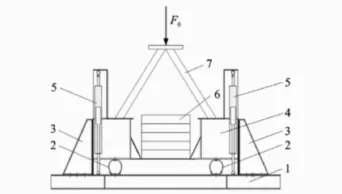
图2 系统模型侧向示意图

在进行振动试验时,将模型的下部结构固定于地面,模拟船底结构。在模型的上部结构上施加竖直方向的激振力以模拟主机振动载荷,激振力通过额定载荷为 10 kN的 MTS液压伺服加载系统施加给隔离器系统,加载系统的作动筒与模型之间通过传力杆连接。振动试验系统如图3所示。

图3 振动试验系统

振动试验输入的激振载荷波形为

振动试验的工况设定为:a.输入系统激振力的力幅为24 kN,激振频率为1～ 15 Hz共15个状态;b.整个模型系统的控制质量划分为 1 000,1 200,1 400,1 600,1 800,2 000 kg共 6个状态;c.将磁流变阻尼器的控制电流划分为 0,0.25,0.5,1.0,1.5,1.75,2.0 A共 7个状态。将上述状态进行组合,共计630个工况。

2.2 振动试验结果

对试验工况各个状态进行的测试表明,在设定的边界条件下,试验模型总体表现为竖直方向的运动。在低频状态时,结构的位移响应及磁流变阻尼器的出力较大,高频状态时较小。 MTS液压伺服加载系统所施加的激振信号在频率上与设计输入相符合,但是力幅在高频状态下有一定的衰减。

2.2.1 磁流变阻尼器的出力特性

由实测磁流变阻尼器出力曲线(图4)可以看出,在简谐激振力作用下控制电流恒定时,其出力过程可近似为一条正弦曲线。这说明在振动试验中,磁流变阻尼器的作用是给模型系统增加了一个阻尼。实测的磁流变阻尼器在不同电流状态下的出力幅值如图5所示。

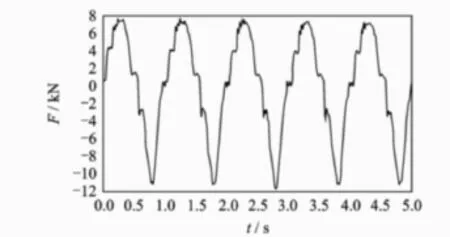
图4 施加控制电流2A时磁流变阻尼器的出力曲线

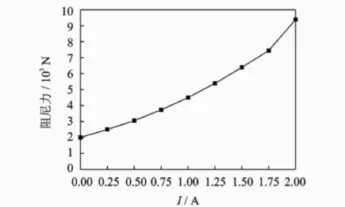
图5 磁流变阻尼器出力与电流之间的关系

根据阻尼力幅值的计算公式,按照实测的数据进行计算,可得出磁流变阻尼器对应各个电流的阻尼,如图6所示。该阻尼的变化规律符合二次多项式的情况,其拟合方程式为

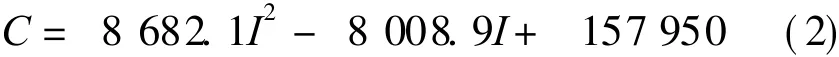
此现象表明,线性地改变磁流变阻尼器的电流相当于以二次函数改变隔离器系统的阻尼系数。

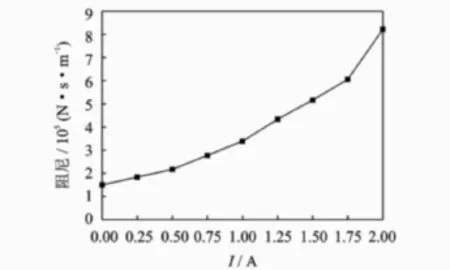
图6 磁流变阻尼器阻尼与电流之间的关系

2.2.2 振动响应与激振频率的关系

下面列出了模型控制质量为 2 000 kg,激振力为24 kN的典型工况的试验结果。图7～图9分别给出了力传递率、位移放大系数和加速度的典型特征曲线。由图可知:

1)在频率不变的情况下,系统的力传递率、位移放大系数、加速度幅值随着电流的增加而不断减小;

2)系统的力传递率、位移放大系数、加速度幅值出现了3个峰值,经试验测得它们分别在频率比为 0.4,1和 1.3,即 4,10和 13 Hz左右;

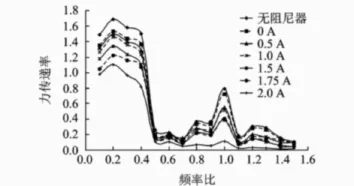
图7 力传递率与频率比的关系曲线

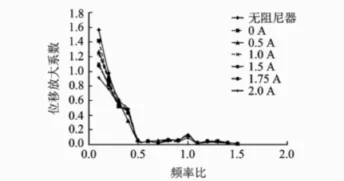
图8 位移放大系数与频率比的关系曲线

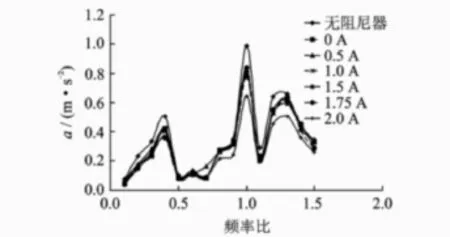
图9 加速度与频率比的关系曲线

3)系统的力传递率、位移放大系数总体表现为在低频处较大,在高频处较小。

3 船用隔离器振动特性分析

根据振动试验结果对隔离器系统的振动特性进行分析,分析所采用的数据为模型的控制质量,即2 000 kg的典型工况的数据结果。

3.1 振动响应与激振频率的关系

1)对隔离器模型的控制作用主要体现在对振动峰值的抑制上,其数值见表1。将未安装磁流变阻尼器与安装磁流变阻尼器未施加控制电流时对数据进行对比,系统的最大力传递率有了一定的降低,这主要是磁流变阻尼器的初始阻尼作用于系统的结果。控制电流逐渐增大,力传递率随之减小。当控制电流达到额定电流 2 A时,力传递率降到最低,数值为1.1。可见磁流变阻尼器对系统力传递率的峰值具有较好的控制效果,与没有磁流变阻尼器时相比较,响应峰值降低了34.5%。位移放大系数的控制规律与力传递率的控制规律基本相同,在没有安装磁流变阻尼器与安装磁流变阻尼器未施加控制电流时相比,系统最大的位移放大系数也有了一定的降低。当控制电流达到额定电流 2 A时,位移放大系数降到最低,数值为1.1。在磁流变阻尼器的控制下,响应峰值最大可降低41.2%。试验结果表明,隔离器系统在低频减振方面具有较好的作用效果,与单独使用钢丝绳弹簧相比有了较大程度的改善。这是因为在频率较低时,增加系统阻尼可以降低系统的振动响应。

2)试验振动响应峰值主要在3～ 5 Hz和10 Hz附近。动态特性测定试验结果表明,竖直方向的固有频率分别为6.1和13.2Hz。这是因为加载系统启动时的系统调零过程对隔离器系统产生了预压,使系统产生较大的变形,钢丝绳弹簧的刚度减小,造成系统的固有频率下降。实测结果显示,该预压引起的钢丝绳弹簧变形为 4～ 5 mm,这使单个钢丝绳弹簧的刚度从226 244.3 N/m降低到154 601.8 N/m,从而使系统的刚度降低了 32%,即实际激振时系统的固有频率降低为原状态的0.82倍。结合动态特性测定试验结果可知,实际激振时隔离器系统的前两阶固有频率应该为 5和 10.82 Hz,这与试验结果较为符合。

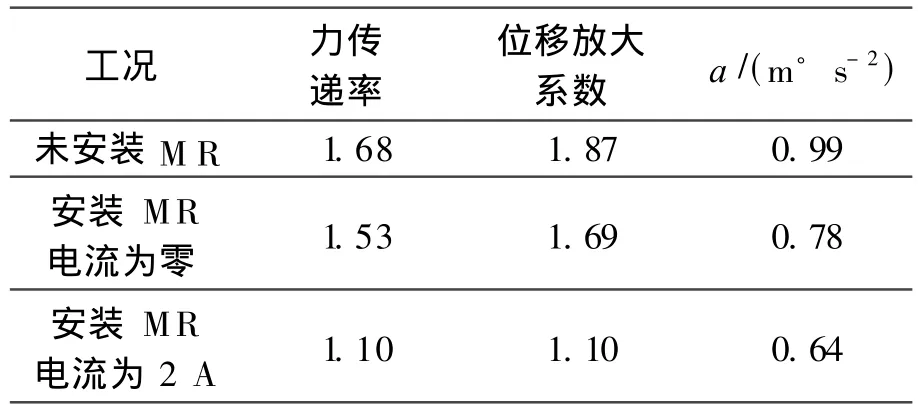
表1 安装磁流变阻尼器前、后振动响应峰值的变化

3)低频时的峰值明显高于高频时的峰值,这主要是因为加载系统的作动筒出力方式是以激振频率达到要求为目标。当激振频率较高时,激振力的实际力幅出现了较大衰减,衰减情况见图10。图中:Fi为输入给作动筒的激振力幅值的指令值;Fo为作动筒实际输出的激振力幅值。

按照激振力衰减情况对力传递率与频率关系曲线图进行转换,可得实际的力传递率与频率比关系曲线,如图11所示。当频率比等于 1时,最大力传递率发生在无阻尼器时,其值为6.36,最小力传递率发生在阻尼器电流为 2A时,其值为 0.9,减幅达到了85.85%。

4)由竖直方向加速度响应曲线可看出,振动响应的峰值更明显地体现在频率比为0.4,1和1.3处,即固有频率为 4,10,13 Hz附近,这与在分析力传递率时所得结论相一致。

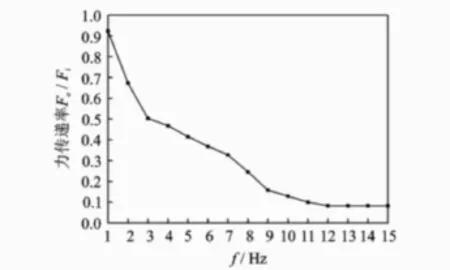
图10 激振力的衰减曲线

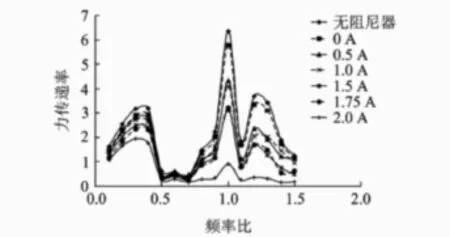
图11 转换后的力传递率与频率比的关系曲线

3.2 振动响应与控制电流关系的变化规律

下面给出控制质量为 1 000,1 600,2 000 kg状态下,试验时的位移响应随电流的变化关系的典型曲线。系统的位移响应整体表现为随电流的增大而减小,并且在振动位移响应较大时,响应曲线明显表现为一条上凸的曲线,如图 12所示。这说明随着电流的增大,电流的变化对振动响应的影响能力在增强。经研究发现,振动的位移幅值与电流的关系为平方关系,其理论关系曲线见图13。可见,实测曲线与理论计算曲线所显示的规律是一致的。

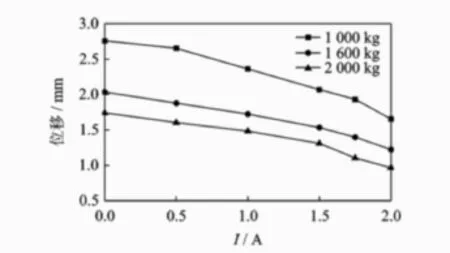
图12 位移与电流的关系曲线

图13 位移与电流的理论关系曲线

3.3 振动响应与控制质量关系的变化规律

激振力为24 kN,控制电流为0,1.0,2.0 A状态下,位移响应随质量的变化关系曲线如图 14所示。由曲线的变化趋势可以看出,在各种电流状态下,系统的振动响应均表现为随控制质量的增加而减小。在控制质量由 1 000 kg增加至 2 000 kg时,振动响应的降幅见表 2。

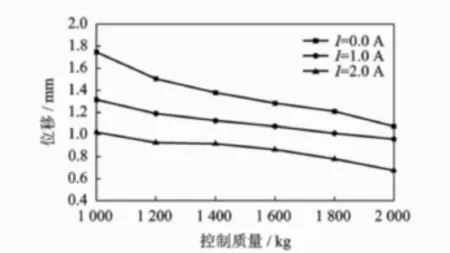
图14 位移与质量的关系曲线

表2 由质量变化引起的振动响应降幅

由强迫振动的位移响应的计算式可知,在其他条件固定的情况下,振动系统质量的增加会降低系统的振动响应。

4 结 论

1)基于现有的船舶减振元件——钢丝绳弹簧和智能出力元件磁流变阻尼器设计的船用隔离器系统的结构形式是合理的,经振动试验验证,船用隔离器系统的动力学响应正常。

2)磁流变阻尼器与钢丝绳弹簧相并联构成的减振系统对低频振动响应有较好的控制作用,力传递率的减幅可达 85.85%,隔振效率较好。

3)磁流变阻尼器对系统的控制作用在激振载荷幅值较大、频率较低时更加明显。

[1] 郭日修,索志强.我国船舶振动研究的回顾与展望 (下)[J].振动与冲击,1989(2):66-69.

Guo Rixiu,Suo Zhiqiang.The review and prospect of study on ship vibration in China(Ⅱ)[J].Journal of Vibration and Shock,1989(2):66-69.(in Chinese)

[2] Choi S B,Lee S K,Park Y P.A hysteresis model for the field-dependent damping force of a magnetorheological damper[J].Journal of Sound and Vibration,2001,245(2):375-383.

[3] Nam Y J,Park M K.Electromagnetic design of a magnetorheological damper[J].Journal of Intelligent Material Systems and Structures,2009,20(2):181-191.

[4] Spencer B F, Dyke S J, Sain M K, etal.Phenomenological model for magnetorheological dampers[J]. Journal ofEngineeringMechanics,1997,123(3):230-238.

[5] 周云,徐龙河,李忠献.半主动磁流变阻尼器控制结构的地震反应分析[J].地震工程与工程振动,2000,20(2):107-111.

Zhou Yun,Xu Longhe,Li Zhongxian.Earthquake response analysis of half-active control on magnetorheological dampers [J]. Earthquake Engineering and Engineering Vibration,2000,20(2):107-111.(in Chinese)

[6] Gordaninejad F,Saiidi M,Hansen B C,et al.Control of bridges using magnetorheological fluid dampers and fiber-reinforced,composite-material column[C]∥Proceedings of the1998SPIE Conference.San Diego:SPIE Society of Photo-Optical Instrumentation Engineers,1998.

[7] 关新春,欧进萍.磁流变耗能器的阻尼力模型及其参数确定 [J].振动与冲击,2001,20(1):5-8.

Guan Xinchun, Ou Jinping. Magnetorheological damper/s damping force madel and the definition of its parameter[J].Journal of Vibration and Shock,2001,20(1):5-8.(in Chinese)

[8] 姚熊亮.船舶振动[M].哈尔滨:哈尔滨工程大学出版社,2004:320-350.