严格伪压缩映像不动点和均衡问题的公共元的迭代算法

刘立红， 陈东青， 冯光辉

(军械工程学院 基础部，河北 石家庄 050003)

0 引言

设H 为一实Hilbert 空间，C 是H 的非空闭凸子集，F(T)={x∈H|Tx =x}表示映像T 的不动点集。设φ∶ C→R 为一实值函数，f∶ C×C→R 为二元均衡函数，即f(u，u)=0 对任意u∈C 成立。混合均衡问题指的是:寻找x*∈C 使得

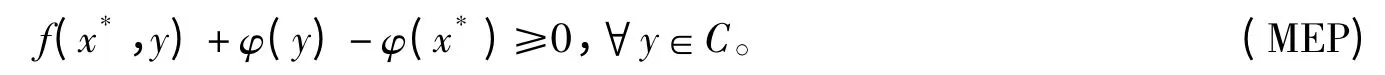
特殊地，若φ=0，问题即简化为古典平衡问题，即寻找x*∈C 使得

设(EP)的解集为Γ，(MEP)的解集为Ω。

近年来，Combettes and Hirstoaga［1］和Moudafi［2］分别在Hilbert 空间中研究寻找非扩张映像或严格伪压缩映像与混合均衡问题解集的公共元素。受此研究成果的启发，文中引入具有显示格式的杂交投影算法，用以逼近严格伪压缩映像的不动点与混合均衡问题解集的公共元，并证明了一个强收敛定理。

1 预备知识

用H 表示实Hilbert 空间，内积和范数为〈·，·〉和‖·‖，F(T)={x∈H|Tx=x}表示映像T 的不动点集。设C⊂H 是非空闭凸子集，记PC∶ H→C 是H 到C 上的投影。用表示序列的“强收敛”。

定义1 称T∶ C→H 是非扩张映像，若对∀x，y∈C，满足

定义2［3］称T∶ C→H 是firmly 非扩张映像，若对∀x，y∈C，满足

定义3［3］称T∶ C→H 是k-严格伪压缩映像，若存在常数0≤k ＜1，对∀x，y∈C 满足

注1 由定义可知，firmly 非扩张映像一定是非扩张的，非扩张映像是0-严格伪压缩的。

设C 为实Hilbert 空间H 的一个非空闭凸子集，f∶ C×C→R 为二元均衡函数。设r 为正数，对于给定的x∈C，所谓均衡问题，即寻找y∈C，使得

式(4)的解集记为EP(f)。

文中二元均衡函数f∶ C×C→R 满足下列条件:

(H4)任意取定x∈C，x→f(x，y)是凸的，且下半连续。

为了证明主要结果，需要下述引理:

引理1［4］设H 是内积空间，对所有∀x，y∈H，t∈［0，1］有

引理2［4］设C 为Hilbert 空间H 中的非空闭凸子集，∀x∈H，∀y∈C，则存在唯一的ω0∈C，满足:(1)ω0=PCx⇔〈ω0-x，y-ω0〉≥0;(2)‖ω0-x‖≤‖y-x‖ 。

引理3［5］设C 为Hilbert 空间H 中的非空闭凸子集，f∶ C×C→R 满足(H1)-(H4)，则对于∀x，y∈H，r ＞0，则存在z∈C，满足

引理4［1］设C 为实Hilbert 空间H 的一个非空闭凸子集，f∶ C×C→R 为二元均衡函数，且满足条件(H1)-(H4)，对∀x∈H，r ＞0，定义映射Sr∶ H→C 为:

则(i)Sr是单值的;

(ii)Sr是firmly 非扩张的，即‖Srx-Sry‖2≤〈Srx-Sry，x-y〉，∀x，y∈H;

(iii)EP(f)是非空闭凸的，且F(Sr)=EP(f)。

2 主要结果

定理:设C 是实Hilbert 空间H 中的非空闭凸子集，且T∶ C→H 为k-严格伪压缩映像，f∶ C×C→R 为二元平衡函数，且满足条件(H1)～(H4)，F=F(T)∩EP(f)≠Φ。序列(un}，{xn}，{yn}及{zn}由下列迭代生成

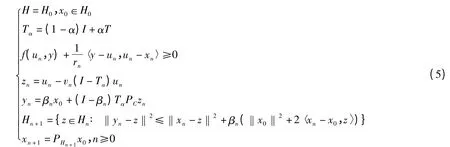
其中vn∈(a，b)⊂(0，1)，βn∈［0，c)c∈(0，1)且，则序列{un}，{xn}，{yn}及{zn}均强收敛于PF(x0)。

证明:第一步:证明Tα∶ C→H 为非扩张映像。

由引理1 及迭代格式(5)，并注意到T 是严格伪压缩映像，

‖Tαx-Tαy‖2≤(1 -α)‖x-y‖2+α［‖x-y‖2+k‖(I-T)x-(I-T)y‖2］-

α(1 -α)‖(I-T)x-(I-T)y‖2=‖x-y‖2+α(α+k-1)‖(I-T)x-(I-T)y‖2。

注意到0 ＜α ＜1 -k，所以

故Tα∶ C→H 为非扩张映像。

第二步:证明F⊂Hn。

由Tα=(1 -α)I+αT 易知F(Tα)=F(T)，故F(Tα)∩EP(f)=F(T)∩EP(f)=F。

由于‖yn-z‖2≤‖xn-z‖2+βn(‖x0‖2+2〈xn-x0，z〉)与〈(1 -βn)xn+βnx0-yn，z〉≤〈xn-yn，等价，故Hn为半空间。∀p∈F =F(Tα)∩EP(f)，由迭代格式(5)及PC和Sr的非扩张性，得

所以p∈Hn。即F⊂Hn，对∀n≥0。

第三步:证明{xn}为柯西列。

由于F(Ta)和EP(f)均是H 的非空闭凸子集，故F =F(Tα)∩EP(f)也是H 的非空闭凸子集。由引理2 知，∀x∈H 存在唯一的ω0∈F(Tα)，使得ω0=PF(Tα)x0。对于固定的正整数m，对∀z∈Hn+m，由‖xn+m-x0‖=‖PHn+mx0-x0‖≤‖z -x0‖知{xn}有界，再借助式(3)知{zn}也有界。由ω0∈F(Tα)⊂Hn+m得，对∀n≥0，‖xn+m-x0‖≤‖ω0-x0‖。由Hn的定义，显然Hn+m⊆Hn，‖xn-x0‖≤‖xn+m-x0‖，对∀n≥0。故存在常数c，使得由引理2 知xn+m∈Hn，xn=PHnx0，且〈xn-x0，xn+m-xn〉≥0，因此‖xn+m-xn‖2≤‖xn+m-x0‖2-‖xn-x0‖2，故所以{xn}为柯西列，即

从而‖xn-un‖2≤‖xn-p‖2-‖un-p‖2，故

移项整理得

∀p∈F，‖xn- p‖≤‖xn- TαPCzn‖ + ‖TαPCzn- p‖≤‖xn- TαPCzn‖ + ‖zn- p‖，移项得‖xn-p‖-‖zn-p‖≤‖xn-TαPCzn‖。由第二步知0≤‖xn-p‖-‖zn-p‖≤‖xn-TαPCzn‖，故

第五步:证明序列{un}，(xn}，{yn}及{zn}均强收敛于PF(x0)。

∀p∈F 由引理1 及迭代格式(5)得

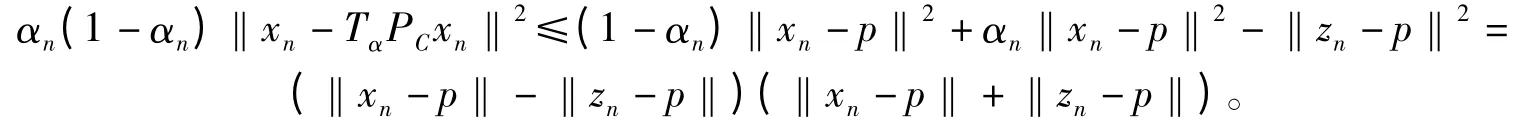
注意到{xn}及{zn}的有界性，得结合式(9)得证明q∈F(Tα)。事实上，由于q=TαPCq，故有PCq =PCTαPCq。由Zhou［6］知，PCq =TαPCq，从而q =PCq，即q∈F(Tα)。再由得q ∈F(Srn)= EP(f)，所以q ∈F(Tα)∩EP(f)=F(T)∩EP(f)=F。即序列{xn}强收敛于PF(x0)。结合式(10)、(11)、(12)知{un}，{yn}及{zn}均强收敛于PF(x0)。

［1］Combettes P L，Hirstoago S A． Equilibrium programming in hilbert spaces［J］． Nonlinear and Convex Analysis，2005，6(5):117-136．

［2］Moudafi A． Second-order differential proximal methods for equilibrium problems［J］． Inequal Pure Appl Math，2003，8(4):1-8．

［3］Bauschke H H，Combettes P L． A weak-to-strong convergence principle for Fejer-monotone methods in Hilbert spaces［J］．Mathematics of Operations Research，2001，26:248-264．

［4］Marino G，Xu H K． Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces［J］． Math． Anal．Appl．，2007，329:336-349．

［5］Takahashi S，Takashi W． Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces［J］． Math． Anal． Appl．，2007，331:506-515．

［6］Zhou H Y． Convergence theorems of fixed points for k-strict pseudo-contraction in Hilbert spaces［J］． Nonlinear Anal．，2008，69:456-462．