一种视频监控图像条纹噪声去除算法

武楠，王珩

（上海海事大学 信息工程学院，上海 200135）

网络、视频通信技术的快速发展和视频监控系统的广泛应用，使得视频图像的分析和内容识别也得到大力推广。因此，如何从视频监控系统中恢复受条纹干扰的帧图像成为人们关注的焦点。同时，图像条纹噪声使一些基于图像识别和目标跟踪等智能化监控受到限制，这些应用大多是基于图像边缘特性分析，条纹噪声干扰给图像的定性和定量分析带来困难，限制了可疑目标的进一步分析。因此，必须寻求合适的条纹噪声去除算法，首先将图像中条纹噪声去除，然后进行分析和比较来保证分析结果的可靠性。由此可知视频图像监控条纹噪声去除算法的研究具有重要意义。

目前，针对图像噪声去除方法的研究，大都是在空间域和变换域进行噪声去除。在空间域中，遥感图领域，结构光条纹领域等有广泛应用，因此很多国内外学者进行了相关的研究。典型的空域横纹噪声消除方法主要有直方图匹配方法[1-2]和矩匹配方法[3]，其中直方图匹配对图像的均匀性要求较高，效果并不理想；而矩匹配方法是应用较为广泛的条纹噪声消除方法，但在景物较复杂时该方法会产生“带状效应”[3]。在变换域中，主要有傅里叶变换、小波变换[4-5]等。傅里叶变换把空间域与频率域联系了起来，将图像变换到频率域，从而利用信号与噪声占有不同的频率成分来进行滤波，达到消除噪声的目的，但是傅立叶变换欠缺对图像局部分析能力。小波变换计算量较大不符合视频监控系统实时性要求。因此将空域和频域有机地结合起来，使信号与噪声在频率域较好地得到分离，取得了较好的噪声去除效果，在去除噪声同时保持图像的纹理细节方面具有较好地平衡。

1 算法原理

1.1 频域滤波

频域滤波是利用图像变换方法将原来的图像空间中的图像以某种形式转换到其它空间中，利用该空间的特有性质方便地进行图像处理，最后再转换回原来的图像空间中，得到处理后的图像。频域滤波技术的基础是傅里叶变换和卷积理论。 假定 g（x，y）表示函数 f（x，y）与线性移不变算子 h（x，y）进行卷积运算的结果：

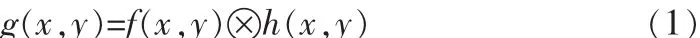
因此可得：

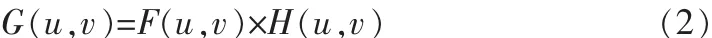
其中 G、F、H 分别是函数 g（x，y）、 f（x，y）、h（x，y）的傅里叶变换。频域滤波方法的系统框图如图1所示，滤波处理过程可分为3步：1）选择变换方法，将输入图像变换到频域空间；2）在频域空间中，根据处理目的设计一个转移函数并进行处理；3）将所得结果用傅里叶逆变换得到滤波图像。

图1 频域滤波系统方框图Fig.1 The frame chart of filtering in frequency domain

1.2 频域累积分布函数映射法

基于傅里叶变换的条纹噪声去除方法中，陷波滤波器参数D0较难确定，前人多是先进行人为地寻找，观察并统计条纹噪声的频率成分和规律。针对这个问题，文中提出了自动寻找频率成分的频域累积分布函数映射法。

对于一幅大小为 M×N的频域图像 F（u，v），设其行列数分别是M和N，其中行方向上的累积分布函数为：

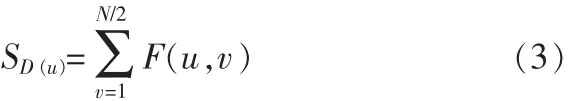
上式计算行方向上的累积分布函数SD（u），计算横纹噪声的频率点即峰值点P，如图2所示。

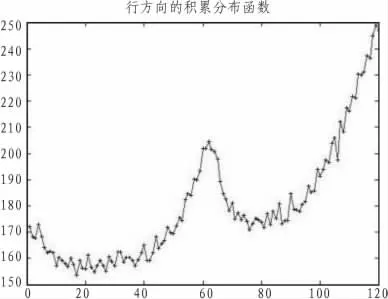
图2 行方向积累分布函数Fig.2 Line orientation distribution function

1.3 图像锐化处理

针对基于傅里叶变换的条纹噪声去除方法会造成对图像边缘的模糊的问题，本算法采用Laplacian算子增强图像的噪声点、细线与边缘，突出图像细节纹理。利用3×3的方向模板与图像中每个点进行邻域卷积来完成，一个二维图像的拉普拉斯Laplacian算子如下。

Δ2f=4f（x，y）-f（x-1，y）-f（x+1，y）-f（x，y-1）-f（x，y+1） （4）

2 算法描述与步骤

去除图像传感器故障引起的等间距横纹噪声的算法大致分为两步，先将帧图像进行傅里叶变换，进行频域滤波处理，其中传递函数选择Butterworth陷波器，运用频域累积分布函数映射法自动寻找横纹噪声频率成分；其次计算去噪图像与Laplacian算子的卷积，得到锐化图像，最后锐化图像与原始图像做图像加法处理，完成横纹噪声去除同时增强图像边缘。

具体的算法步骤描述如下：

1）从当前实时视频图像序列中截取当前一帧图像，对其规格化为320×240并进行灰度变换处理，然后运用公式（5）进行傅里叶变换，得到 F（u，z）。

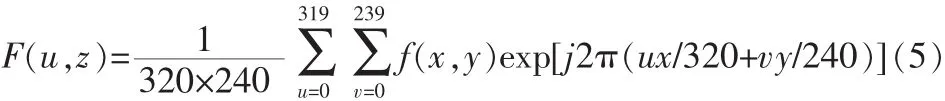
2）构造自适应陷波滤波器H（u，v）。方法如下，实验中利用公式（6）计算幅度谱行方向积累分布函数：

计算横纹噪声的频率点异常峰值P的横坐标T=60，因此可得（u0，v0）=（60，161），选用 2 阶数的巴特沃思陷波滤波器构建自适应滤波器 H（u，v），如公式（7）、（8）、（9）。

3） 运用式（10），（11）对帧图像进行频域滤波处理，传递函数为式（9），得到恢复图像 g（x，y）。

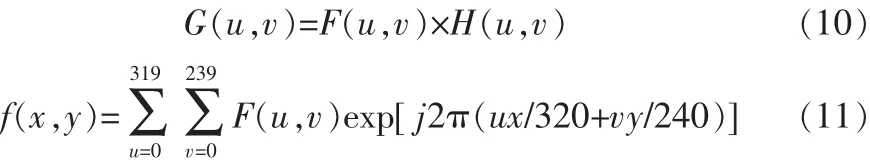
4）通过Laplacian算子与恢复图像g（x，y）进行卷积处理，其中选用Laplacian算子模板，将锐化图像与恢复图像g（x，y）用式（12）图像加法处理，得去除条纹噪声图像f^（x，y）。

3 实验结果与分析

为了验证本算法的有效性，把由720×576分辨率的图像传感器故障引起横纹噪声RGB视频中抽取的横纹帧作为测试样本，实验程序在PC机上运行，先将帧图片规格化为320×240。通过上述的算法原理，得到频率域的噪声点的坐标是 （60，161）。将得到的参数运用到本算法并用传统的低通滤波器、带阻滤波器和陷波滤波器仿真后对比结果如图3所示。

其中（a）图是由于图像传感器故障引起的等间距横纹噪声，（b）图是本算法的条纹去除效果图，（c）Butterworth低通滤波器叠加在原频谱的效果图，（d）Butterworth低通滤波器滤波后的恢复图，（e）Butterworth带阻滤波器叠加在原频谱的效果图 ， （f）Butterworth 带 阻 滤 波 器 滤 波 后 的 恢 复 图 ， （g）Butterworth陷波滤波器叠加在原频谱的效果图，（h）Butterworth陷波滤波器滤波后的恢复图。为了定量的评价各种方法对条纹噪声的消除能力和效果，对图3原图和各滤波后的效果图进行图像质量的评价[6]，即计算方差、均方误差（MSE）、结构相似度[7]（SSIM）和各个图像的列剖面线图 4个评价指标，实验数据如表1所示。

图3 条纹噪声去除的实验结果Fig.3 Experimental results of removing stripe noise

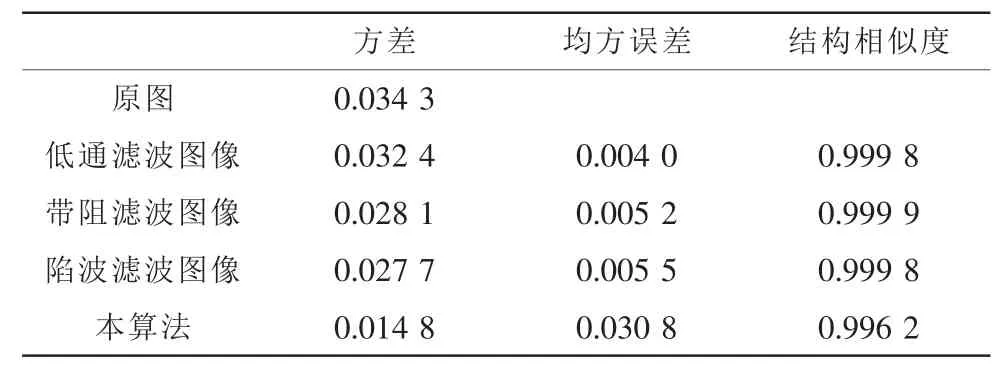
表1 评价指标Tab.1 Index of evaluation

表1中，对于视频监控条纹噪声图像来说，它本身没有标准的原始图像，这里将恢复图作为参考图像用于计算均方误差，由于用的参考图像是恢复图像，所以均方误差值大反而性能好。陷波滤波图像和带阻滤波图像的方差相差不大，表明这两个图像受横纹噪声污染较轻，本算法方差最小，而原图受横纹噪声污染最严重。低通滤波图像的均方误差数最小，这表明它和原图较为接近，即低通滤波去除横纹的性能最差，本算法均方误差数最大说明本算法去除横纹的性能最好。结构相似度评价指标中，本算法的结构相似度最小，说明本算法恢复图与受横纹干扰的原图相似度最小。综上所述，本算法更适合用于图像传感器故障引起的等间距横纹噪声的去除。

4 结束语

文中针对视频图像中图像传感器故障引起的等间距横纹噪声去除问题，提出了基于陷波滤波器的去除条纹噪声算法。首先将视频条纹图进行傅立叶变换，通过频域累积分布函数映射法构造了基于陷波滤波器的自适应滤波器，用得到的滤波器对变换后的条纹图像进行滤波并进行傅里叶逆变换得到恢复图像，最后用Laplacian算子对恢复图像进行锐化处理并与恢复图像叠加，得到最终的去噪图像。实验表明，本算法适合用于去除有图像传感器故障引起的等间距横纹噪声，各种评价指标都高于传统的条纹去噪方法；但此算法的局限性在于只能用于等间距横纹噪声的去除，对其它摄像头干扰或故障引起的斜纹，细纹等条纹不能去除，这也是后续工作的研究重点，使算法的应用更具普遍性。

[1]Hom BKP，Woodham RJ.Destriping landsat MSSimagery by histogram modification[J].Compute Graph&Image Process，1979（10）:69-83.

[2]Kautsky J，Nichols N K，Jupp D L B.Smoothed histogram modification for image processing[J].Compute Vis&Image Process，1984（26）:271-290.

[3]刘正军，王长耀，王成.成像光谱仪条带噪声去除的改进矩匹配方法[J].遥感学报，2002，6（4）:280-284.LIU Zheng-jun，WANG Chang-yao，WANG Cheng.Imaging spectrometer to remove noise bands of improved torque match method[J].Journal of Remote Sensing，2002，6（4）:280-284.

[4]Govani C，Marco D，Thomas W.Striping removal in MOS-B data[J].IEEETransactions on Geoscience&Remote Sensing，2000，38（3）:1439-1446.

[5]罗元俊,叶雪梅,范青刚.离散傅里叶变换和组合能量熵的纹理图像分析[J].电子科技，2011（1）：9-11.LUO Yuan-jun,YE Xue-mei,FAN Qing-gang.Texture image analysis based on discrete fourier transform and permutation entropy[J].Electronic Science and Technology,2011（1）：9-11.

[6]高新波，路文.视觉信息质量评价方法[M].西安:西安电子科技大学出版社，2010.

[7]WANG Zhou，LU Li-gang，Bovik，et al.Video quality assessment based on structural distortion measurement[J].Signal Processing:Image Communication，2004，19（2）:121-132.